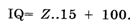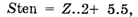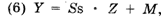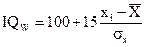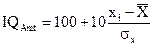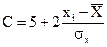Стен оценки — Sten scores
Результаты для некоторых шкал некоторых психометрических инструментов возвращаются в виде оценок sten, причем sten является аббревиатурой от «Standard Ten» и, таким образом, тесно связан с оценками stanine .
Содержание
Определение
Оценка sten указывает приблизительное положение человека (как диапазон значений) по отношению к совокупности ценностей и, следовательно, к другим людям в этой совокупности. Индивидуальные оценки стенограммы определяются со ссылкой на стандартное нормальное распределение. В отличие от оценок станина, у которых средняя точка равна пяти, у оценок стена нет средней точки (средней точкой является значение 5,5). Как и в случае со станнами, баллы по отдельным стенам разграничены половиной стандартного отклонения. Таким образом, оценка 5 по стандарту включает все стандартные оценки от -,5 до нуля с центром -0,25, а оценка по стандарту 4 включает все стандартные оценки от -1,0 до -0,5 и с центром в -0,75. Оценка 1 включает все стандартные оценки ниже -2,0. Стен 6-10 баллов, «зеркало» 5-1. В таблице ниже показаны стандартные баллы, определяющие стены, и процент людей, взятых из нормального распределения, которые получили бы баллы по стенам.
| Z-баллы | +2,0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Процентов | 2,28% | 4,41% | 9,18% | 14,99% | 19,15% | 19,15% | 14,99% | 9,18% | 4,41% | 2,28% |
| Процентиль | 1.14 | 4,48 | 11,27 | 23,36 | 40,43 | 59,57 | 76,64 | 88,73 | 95,52 | 98,86 |
| Стен | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Процентили — это процентиль оценки sten (которая является средней точкой диапазона z-значений).
Баллы Sten (для всей совокупности результатов) имеют среднее значение 5,5 и стандартное отклонение 2.
Подсчет баллов стен
Когда распределение баллов приблизительно нормально распределено, баллы стен могут быть рассчитаны с помощью линейного преобразования: (1) баллы сначала стандартизируются; (2) затем умножается на желаемое стандартное отклонение 2; и, наконец, (3) добавляется желаемое среднее значение 5,5. Полученное десятичное значение можно использовать как есть или округлить до целого числа.
Например, предположим, что установлено, что баллы по шкале имеют среднее значение 23,5, стандартное отклонение 4,2 и приблизительно нормально распределены. Затем Стен баллов по этой шкале можно рассчитать по формуле, . Также обычно бывает необходимо усечь такие оценки, особенно если оценки искажены. ( s — 23,5 ) 4.2 2 + 5.5 <\ displaystyle <\ frac <(s-23.5)><4.2>> 2 + 5.5>
Альтернативный метод расчета требует, чтобы разработчик шкалы подготовил таблицу для преобразования исходных оценок в оценки стен путем распределения процентов в соответствии с распределением, показанным в таблице. Например, если разработчик шкалы замечает, что необработанные оценки 0–3 составляют 2% населения, то эти исходные оценки будут преобразованы в оценку sten, равную 1, а исходная оценка 4 (и, возможно, 5 и т. Д.) Будет преобразуется в оценку стенограммы, равную 2. Эта процедура представляет собой нелинейное преобразование, которое нормализует оценки стенокардии, и, как правило, получаемые в результате стены только приблизительно соответствуют процентным значениям, указанным в таблице. 16-факторный личностный опросник использует этот метод подсчета очков.
Источник
117 iq по шкале стенов
Напомним, что в шкале IQ центр равен 100, а отклонение равно 15.
Если перевод требуется в так называемую шкалу «стенов» (от английского «standard ten» — стандартная десятка), то формула пересчета из шкалы Z выглядит так:
так как в шкале стенов центр равен 5.5, а отклонение равно 2.
Обобщенная формула перевода сырого балла в заданную стандартную шкалу имеет вид:
где У — стандартный балл по произвольной шкале с центром М и отклонением Ss.
Для серьезных профессиональных тестов вместо описанной здесь простейшей линейной стандартизации используется более сложная процедура нелинейной нормализации (форсированный переход к нормальному распределению). В результате этой, более точной, процедуры разработчики снабжают пользователей теста так называемой «КОНВЕРСИОННОЙ ТАБЛИЦЕЙ» для перевода сырых баллов в стандартные баллы по заданной шкале. В ней приводится полный перечень соответствий между интервалами сырой шкалы и интервалами стандартной.
Ниже приведен пример того, как может выглядеть конверсионная таблица для некоторого теста арифметических вычислений из 30 заданий. Простейшая процедура подсчета баллов (за правильный ответ — 1 очко, за ошибку — 0) дает нам сырую шкалу от 0 до 30:
Таблица 1. Пример фрагмента конверсионной таблицы для перевода сырых баллов в стены
| Сырой балл | 0-6 | 7-8 | 8-9 | 10-13 | 14-16 | 17-19 | 20-22 | 23-24 | 25 | 26-30 |
| Стены | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Как пользоваться таблицей? Если испытуемый показал 5 сырых очков (решил только 5 заданий), то ему ставится минимальный стандартный балл 1. Если испытуемый решил 25 заданий, то — балл 9.
Источник
Шкала стенайнов Гилфорда
Тест Амтхауэра
Тест Векслера
Шкала стенов Кеттелла (например, опросники 16 PF Кеттелла, МИС. УСК и т. п.)
Шкала Т-баллов (например, опросники MMPI, CPI, САТ, ГТ и т. п.)
В руководстве по конструированию тестов, принятом Американской психологической ассоциацией, указывается, что типичным преобразованием ненормализованных стандартных показателе (то есть z-показателей) должно быть их приведение к шкале со следующими параметрами: среднее арифметическое 50 (это будет константа b) и стандартное отклонение 10 (константа а).
На рисунке 7 показано соотношение кривой нормального распределения и наиболее распространенных в методиках нормализованных шкал.
Распределение оценок многих стандартизированных педагогических и психологических тестов апроксимируется формой нормальной кривой, показанной в верхней части этого рисунка. Ниже представлены некоторые шкалы, разработанные для упрощения интерпретации оценок путем преобразования их в числа, которые указывают относительное положение тестируемых в группе стандартизации (выборка испытуемых, на которой проводится исследование с целью сбора статистического материала и определения статистической нормы).
Нуль (0) в центре базовой линии показывает положение средней арифметической первичных («сырых») оценок теста, а символ σ(сигма) размечает шкалу «сырых» оценок в
 |
единицах стандартного отклонения.
Накопленные проценты являются основой шкалы «процентильный эквивалент».
Рис. 16. Кривая нормального распределения и тестовые показатели.
Некоторые шкалы основаны на единице стандартного отклонения. Среди этих шкал — стандартная z-оценка, Т-оценка, стены (10-балльная шкала) и стенайны (9-балльная шкала), оценка уровня развития интеллекта IQ — представляют собой шкалы, применяющиеся во множестве тестов.
Таблицы норм, либо в виде процентилей, либо в форме стандартной оценки, имеют значение только для конкретного теста, примененного к определенной выборке стандартизации. Диаграмма не позволяет сделать вывод о том, например, что процентильный ранг 84 по одному тесту обязательно эквивалентен z-оценке +1,0 для другого теста, это справедливо лишь в том случае, когда каждый тест непременно имеет нормальное распределение оценок и когда обе шкалы основаны на идентичных или очень похожих группах людей.
Контрольные вопросы:
1. О чем свидетельствует такой параметр как мода?
2. Методика КОТ (Краткий отборочный тест) позволяет оценить интеллектуальный потенциал человека и принять решение, например, о приеме на работу. В методических указаниях рекомендуется пользоваться медианными нормами. Максимально возможный диапазон значений интеллектуального потенциала в методике от 0 до 50 баллов. О чем свидетельствует значение испытуемого, равное 35, если медиана равна 29?
3. Тест Равенна позволяет получить оценку невербального интеллекта человека как общую сумму баллов по методике (количество правильных ответов по всем сериям). Для интерпретации результата испытуемого в детском варианте методики рекомендуется пользоваться квартилями, полученными на выборке стандартизации (таблицы 10 и 11).
Процентильные нормы для детей 5;5 – 11 лет
(точка с запятой отделяет количество лет от количества месяцев)
| Процентили | Возраст испытуемого(лет; месяцев) | Процентили | |||
| 5;6 | 6;6 | 7;6 | 8;6 | 9;6 | 10;6 |
| – | |||||
| – | – | – |
Примечание: в ячейках таблицы — общее количество баллов по тесту, полученное испытуемым
| Процентили | Уровни | Интерпретация |
| 95 и выше | I | Очень высокий, выдающийся (особо высокоразвитый) интеллект |
| 75 – 94 | II | Незаурядный интеллект |
| 26 – 74 | III | Средний интеллект |
| 6 – 25 | IV | Интеллект ниже среднего |
| 0 – 5 | V | Дефектный (для данного возраста) интеллект |
Например, ребенок 8 лет выполнил задания методики с результатом 23 балла. Какой вывод можно сделать?
4. В методике культурно-свободный тест Кеттелла определяется уровень развития невербального интеллекта человека в единицах IQ. Методические рекомендации содержат возрастно-ориентированные таблицы для перевода IQ в процентили. Если мы видим, что результат испытуемого IQ=115 и это значение соответствует 82-му процентилю, о чем это свидетельствует? Как можно проинтерпретировать данный результат?
5. О чем свидетельствует такой параметр как среднее арифметическое значение?
6. О чем свидетельствует такой параметр как среднее геометрическое значение?
7. О чем свидетельствует такой параметр как среднее гармоническое значение?
8. О чем свидетельствует такой параметр как дисперсия?
9. О чем свидетельствует такой параметр как стандартное отклонение?
10.О чем свидетельствуют такие параметры как коэффициент асимметрии?
11. О чем свидетельствует такой параметр как коэффициент эксцесса?
12. О чем свидетельствует такой параметр как коэффициент вариации?
13. В каких случаях необходимо проверять исходные данные на наличие в них выскакивающих значений?
14. При каких объемах выборок целесообразно проверять первичные данные на наличие в них выскакивающих значений?
15. Что такое нормальный закон распределения?
16. Проанализируйте какой-либо график дифференциального распределения.
17. Что выступает чаще всего в качестве статистической нормы в психодиагностических методиках?
18. Что такое Z-показатели? Каковы основные параметры Z-распределения?

19. Почему необходимо преобразовывать Z-распределение и нормировать Z-показатели?
20. Приведите формулы основных стандартизованных шкал в психодиагностических методиках.
Материалы для изучения темы:
а) основная литература:
1. Ермолаев О. Ю. Математическая статистика для психологов. — М., 2008. — Стр. 43-55.
2. Кутейников А.Н. Математические методы в психологии. – СПб, 2008. — Стр. 15-18; 23-33.
3. Наследов А. Д. Математические методы психологического исследования: Анализ и интерпретация данных. — СПб., 2007. — Гл. 4 (стр. 40-41; 43); гл. 5 (стр. 41-47; 49-62).
4. Сидоренко Е. В. Методы математической обработки в психологии. — СПб.,2004. — Стр. 16-24.
б) дополнительная литература:
1. Ашмарин И. В., Воробьев А. А. Статистические методы в микробиологических исследованиях. — Л., 1962.
2. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии. — М., 1976. — Стр. 30-36; 42-55; 60-61; 76.
3. Суходольский Г. В. Основы математической статистики для психологов. — СПб., 1998. — Стр. 29-57; 80-96.
Тема 4. Статистические гипотезы. Решение задачи сравнения выборок. Параметрические критерии различий
Понятие статистической гипотезы. Проверка гипотез. Нулевая и альтернативная гипотезы. Уровень значимости. Этапы принятия статистического решения. Классификация исследовательских задач, решаемых с помощью статистических методов.
Статистические критерии. Направленная и ненаправленная гипотезы. Таблицы критических значений. Число степеней свободы. Параметрические и непараметрические критерии. Возможности и ограничения параметрических и непараметрических критериев. Уровни статистической значимости. Правило отклонения нулевой гипотезы и принятия альтернативной гипотезы: зона незначимости, зона неопределенности и зона значимости. Мощность критериев. Зависимые и независимые выборки. Общий обзор критериев различий.
Параметрический критерий t Стьюдента для сравнения результатов количественного измерения: назначение критерия, его описание, область применения, алгоритмы его расчета для независимых и зависимых выборок. Поправка Снедекора.
Критерий F Фишера: назначение критерия, его описание, область применения, алгоритмы его применения для независимых и зависимых выборок.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник