Что такое музыкальный фундамент

Куличкин Блог

А это http://petya.blogik.org мой другой блог

Теория музыки для начинающих. Музыкальный строй

Музыкальный строй — одно из базовых, фундаментальных понятий музыкальной теории. С ним связаны такие понятия, как гамма, интервалы, обертоны, консонансы и диссонансы, диезы и бемоли, темперация и хроматизм. Тем не менее, в учебниках по элементарной теории музыкио музыкальном строе пишут кратко и очень туманно. А про интервалы, аккорды и прочее пишут подробно в других разделах. Поэтому нет ничего удивительного в том, что никто не может понять, о чем пишут такие «учебники». Потому что логика нарушается с самого начала. Впрочем, нарушения логики в учебниках теории музыки и путаные рассуждения о музыкальном строе имеют одну природу: многие горе-музыковеды имеют весьма приблизительные знания в области физики и математики. А без физики и математики понять природу звука очень трудно. Не справившись с проблемой музыкального строя, многие «ученые» неудачники пытаются заниматься гармонией, полифонией, анализом музыкальных форм и наступают на те же грабли во второй, третий и четвертый раз. Потому что фундаментом гармонии, полифонии и анализа музыкальных форм является та же самая природа звука.

Сейчас мы займемся исследованием этой природы. Заоблачных знаний по физике и математике нам не потребуется, но калькулятор в соседнем окне советую открыть. Итак. Что такое музыкальный строй? Сейчас разберемся. Для начала, впрочем, нам нужно выучить ноты, поскольку далее мне придется иллюстрировать изложение нотными примерами.

Запишем все ноты подряд: до, ре, ми, ф, соль, ля, си, до, ре, ми, фа и т.д.

Ноты, расположенные в таком порядке, называются гаммой. Гамма может начинаться с любой ноты. Кроме того, гамма может быть не только восходящей (как на картинке), но и нисходящей, например: ми, ре, до, си, ля, соль, фа, ми.

Расстояние между двумя нотами называется интервалом. Расстояние от любой ноты до самой себя называется примой (до-до, ре-ре, ми-ми, фа-фа и т.д.). Интервал между двумя соседними нотами — это секунда (до-ре, ре-ми, ми-фа и т.д.). Расстояние через ноту — терция (до-ми, ре-фа, ми-соль, фа-ля и т.д.). Аналогичным образом определяются интервалы кварта (до-фа, ре-соль, ми-ля, фа-си, соль-до, ля-ре и т.д.), квинта (до-соль, ре-ля, ми-си. ), секста (до-ля, ре-си, ми-до. ), септима (до-си, ре-до, ми-ре, фа-ми. ) и октава (до-до, ре-ре, ми-ми. ). Обращением интервала называется интервал, построенный на тех же нотах, что и данный, но не тождественный данному. Например, обращением терции ре-фа является секста фа-ре (и наоборот).

Интервалы прима и октава отличаются следующим образом. Прима до-до — это расстояние от крайней левой ноты «до» до той же самой крайней левой ноты «до» (на первой добавочной линейке снизу). А октава до-до — это расстояние от крайней левой ноты «до» (на первой добавочной линейке снизу) до ноты «до» восьмой слева (между третьей и четвертой линейками). Октава является обращением примы, прима является обращением октавы.

Теперь представим себя на месте музыкантов, которым понадобилось как-то записать музыку. Записать надо два параметра: высоту звуков и их длительность. О длительностях разговор у нас будет не сегодня, а вот проблема записи высоты. Как записать высоту?

Способы записи были перепробованы разные, но, в конце концов, наиболее практичным оказался способ записи абсолютной высоты. Иными словами, каждой из 13 изображенных на картинке нот должна соответствовать своя частота звука.

Но почему нот всего семь? И почему они начинают повторяться?

Здесь вопрос в том, какую музыку мы будем записывать этими нотами. Музыка в Средние века была преимущественно вокальная. Следовательно, ограничения по высоте во многом определялись диапазоном человеческого голоса. Давайте поэспериментируем. Сколько разных по высоте звуков вы сможете спеть? Теоретически говоря, почти что сколько угодно. Можно плавно завывать (или, по-умному, глиссандировать) начиная от низов диапазона и заканчивая запредельным писком. А если Вы будете петь более-менее осмысленную песню (скажем, «Пусть бегут неуклюже пешеходы по лужам»)? Спев «Пусть бегут. » вы попадете в ноту, которая приходится на слог «неуклюже» с точностью до 1/1000 Герц? Думаю, то вряд ли. Да и не один певец не попадет. Это и не нужно. Достаточно попасть в определенную окрестность ноты, чтобы слушатель понял, что вы спели правильно. То есть, слишком много нот — плохо. «Разметка» голосового диапазона не должна быть слишком частой. Практика показывает, что шкала голосового диапазона обычного человека включает как раз 7-8 делений. В расчете на такие голосовые возможности, в частности, Владимир Шаинский написал песню Крокодила Гены «Пусть бегут неуклюже. ».

Но диапазон профессиональных вокалистов значительно шире. Если попробовать откалибровать такие диапазоны, понадобится 15-20 делений. Почему же тогда нот все-таки именно семь? Неужели раньше не было хороших певцов? Конечно, хорошие певцы были. Дело в том, что не все решал только голосовой диапазон. Была другая причина.

Средневековая музыка была преимущественно церковной. А акустика храмов романского стиля выявляла очень любопытные свойства звука.

Продолжу чуть позже.
Продолжаю 22.31

Если в таком храме спеть так:

То эхо будет примерно таким:

(Внимание. Если эти ноты сыграть на фортепиано — звучание будет приблизительным. Нотами я записал это эхо только для иллюстрации. Таким же приблизительным будет и звучание обертонов на следующей картинке)

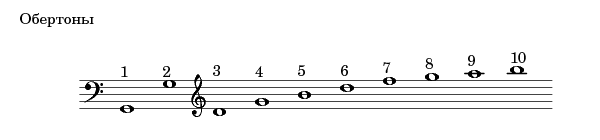
Храмовая акустика усиливала обертоны звука. Что такое обертон? Обертон звука с частотой N — это звук частоты n*N, где n = 1,2,3,4,5. и т.д. Если n=1, то мы получаем первый обертон (т.е. тот же самый основной звук), если n=2 — второй обертон, n=3 — третий обертон и т.д. Приблизительное звучание первых десяти обертонов можно представить, если сыграть на пианино следующее:

Если Вам хочется услышать более точное звучание, тогда предется сделать следующее. Возьмите гитару, которую не жалко, и. плоскогубцы. Сыграйте на открытой струне. Затем зажмите плоскогубцами струну ровно посередине (но так, чтобы натяжение струны не менялось) и сыграйте на половине струны. Это 2-й обертон. Затем зажмите струну так, чтобы можно было сыграть на ее третьей части. Это 3-й обертон. И так далее.

В свое время такой же опыт проделал Пифагор. Он обратил внимание на то, что 2-й обертон очень хорошо сливается с первым. Кроме того, 4-й обертон — это 2-й обертон 2-го обертона, который совпадает со 2-м обертоном так же хорошо, как 2-й с первым. А между 2-м и 4-м обертонами находится третий обертон. Он, конечно, тоже образует красивое созвучие с основным тоном, но не настолько хорошо сливается с ним, как 2-й обертон.

Средневековые музыканты, безусловно, были в курсе исследований Пифагора, и поэтому 2-й обертон они назвали той же нотой, что и основной тон (первый обертон). А поскольку у каждого звука есть свой 2-й обертон, то одни и те же названия нот должны повторяться.

Теперь мы уже можем непосредственно перейти к разговору о том, что же такое, собственно, музыкальный строй. Музыкальный строй — это принцип частотных соотношений между музыкальными звуками. Чтобы создать музыкальный строй, необходимо выбрать количество используемых звуков и установить частотные соотношения между ними. При этом соотношения частот не должны быть произвольными. Они должны соответтвовать природе звука. Иначе музыка в таком строе не будет звучать красиво.

Казалось бы, чего проще? Берем первые 10 обертонов любого звука (см., например, последнюю картинку) и играем на них любые мелодии. Такой принцип тоже использовался. При игре на медных духовых инструментах. Пионерские горны, которые не имеют клапанов, до сих пор так играют. Но песню Крокодила Гены в таком «строе» вы не сыграете. Для вокальной музыки такой принцип подобной организации звуков по частоте не подходит: слишком большой диапазон, слишком редко расположенные звуки внизу и слишком часто расположенные звуки вверху.

Как создать адекватный строй для вокальной музыки (чтобы звуки были расположены более равномерно и в меньшем диапазоне)?

Эту задачу (которая, кстати, называется темперацией) тоже впервые решил Пифагор. Он откалибровал расстояние между 1-м и 2-м обертонам частотами, которые получались умножением или делением частоты основного тона несколько раз на 2 или 3. Например, так. Умножаем частоту основного тона (N) на 2 — получаем второй обертон. Умножаем N на 3 — получаем третий обертон. Он выше, чем второй. Делим 3-й обертон на 2 — получаем звук между 1-м и 2-м обертоном. Это нам подходит. Запоминаем множитель (3/2). Умножаем 3/2N на 3 — получаем очень высокий звук. Выше аж 4-го обертона (действительно, 9/2 > 4). Делим полученную частоту на 2 — получаем звук выше 2-го обертона. Делим еще раз на 2 — попадаем в куда надо, между 1-м и 2-м обертонами. Запоминаем множитель (9/8). Умножаем 9/8N на 3 — опять выше второго обертона. Делим на 2, попадаем между 1-м и 2-м обертонами, запоминаем множитель (27/16). И так далее. Но, кстати. Можно с таким же успехом пойти и в обратном направлении. Умножаем N на 2 и делим на 3. Получаем звук ниже основного тона. Умножаем полученную частоту на 2 — попадаем между 1-м и 2-м обертонами, запоминаем множитель(4/3).В итоге получится что-то вроде:

Около нот подписаны множители. Таким способом теоретически можно «втиснуть» любое количество нот между 1-м и 2-м обертонами. На практике, однако, количество оказывается отнюдь не любым. Спеть с какой угодно точностью все равно не получится. Но здесь, возможно, даже это не главное. Главное, что чем больше знаменатель дроби, тем труднее точно выстроить ноту. Нота си (крайняя справа) выстраивается настолько трудно, что это практически нереально. В самом деле, попробуйте взять линейку, разделить гитарную струну на 243 части, а затем отмерять плоскогубцами 128 частей и этих 243-их. Нота ми, впрочем, выстраивается не намного легче: отмерять 64 раза по одной 81-й тоже то еще удовольствие.

В итоге остаются ноты до, ре, фа, соль и ля. Это так называемая пентатоника. Что-то подобное использовалось (а может быть, и используется) в китайской народной музыке (об этом мы поговорим, когда будем рассматривать лады).

Но вернемся к настройке по квинтам. Самое главное, что сейчас нам уже удалось заполнить расстояние между 1-м и 2-м обертонами семью нотами. Конечно, у нас получились плохо настраиваемые ноты ми и си, но это нетрудно поправить. Нотой си можно обозначить другой звук, с частотой 16/9N, а вместо ми — звук с частотой 32/27N. Делить струну на 32 и 16 все-таки легче, чем на 243 и 81. На практике, впрочем, седьмая нота появилась далеко не сразу. Относительно долгое время обходились шестью нотами (без си). Или, если в другом варианте, без частоты 32/27N.

Семь нот легко выстроить, если использовать так называемый чистый строй. Зачем понадобился чистый строй? Неужели столь необходимой оказалась седьмая нота? Вряд ли. Просто в пифагоровском строе обнаружился один весьма заметный изъян.

Продолжу завтра.
Продолжаю.
27.10.2009
18.27

Этот изъян обнаружился, когда музыка стала многоголосной. А именно, «грязновато» звучали одновременные терции. Например, если один поет ноту до с частотой N, а другой — ноту ми с частотой 81/64N (т.е. выстроенную пифагоровским способом), это будет звучать несколько фальшиво. Почему? Четвертый обертон ноты ми — с частотой 81/16N, а пятый обертон ноты до будет звучать с частотой 5N=80/16N. Если разделить большую частоту на меньшую, получим разницу 81/80. Если у Вас есть две гитары и плоскогубцы, попробуйте сыграть одновременно на двух струнах, одна из которых длиной 81 см, а другая 80 см. Это весьма существенная фальшь, даже с учетом того, что четвертый и пятый обертоны звучат гораздо тише основного тона. Они быстро гасят друг друга, если спеть вначале до, а потом ми. Но когда ми и до звучат одновременно, несовпадающие обертоны «вступают в конфликт». Решить проблему можно так. Ноты ре, фа и соль настраиваем старым, пифагоровским способом. А ноты ми, ля и си — по-новому, с использованием 5-го обертона. Ищем 5-й обертон ноты до — частота 5N. Это очень высоко. Спускаемся на две октавы (делим частоту на 4), попадаем в зону между 1-м и 2-м обертонами, запоминаем множитель (5/4). Ищем пятый обертон ноты фа — 20/3N. Спускаемся на две октавы, запоминаем множитель (5/3). Ищем пятый обертон ноты соль — 15/2N. Спускаемся на две октавы, запоминаем множитель (15/8). Получаем вариант чистого строя:

Рассмотрим некоторые свойства пифагоровского и чистого строев.

• В сравнении с пифагоровским, знаменатели дробей-множителей гораздо меньше. Наибольший из них равно восьми. Выстроить семь нот в чистом строе гораздо легче;
• В обоих строях идентичны квинты: до-соль, ми-си, фа-до (отношение большей частоты к меньшей =3/2). Квинта ре-ля в чистом строе не совпадает с вышеперечисленными (отношение частот = 40/27);
• Кварты до-фа, ре-соль, ми-ля, соль-до также идентичны как в пифагоровском, так и в чистом строе (отношение частот =4/3). Кварта ля-ре в чистом строе не совпадает с ними (отношение частот = 27/20);
• Терции до-ми, фа-ля, соль-си идентичны в обоих строях, но с разными отношениями (5/4 в чистом строе, 81/64 в пифагоровском);
• Терции ре-фа, ми-соль, ля-до, си-ре идентичны в пифагоровском строе (отношение 32/27). В чистом строе идентичны только терции ми-соль, ля-до и си-ре (отношение 6/5), а «пифагоровская» терция ре-фа (32/27) неидентична им;
• Кварта фа-си не совпадает с другими квартами в обоих строях. Отношения частот этого интервала 729/512 в пифагоровском и 45/32 в чистом строе;
• Квинта си-фа не совпадает с другими квинтами. Отношение частот — 1024/729 в пифагоровом и 64/45 в чистом строе;
• Секунды до-ре, фа-соль, ля-си идентичны в обоих строях (отношение частот 9/8);
• Секунды ми-фа и си-до идентичны в обоих строях (отношение 16/15);
• Секунды ре-ми и соль-ля идентичны секундам до-ре, фа-соль и ля-си в пифагоровом строе, но неидентичны в чистом (отношение 10/9);
• Идентичность/неидентичность секст и септим в обоих строях соответствует идентичности/неидентичности терций и секунд, построенных на тех же самых нотах.

Перерыв на ужин.
Продолжаю.
21.00

Что следует из всего этого? Очень многое.

1 О Кварты и квинты почти все идентичны, а терции, секунды, сексты и септимы встречаются в двух разновидностях. Терции ре-фа, ми-соль и си-ре более узкие, чем до-ми, фа-ля и соль-си (поскольку 32/27 16/15, 10/9 > 16/15). Поэтому чтобы отличить более широкие терции и секунды от более узких их стали называть большими и малыми. Большие терции: до-ми, фа-ля, соль-си. Малые терции: ре-фа, ми-соль, ля-до, си-ре. Большие секунды: до-ре, ре-ми, фа-соль, соль-ля, ля-си. Малые секунды: ми-фа, си-до. Малые и большие сексты и септимы при желании вы можете выписать самостоятельно. Обратите внимание: обращением большой секунды (терции) является малая септима (секста). А кварты и квинты (за исключением кварты и квинты на нотах фа и си), а также, октава и прима называются чистыми.

2 О Чем больше знаменатель дроби, выражающей отношение частот, тем выше диссонантность интервала. К тому, что «разница между консонансом и диссонансом не качественная, а количественная» (А. Шёнберг), музыкально-теоретическая мысль пришла только в XX веке. До этого момента одни интервалы считались консонансами, а другие — диссонансами. При этом консонансы подразделялись на совершенные и несовершенные. В музыкальных школах и училищах до сих пор учат, что октава, квинта и кварта — совершенные консонансы, сексты и терции — несовершенные консонансы, а все остальные интервалы — диссонансы. Почему так считалось когда-то? Действительно, у октавы отношение частот =2/1. Знаменатель равен единице. У квинты отношение частот =3/2. Знаменатель =2. У кварты — 4/3, знаменатель =3. У большой терции в чистом строе 5/4 (знаменатель 4), а в пифагоровом — 81/64 (знаменатель 64). У малой терции в чистом строе 6/5 (знаменатель 5), а в пифагоровом — 32/27 (знаменатель 27). Поэтому при использовании пифагоровского строя терция считалась диссонансом, а позднее, когда появился чистый строй, стала консонансом. Правда, в чистом строе осталась «неправильная» диссонирующая пифагоровская терция ре-фа. Секунды во всех строях считались диссонансами. Наименьший знаменатель у секунд — 8 (для больших секунд в обоих строях), наибольший — 15 (для малых секунд в обоих строях). Самыми диссонирующими интервалами из всех вышеперечисленных являются неидентичные кварта и квинта. Их отношения частот (45/32 и 64/45 в чистом, 729/512 и 1024/729 в пифагоровском) говорят сами за себя. Поэтому неидентичную кварту назвали увеличенной (729/512> 4/3, 45/32 > 4/3), а неидентичную квинту — уменьшенной (1024/729 О В чистом строе интервалы легче выстроить, чем в пифагоровском (потому что меньше знаменатели множителей частот). Но в чистом строе есть «аномальная» пифагорова терция ре-фа и «аномальные» пифагоровы секунды ре-ми и соль-ля. А самое главное, в чистом строе появились «плохие» квинта и кварта на нотах ре и ля. Интервалы в чистом строе менее универсальны, чем в пифагоровском. Может ли это привести к проблемам? Может, причем к проблемам очень серьезным. Но заметными такие проблемы могут стать только в инструментальной музыке.

4 О Чистая кварта — особый интервал. Как вы помните, мы ее строили, шагая как бы «в обратном направлении». В одних условиях она считалась диссонансом, а в других — консонансом. Этот разговор отложим до тех времен, когда разговор пойдет о гармонии или полифонии.

Но об этом, надеюсь, поговорим завтра.

28.10.2009
16.13

Если у вас хороший слух или хорошая математическая интуиция, вы, вероятно, уже догадались, что в многоголосии уменьшенная квинта и увеличенная кварта принесут много проблем. Так и случилось. Семи нот стало не хватать. Почему? Вернемся чуть назад:

Но ведь аналогичное эхо можно услышать и от других нот: от ре, ми, фа, соль, ля, си. И среди первых пяти обертонов этих нот появятся новые звуки:

Не совпадают с уже выстроенными нотами пятые обертоны нот ре, ми, ля и два обертона ноты си: третий и пятый. Конечно, если использовать пифагоров строй и считать терцию диссонансом, на несовпадающие пятые обертоны можно закрыть глаза. Тем более, что в пифагоровском строе третий обертон ноты си не совпадает с пятым обертоном ноты ре, хоть и довольно близок к нему. Однако от третьего обертона ноты си никуда не денешься как в чистом, так и в пифагоровском строе.

Попробуем вычислить частотные множители этих новых нот так, чтобы они «попадали» между первым и вторым обертонами ноты до. 5-й обертон ноты ре (9/8 в обоих строях) — 45/8. Делим частоту на 4, чтобы попасть между 1-м и 2-м обертонами до — получаем множитель 45/32. Запоминаем. 5-й обертон ноты ми (81/64 в пифагоровском, 5/4 в чистом строе) — 405/64 и 25/4 в пифагоровском и чистом строях соответственно. Делим на 4 — получаем соответственно 405/256 и 25/16. Вычисляем множитель 5-го обертона ноты ля, делим его частоту на 8, получаем 25/24 для чистого и 135/128 для пифагоровского строев. Аналогично поступаем с 5-м обертоном ноты си: 75/64 для чистого, 1215/1024 для пифагоровского строев. 3-й обертон ноты си — 45/8 для чистого и 729/128 для пифагоровского строев. Делим на 4, получаем для чистого и пифагоровского строев соответственно 45/32 и 729/512.

На картинке эти звуки обозначены теми же самыми нотами, но с диезами. Почему теми же нотами? Как говорят математики, по построению. От нот до, фа и соль у нас строятся большие терции. От нот ре, ми, ля и си — малые. Новые звуки, построенные с использованием 5-х обертонов ре, ми, ля и си образуют с ними точно такие же большие терции, как до-ми, фа-ля и соль-си. А ноты фа-диез (45/32), соль-диез (405/256 и 25/16), до-диез (135/128 и 25/24) и ре-диез (1215/1024 и 75/64) звучат выше, чем фа (4/3), соль (3/2), до (1) и ре (9/8) соответственно. Поэтому диез перед нотой — знак повышения. А интервалы, в которых участвуют ноты с диезами или бемолями (о бемолях речь впереди) называются хроматическими.

Малые секунды ми-фа и си-до, как было показано ранее, идентичны в обоих строях. Совпадают ли с ними малые секунды до-диез-ре, ре-диез-ми, фа-диез-соль и соль-диез-ля? Давайте проверим. Отношение частот секунд ми-фа и си-до в обоих строях =16/15. «Новые» малые секунды в пифагоровском строе совпадают со старыми. А в чистом строе появляется «плохая» малая секунда до-диез-ре с отношением частот =27/25.

Теперь давайте вычислим отношения частот увеличенных прим для пифагоровского и чистого строев:

до-до-диез: 135/128 и 25/24

ре-ре-диез: 135/128 и 25/24

фа-фа-диез: 135/128 и 135/128

соль-соль-диез: 135/128 и 25/24

Надо заметить, что пифагоровский строй с диезными нотами, которые мы только что вычислили с использованием 5-го обертона, уже не является пифагоровским. Просто потому, что пифагоровский строй исключает использование 5-го обертона.

И теперь мы пришли к противоречию. Допустим, мы подстраиваем ноты с диезами к пифагоровому строю и получаем «гибридный» строй с одинаковыми интервалами. Но тогда мы не можем чисто выстроить большие терции до-ми, фа-ля и соль-си (и они будут неидентичны большим терциям с диезами). А если мы чисто выстраиваем терции без диезов, тогда у нас появятся неидентичные секунды и терции.

Что хуже: «плохие» большие терции или неидентичные интервалы? Вопрос риторический. Одно может быть более приемлемо, чем другое в зависимости от конкретного музыкального контекста. В хоровой музыке без аккомпанемента можно легко перестроиться с чистого строя, скажем, на «гибридный» и наоборот. Но если нам нужно, чтобы хору аккомпанировал орган, то его лучше настроить раз и навсегда (поверьте, настройка органа — не самая легкая задача).

NB! К слову сказать, идентичные интервалы очень желательны для того, чтобы можно было использовать разные тональности. Но разговор о тональности мы пока что отложим.

И обратим внимание вот на что:

1. У нас есть теперь одиннадцать звуков, обозначенных просто нотами (7) и нотами с диезами (4). Между этими нотами образуются 10 чистых квинт с отношением частот 3/2. Эти квинты могут быть построены от любого из 11 звуков как вверх, так и вниз, за двумя исключениями. От ноты фа квинта можно построить только вверх. От ноты ре-диез — только вниз;
2. «Шкала высоты» между первым и вторым обертонами у нас проградуирована почти равномерно: каждая большая секунда поделена на увеличенную приму и малую секунду. Кроме большой секунды ля-си. Там, собственно, и находятся недостающие квинты.

Построим квинту вверх от ре-диеза. Это будет звук ля-диез. Его частотный множитель =225/128 для чистого строя, 3645/2048 для «гибридного строя» (ля-диез можно выстроить в чистом строе и с использованием 5-го обертона ноты фа-диез, множитель =225/128).

Теперь построим кварту вверх от фа. Это будет звук си-бемоль (с частотным множителем 16/9). Он ниже, чем си (16/9 2 /125 2 . Это огромный интервал, почти равный малой секунде (16/15)!

Может быть, следует отказаться от подстройки терции и вернуться к пифагоровской настройке исключительно по квинтам? Увы, это тоже не решит проблемы:

Ноты си-диез и ре-дубль-бемоль стали ближе к ноте до, но все равно не тождественны ей.

Похоже, что настроить 12 звуков так, чтобы все квинты и терции звучали чисто, невозможно в принципе. Более того, даже си-бемоль, настроенный по 3-му обертону, будет «конфликтовать» с 7-м обертоном:

Си-бемоль, выстроенный по квинтам имеет частотный множитель =16/9. А си-бемоль, настроенный по 7-му обертону — множитель =7/4. Все равно идеальной чистоты достичь не удастся. А ведь седьмым обертоном ряд не заканчивается.

Поэтому возникла идея равномерной темперации. Она заключается в следующем. Расстояние между 1-м и 2-м обертонами делится на 12 равных частей. При этом до-диез=ре-бемоль, ре-диез=ми-бемоль, фа-диез=соль-бемоль, соль-диез=ля-бемоль, ля-диез=си-бемоль. Идентичными станут любые интервалы с однаковым названием. Кроме того, уменьшенная квинта станет идентичной увеличенной кварте, увеличенная прима — малой секунде и т.д. В равномерно-темперированном строе мы може записать следующие хроматические гаммы:

На картинке вверху подписаны множители. Чтобы получить частоту ноты до-диез или ре-бемоль, необходимо умножить частоту ноты до на величину x (которую мы сейчас найдем). Чтобы получить частоту ноты ре, исходную частоту надо умножить на х два раза.Чтобы получить ре-диез (ми-бемоль) — три раза. И так далее. Чтобы получить 2-й обертон, частоту основного тона нужно умножить на x 12 раз. Записываем уравнение:

x 12 =2

И, решая его, находим x:

x=2 1/12

Остается, разве что, поговорить о проблемах хорового строя. Но об этом лучше поговорить отдельно.

Комментарии:

Юра
27.10.2009 22:14

Интересно, а можно где-то послушать вот это все? Как это все звучит. Или только писать программу, которая будет генерировать звуки заданных частот?

kgv
28.10.2009 23:57

Где же взять столько математиков среди музыкантов и столько музыкантов среди математиков? Не значит ли это, что музыкальную грамоту необходимо начинать внедрять в системе начального образования в рамках общеобразовательного стандарта, как это делают, если мне не изменяет память, в Венгрии и Японии? Детские мозги более податливы на знания.

Юра
27.01.2010 14:18

В процессе обсуждения с другими интересующимися произошел некоторый затык с Пифагоровским строем.

Вот там у Пифагора получилось, вроде бы, достаточно красиво и логично: если строить ноты квинтами от до, то частота верхней ноты квинты равна 3/2 частоты нижней, т.е. верхняя нота квинты — это третий обертон нижней ноты, сдвинутый на октаву вниз.

Но. Построение, почему-то, начинается фактически с фа (значение 4/3), а не с до (значение 1). Так что «корявой» остается нота си (от которой вверх квинта получается кривая).

Как-то непонятно. Почему нота фа строится не от си вверх, как логично ожидать, а от до вниз. Опять какая-то сегрегация непонятная.

petya Читать все комментарии petya
27.01.2010 18:57

Можно и от си верх, но это будет нота, которая соответствует фа-диезу. Вы рассуждаете совершенно верно. Можно по квинтам строить и от до, а вместо фа (множитель 4/3) использовать фа-диез (множитель 729/512). Но 729/512 — это ведь гораздо более «корявая» дробь, чем 4/3! А Пифагор как раз таки отмечал, что чисто и красиво звучат интервалы, если у них маленькие множители.

Поэтому задача заключалась как раз в том, чтобы найти семь нот с такими множителями, чтобы это было оптимально. Конечно, аналогично, вместо си (243/128) можно использовать си-бемоль (16/9), и так далее. Чем больше нот, тем больше появляется «корявых» множителей. Именно из-за этого поначалу использовалось пять нот, потом шесть, а уже потом семь.

А по поводу того, какой строй лучше, пифагоров или чистый — народ спорил около 700 лет, и так, по большому счету, ничего и не наспорил :-))

Алексей Хохлов
25.08.2010 17:26

Петя, зачем плоскогубцами гитару мучить предлагаешь? Достаточно пальцем прикоснутся слегка к струне, не прижимая струну к грифу — и сразу убрать палец после извлечения звука, чтобы не глушил.

petya Читать все комментарии petya
25.08.2010 17:40

Да, согласен. Хорошую гитару плоскогубцами мучить нельзя. Однако пальцем зажимать и потом отпускать — это ж ловкость рук нужна. А если нету таковой, а есть плоскогубцы и некая конструкция из дерева и проволоки, которую, тем не менее, некоторые люди все-таки называют гитарой? Как в этом случае быть? ))

Источник