Расчёт конечной осадки фундамента методом эквивалентного слоя
Эквивалентным называется слой грунта мощностью hэ, осадка которого при сплошной нагрузке на поверхности pо будет равна осадке грунтового полупространства под воздействием местной нагрузки интенсивностью ро.
Осадка слоя грунта из условия одномерного сжатия без возможности бокового расширения 
где Е – модуль деформации грунта; v – коэффициент Пуассона.
Значение v принимаются в зависимости от вида и состояния грунтов:
— глины и суглинки твёрдой и полутвёрдой консистенции v = 0,1…0,15;
— то же тугопластичной v = 0,2…0,25;
— то же мягко пластичной и текучепластичной v = 0,3…0,4;
— то же текучей v = 0,45…0,5;
С учётом относительного коэффициента сжимаемости грунтов mv
β – коэффициент, зависящий от коэффициента Пуассона, т.е.

Толщина эквивалентного слоя hэ =Aωb, (6.5)
где: А– площадь подошвы фундамента; ω – коэффициент, зависящий от формы, площади и жёсткости фундамента, значения табулированы в табл. 3.
Значения коэффициентов ω для полупространства
| Отношение сторон n=ℓ/b | ωс | ωо | ωm | ωсоnst |
| 1-круг | 0,64 | 1,00 | 0,85 | 0,79 |
| 1-квадрат | 0,5 ωо | 1,12 | 0,95 | 0,88 |
| 2-прямоугольник | 0,5 ωо | 1,53 | 1,30 | 1,22 |
| 3- прямоугольник | 0,5 ωо | 1,78 | 1,53 | 1,44 |
| 4- прямоугольник | 0,5 ωо | 1,96 | 1,70 | 1,61 |
| 5 – прямоугольник | 0,5 ωо | 2,10 | 1,83 | 1,72 |
| 10 — прямоугольник | 0,5 ωо | 2,53 | 2,25 | 2,12 |
ωс – для осадки угловой точки прямоугольника или круга;
ωо – для максимальной осадки гибкого фундамента под центром загружаемой площади;
ωm – для средней осадки гибкого фундамента всей площади загружения;
ωсоnst – для осадки абсолютно жёстких фундаментов.
b – ширина подошвы фундамента.
Произведение Aω называется коэффициентом эквивалентного слоя, значения табулированы в табл. 4.
Значения коэффициента эквивалентного слоя Aω
| Соотнош. ℓ / b | Гравий и галька | Пески | Суглинки пластичные | Глины и суглинки мягкопластичные | ||||||||||||||
| Глины и суглинки твёрдые и полутвёрдые | Супеси твёрдые и пластичные | Глины пластичные | ||||||||||||||||
| v = 0,10 | v = 0,20 | v = 0,25 | v = 0,30 | v = 35 | v = 40 | |||||||||||||
| 1,0 | 1,13 | 0,96 | 0,89 | 1,20 | 1,01 | 0,94 | 1,26 | 1,07 | 0,99 | 1,37 | 1,17 | 1,08 | 1,58 | 1,34 | 1,24 | 2,02 | 1,71 | 1,58 |
| 1,5 | 1,37 | 1,16 | 1,09 | 1,45 | 1,23 | 1,15 | 1,53 | 1,30 | 1,21 | 1,66 | 1,40 | 1,32 | 1,91 | 1,62 | 1,52 | 2,44 | 2,07 | 1,94 |
| 2,0 | 1,55 | 1,31 | 1,23 | 1,63 | 1,39 | 1,30 | 1,72 | 1,47 | 1,37 | 1,88 | 1,60 | 1,49 | 2,16 | 1,83 | 1,72 | 2,76 | 2,34 | 2,34 |
| 3,0 | 1,81 | 1,55 | 1,46 | 1,90 | 1,63 | 1,54 | 2,01 | 1,73 | 1,62 | 2,18 | 1,89 | 1,76 | 2,51 | 2,15 | 2,01 | 3,21 | 2,75 | 2,59 |
| 4,0 | 1,99 | 1,72 | 1,63 | 2,09 | 1,81 | 1,72 | 2,21 | 1,92 | 1,81 | 2,41 | 2,09 | 1,97 | 2,77 | 2,39 | 2,26 | 3,53 | 3,06 | 2,90 |
| 5,0 | 2,13 | 1,85 | 1,74 | 2,24 | 1,95 | 1,84 | 2,37 | 2,07 | 1,94 | 2,58 | 2,25 | 2,11 | 2,96 | 2,57 | 2,42 | 3,79 | 3,29 | 3,10 |
| 6,0 | 2,25 | 1,98 | — | 2,37 | 2,09 | — | 2,50 | 2,21 | — | 2,72 | 2,41 | — | 3,14 | 2,76 | — | 4,00 | 3,53 | — |
| 7,0 | 2,35 | 2,06 | — | 2,47 | 2,18 | — | 2,61 | 2,31 | — | 2,84 | 2,51 | — | 3,26 | 2,87 | — | 4,18 | 2,67 | — |
| 8,0 | 2,43 | 2,14 | — | 2,56 | 2,26 | — | 2,70 | 2,40 | — | 2,94 | 2,61 | — | 3,38 | 2,98 | — | 4,32 | 3,82 | — |
| 9,0 | 2,51 | 2,21 | — | 2,64 | 2,34 | — | 2,79 | 2,47 | — | 3,03 | 2,69 | — | 3,49 | 3,08 | — | 4,46 | 3,92 | — |
| 10 и более | 2,58 | 2,27 | 2,15 | 2,71 | 2,40 | 2,26 | 2,86 | 2,54 | 2,38 | 3,12 | 2,77 | 2,60 | 3,58 | 3,17 | 2,98 | 4,58 | 4,05 | 3,82 |
| Коэфф. | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst |
Для однородного основания требуемая осадка при известных E и ν определяется по формуле (6.2).
Для слоистого основания осадка

где: mv – средневзвешенный относительный коэффициент сжимаемости

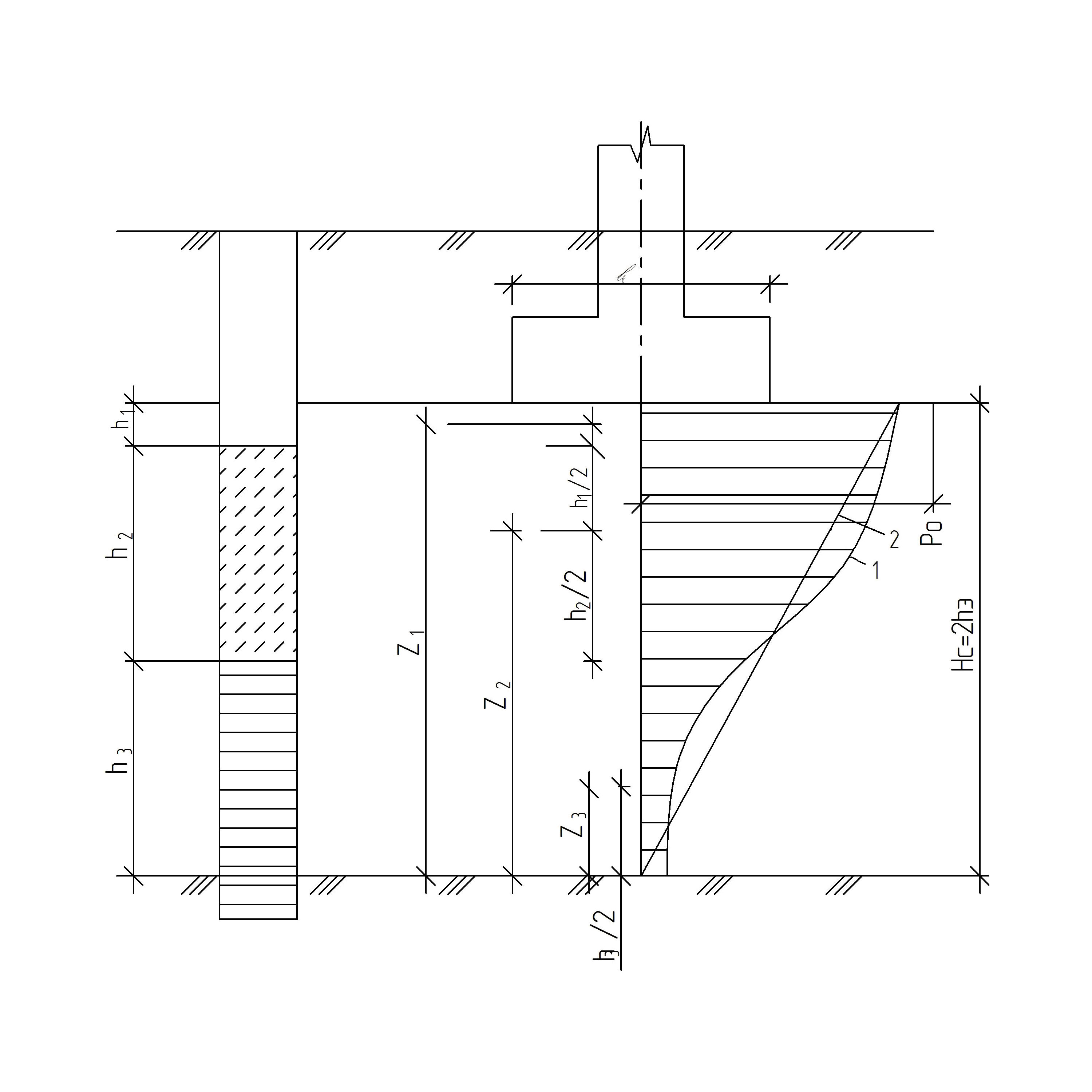
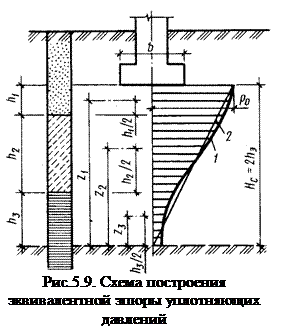
который определяется с использованием расчётной эпюры на рис. 14.
Рис. 14. Схема к определению осадок методом эквивалентного слоя для многослойного основания:
1 – расчётная нелинейная эпюра дополнительных напряжений;
2 – эквивалентная треугольная эпюра дополнительных напряжений.
Средневзвешенное значение коэффициента Пуассона

где Нс – мощность сжимаемой толщи основания
Пример расчёта:
Определить методом эквивалентного слоя осадку столбчатого фундамента, рассчитанного в п.п. 6.1 и 6.2,
Р о = Р — 
Грунтовые условия – по заданию.
II слой – песок мелкий, средней плотности с коэффициентом Пуассона ν=0,2.
При глубине заложения фундамента 3,05 м
h = 5.5 – 3.05 = 2,45 м
По табл. 4 определяем Аωm=1,01.
Толщина эквивалентного слоя
Мощность сжимаемой толщи
При глубине заложения подошвы фундамента d=3,05 м в сжимаемую толщу входит II и III слои грунтов с модулями деформаций ЕI I =28 МПа,
Относительные коэффициенты сжимаемости для:
— второго слоя при νI I = 0,2; 

— третьего слоя ( глина пылеватая, комковая, полутвердая)
νI I I = 0,12; 
— средний относительный коэффициент сжимаемости
Конечная осадка фундамента

Источник
Расчет осадок фундаментов методом эквивалентного слоя
Разработанный Н.А.Цытовичем метод эквивалентного слоя дает возможность для многослойных оснований существенно упростить расчет конечных осадок и развитие осадок во времени (пример 10).
Эквивалентным слоем грунта hэ называется слой, осадка которого S0 при сплошной нагрузке равна осадке фундамента Sn на мощном массиве при местной нагрузке на полупространстве:
Выше было установлено, что при сплошной нагрузке относительная деформация слоя грунта
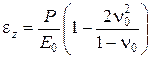
Умножая эту величину на полную высоту слоя hэ, получим
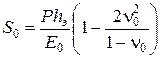
Осадка реального фундамента на мощном массиве грунта или слое грунта ограниченной мощности
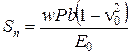
Подставляя в выражение (5.27) значения (5.28) и (5.29) и решая уравнения относительно hэ, получаем
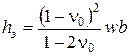
Если постоянный коэффициент обозначим одним символом
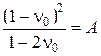
то получим формулу для определения мощности эквивалентного слоя грунта
где b – ширина фундамента.
Из формулы (5.31) видно, что мощность эквивалентного слоя грунта зависит от бокового расширения грунта (коэффициент А), от формы и жесткости фундамента (коэффициент w) и пропорциональна ширине фундамента.
С учетом (5.31) получим формулу для определения осадки фундамента заданных размеров:
Значения коэффициента эквивалентного слоя Aw табулированы для определения максимальных, средних осадок гибких фундаментов (Aw0, Awm) и осадок абсолютно жестких фундаментов (Awconst) в зависимости от отношения сторон фундамента l/b и коэффициента Пуассона n0 (табл.IV.4, IV.5 приложения IV).
Следует отметить, что соотношение между коэффициентами для круглых и квадратных фундаментов
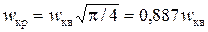
Между коэффициентами эквивалентного слоя для центра прямоугольной площади абсолютно гибкой нагрузки и ее угловой точки существует простое соотношение
Awc – коэффициент эквивалентного слоя для угловой точки.
5.3.6. Метод угловых точек. Учет взаимовлияния фундаментов
Для определения осадок фундаментов с прямоугольной площадью подошвы, определения осадки в любой точке за пределами загруженной площади, взаимовлияния фундаментов пользуются методом угловых точек (см. раздел 3) (пример 11).
 |
При определении осадки по методу угловых точек рассматриваемую точку располагают так, чтобы она была угловой. В этом случае осадка любой точки поверхности грунта под действием равномерно распределенной нагрузки равна сумме осадок грунта от прямоугольных площадей загрузки, для которых эта точка является угловой.
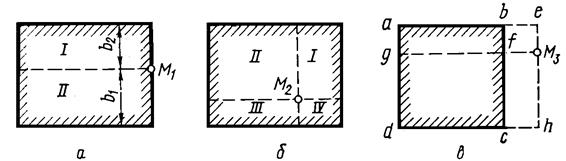
Рис.5.7. Схемы построения прямоугольников загрузки при определении
осадок по методу угловых точек
На рис.5.7 показаны три основных случая:
1. Точка М1 лежит на контуре загруженного прямоугольника (а). Осадку точки М1определяем как сумму осадок угловых точек прямоугольников I и II:
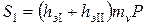
где 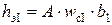
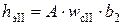
2. Точка М2 лежит внутри загруженного прямоугольника (б). В данном случае загруженную площадь разбиваем на четыре прямоугольника так, чтобы точка М2оказалась угловой. Осадка точки М2будет
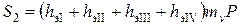
где hэi – толщина эквивалентного слоя для соответствующих площадей загрузки.
3. Точка М3лежит вне загруженного прямоугольника (в). В этом случае осадка складывается из суммы осадок угловых точек прямоугольников загрузки I =+ aеM3q; II =+ qM3hd; III = — bеM3f; IV = — fM3hc:
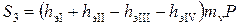
Мощность каждого эквивалентного слоя hэi определяется по формуле
где Awc – коэффициент эквивалентного слоя, принимаемый по таблицам в зависимости от отношения сторон рассматриваемого прямоугольника и коэффициента Пуассона (табл.IV.5 приложения IV).
Метод угловых точек дает возможность учесть разность осадок различных фундаментов и взаимовлияние смежных фундаментов.
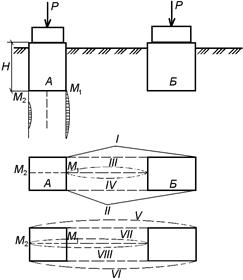
Схема на рис.5.8 позволяет учесть влияние вновь возводимого фундамента Б на существующий фундамент А. В результате такого влияния фундамент А накреняется в сторону фундамента Б.
Рис.5.8. Схема использования метода угловых точек для определения взаимовлияния фундаментов
Для вычисления крена необходимо определить осадки в точках М1 и М2, лежащих на контуре рассматриваемого прямоугольника, но за пределами контура загруженного прямоугольника Б. В этом случае осадка в точке М1
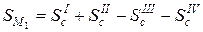
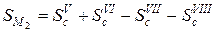
Крен фундамента f можно найти, отнеся разность осадок сторон фундамента к его ширине:
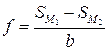
где f — тангенс угла наклона подошвы.
5.3.7. Расчет осадок фундаментов на слоистой толще грунтов
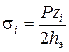
где P – внешнее давление на уровне подошвы фундамента; zi – расстояние от точки, соответствующей глубине 2hэ, до середины рассматриваемого слоя.
Если принять средневзвешенное значение коэффициента сжимаемости 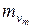
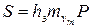
Полная осадка всей активной зоны грунта равна сумме осадок отдельных слоев:
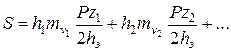
Подставив (5.39) в (5.38), получим
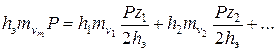
Сокращая на Р и решая относительно 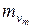
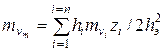
где 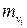
5.3.8. Расчет осадок во времени
В практике проектирования часто возникает необходимость рассчитывать осадки фундаментов во времени, так как разность осадок во времени может быть больше предельно допустимой величины (пример 13, 14). Кроме того, большое значение имеет скорость протекания осадок во времени. При медленном возрастании осадок фундаментов (даже значительных по величине) надземные конструкции зданий способны деформироваться пластически без нарушения сплошности элементов конструкций. Если же скорость осадок велика, то может произойти хрупкое разрушение отдельных элементов, что приведет к недопустимым деформациям всего здания. Поэтому расчет осадок во времени необходим при проектировании фундаментов по предельным состояниям.
В зависимости от свойств грунтов и их состояния для расчета осадок во времени принимают различные теории: теорию ползучести и теорию фильтрационной консолидации с учетом сжимаемости поровой жидкости, структурной прочности грунта при сжатии, начального градиента напора, параметров ползучести.

Разработка теории уплотнения и набухания грунтов базируется на рассмотрении дифференциального уравнения гидродинамических давлений, предложенного Н.Н.Павловским в 1922 г., в которое Н.М.Герсевановым в 1933 г. были внесены существенные поправки. Дальнейшее развитие теория получила в трудах В.А.Флорина, С.А.Роза, Д.Е.Польшина, Н.А.Цытовича, З.Г.Тер-Мартиросяна, Ю.К.Зарецкого и др. К.Терцаги (1925) принял для описания процесса консолидации уравнение по аналогии между тепловым и фильтрационным движением. В этих трудах даны уравнения гидродинамических напряжений для случая плоской и пространственной задачи в сжимаемой среде с переменной пористостью, проницаемостью, уплотняемостью, а также для грунтов, содержащих связанную воду. В двухфазных системах, содержащих в порах свободную воду (“грунтовая масса”), уплотнение грунта происходит за счет отжатия воды из пор. Это отжатие происходит тем медленнее, чем ниже водопроницаемость грунта.
Процесс уплотнения грунта во времени, вследствие уменьшения влажности (пористости) при постоянном напряженном состоянии называется процессом консолидации. Обратный процесс увеличения объема грунта вследствие повышения влажности (пористости) при постоянном напряженном состоянии в процессе разгрузки носит название процесса набухания.
При обжатии слоя грунта ограниченной мощности равномерно распределенной нагрузкой, т.е. при сжатии без возможности бокового расширения, вода может отжиматься лишь в направлении расположения водопроницаемой прослойки.
На схеме рис.5.11,а показан случай односторонней фильтрации, на схеме рис.5.11,б — двухсторонней фильтрации.
 |
Рис.5.11. Распределение напряжений в «грунтовой массе» в ходе процесса консолидации:
а – при односторонней фильтрации; б – при двухсторонней фильтрации; в – после окончания консолидации
Давления, приложенные извне, вызывают в системе, иллюстрированной моделью (с пружиной), полные напряжения Р; напряжения, которые в процессе консолидации воспринимаются водой, называются нейтральными (поровыми) напряжениями Pw, а напряжения, воспринимаемые скелетом грунта, носят название эффективных напряжений Pz. Очевидно, процесс консолидации во времени заключается в постепенном понижении нейтральных напряжений и росте эффективных. При полном восприятии нагрузки скелетом консолидация заканчивается (рис.5.11,в).
Выделим на рис.5.11,а столбик высотой h и основанием, площадь которого равна единице. В определенный момент времени t от начала консолидации распределение нейтральных и эффективных напряжений определится эпюрой I. Через некоторый промежуток времени dt это распределение изменится и будет изображаться эпюрой II. Кривые I и II представляют собой линии равных напоров, называемые изохронами. В начальный момент консолидации изохроной будет прямая ab, а в конечный – cd. Выделим в рассматриваемом столбике двумя горизонтальными сечениями слой толщиной dz. Полное напряжение в нем – Р, эффективное – Рz, нейтральное (поровое) – Рw:
Для любого промежутка времени dt в элементарном слое грунта увеличение расхода воды dq будет равно уменьшению влажности (пористоcти), т.е. можно положить:
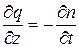
После ряда преобразований уравнение гидродинамических давлений может быть представлено для одномерной задачи в виде
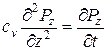
где cv – коэффициент консолидации, величина которого зависит от свойств грунта,
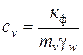
где кф – коэффициент фильтрации; mv – коэффициент относительной сжимаемости грунта; gw – удельный вес воды.
Решение дифференциального уравнения (5.43) находится путем применения ряда Фурье. При равномерном распределении уплотняющих давлений по глубине в стабилизированном состоянии (рис.5.12,а) решение уравнения (5.43) может быть представлено в виде
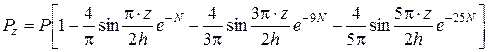
где 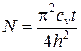
Если известно напряжение Рz в слое dz по прошествии времени t от момента загрузки, то можно вычислить деформации этого слоя:
Осадку поверхности слоя грунта толщиной h за время t найдем, взяв интеграл выражения (5.47) в пределах от 0 до h:
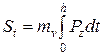
Подставив в (5.48) значение Pz из (5.45) получим после интегрирования
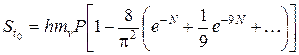
Формула (5.49) для основного случая 0 (рис.5.12,а), когда эпюра уплотняющих давлений по глубине слоя грунта имеет вид прямоугольника (пример 13). Другими важными для практики случаями будут случай 1, когда уплотняющее давление возрастает с глубиной по закону треугольника (рис. 5.12,б), и случай 2, когда уплотняющее давление убывает с глубиной по закону треугольника.
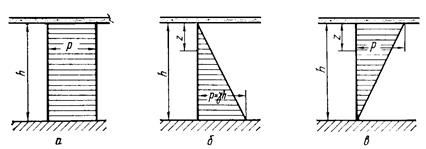 |
Случай 1 имеет место, например, при уплотнении грунта под давлением собственного веса:
Рис. 5.12. Различные случаи распределения уплотняющих давлений
по глубине для одномерной задачи
Случай 2 сводится к ранее рассмотренным случаям, т.к.
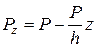
На основании решения дифференциального уравнения консолидации (5.43) с учетом (5.47), (5.50), (5.51) получены формулы для определения осадок во времени для случаев 1 и 2:
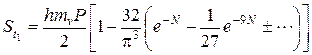
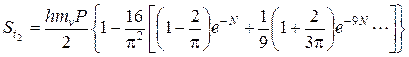
Задаваясь различными значениями времени t, можно по формуле (5.46) найти величину N и, подставляя ее в формулы (5.49), (5.52), (5.53), получить осадки во времени St. Это громоздко. Для практических расчетов введено понятие о степени консолидации, равной отношению осадки St к полной осадке S:
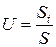
Для различных значений степени консолидации U = 0,1; 0,2; 0,3. 0,95 для расчетных схем рис.5.12 составлены таблицы значений N (табл.IV.6 приложения IV; пример 14).
Задаваясь различными значениями степени консолидации, находим N и по формуле (5.46) определяем время t, в течение которого достигается данная степень консолидации:
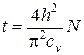
Осадки во времени при соответствующей степени консолидации
По результатам расчета строим график осадки слоя грунта во времени (рис.5.13)
Время полной консолидации с достаточной степенью точности может быть найдено из пропорциональной зависимости между временем равного уплотнения слоев разной мощности. Если при этом обозначить через h и t соответственно высоту образца грунта и время его полного уплотнения при компрессионных испытаниях, а через H – мощность того же слоя грунта под соответствующей нагрузкой от сооружения, то время полной осадки сооружения Т может быть легко определено из зависимости 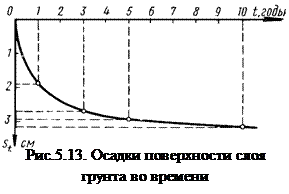
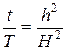
| | | следующая лекция ==> | |
| Осадка слоя грунта при сплошной нагрузке | | | Глобальные проблемы современности. Футурология и глобалистика. |
Дата добавления: 2016-05-11 ; просмотров: 3220 ;
Источник