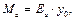Эпюра изгибающих моментов фундамента

iSopromat.ru

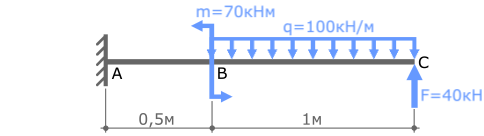
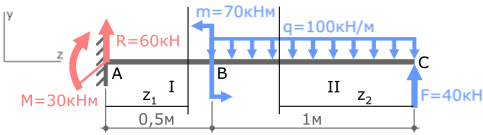
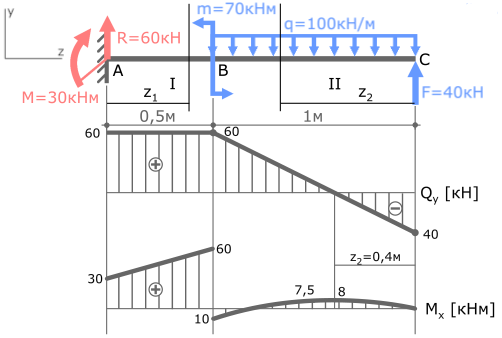
Пример решения задачи на построение эпюры внутренних изгибающих моментов M_x для стальной консольной балки нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.

Задача

Пример решения

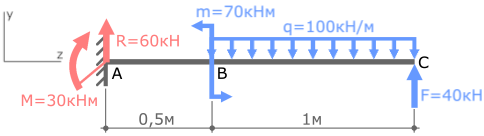
Покажем найденные опорные реакции и выбранную систему координат.

Для построения эпюры изгибающих моментов M_x запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

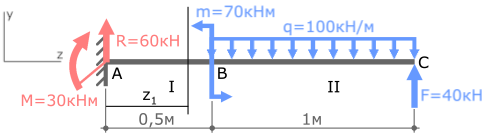
Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Q_y.

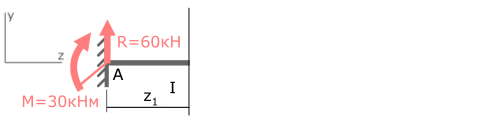
Рассмотрим I силовой участок:

Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.

Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.

Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.

По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:

В выражении переменная z₁ в первой степени, поэтому эпюра M_x на первом участке будет иметь вид прямой линии.

Рассчитаем значения M_xI на границах участка, т.е. при z₁=0 и при z₁=0,5м

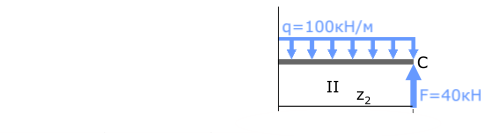
Переходим на второй силовой участок:

Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.

Получено выражение с переменной z₂ во второй степени, значит, эпюра M_x на втором участке будет иметь вид параболы.

Видео про построение эпюр:

Для построения параболы требуется как минимум три точки. Этими точками будут значения M_x на границах и в середине II силового участка, то есть при z₂=0, z₂=1м и z₂=0,5м.

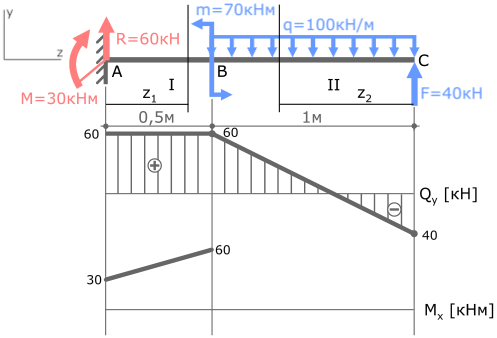
По полученным данным строим эпюру изгибающих моментов M_x (готовую эпюру Q_y перенесем из ранее рассмотренной задачи)

Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Q_y.

Q_y — первая производная от M_x. Поэтому в том месте, где Q_y пересекает базовую линию (т.е. Q_y=0) на эпюре M_x будет экстремум.

Видео про расчет экстремума эпюры:

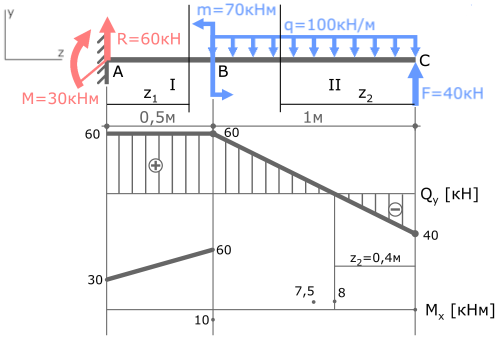
Рассчитаем значение экстремума эпюры M_x на II участке балки.

1. Выражение Q_yII приравняем к нулю
   Q_yII=100z₂-40=0
2. Выразим из него z₂
   z₂=40/100=0,4м
3. Подставим z₂ в выражение для M_{xII
   MxIIэкстр(z2=0,4м)= -50∙0,4 2 +40∙0,4=8кНм}

Отметив эту точку в области эпюры где Q_y=0 соединим ее с тремя другими параболой.

Эпюра изгибающих моментов построена. Проверка эпюры M_x.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

Эпюрами внутренних поперечных сил и изгибающих моментов называют графическое представление распределения функций Q и M по длине балки при изгибе.

Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.

Рассмотрим некоторые примеры на построение эпюр в балках:

Эпюры при чистом изгибе

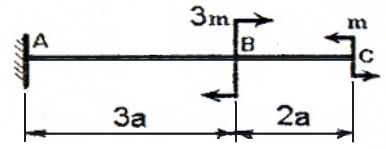
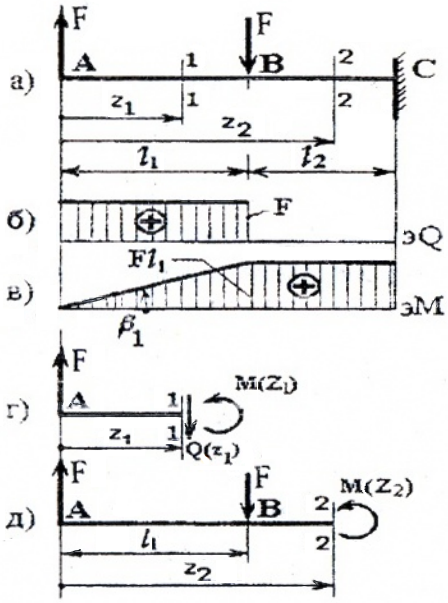
Для консольной балки:

имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.

Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
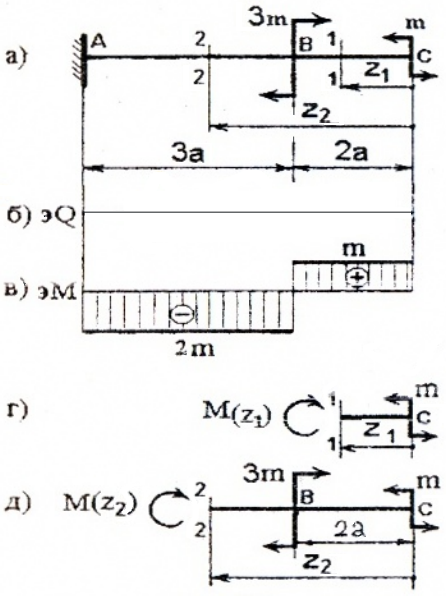
I силовой участок (BC): 0 ≥ z₁ ≥ 2a (рис. 2 а,г)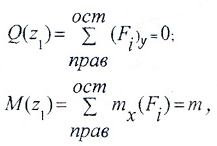

т.е. Q(z₁)=0 на всем участке, а M(z₁)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.

II силовой участок (AB): 2a ≥ z₂ ≥ 5a (рис. 2 а,д)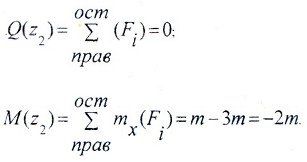

Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).

Более нагруженным оказался участок AB, он и является опасным: M_max=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.

Эпюры при поперечном изгибе

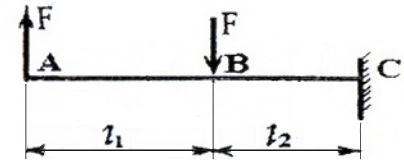
Построение эпюр Q и M для балки, изображенной на рис. 3

проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.

I силовой участок (AB): 0 ≥ z₁ ≥ l₁ (рис. 4, а, г)
Q(z₁)= F=const, на всем участке постоянная величина,
M(z₁)=F×z₁, уравнение прямой, график строим по двум граничным точкам:
M(z₁=0)=F×0=0 – в сечении A;
M(z₁=l₁)=F× l₁ — в сечении B.

Опасным является сечение B, в котором действуют Q_max=F, M_max=Fl₁.

Геометрическая проверка эпюр

Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
Для всех силовых участков находим: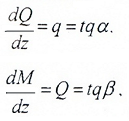

где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α₁=0 (линия эпюры Q горизонтальна), следовательно,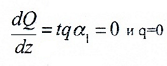

распределенная нагрузка отсутствует;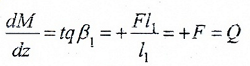

функция M (z₁) – возрастающая.

На участке “BC”: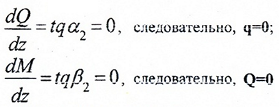

Так как все дифференциальные проверки выполняются, эпюры построены верно.

Эпюры для двухопорных балок

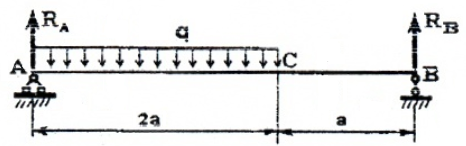
Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),

необходимо вначале найти опорные реакции и только потом строить эпюры.

Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑M_A=0 и ∑M_B=0.

Записываем уравнения и находим значения реакций: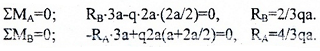

Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑F_Y=0 или ∑M_С=0.

Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).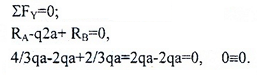

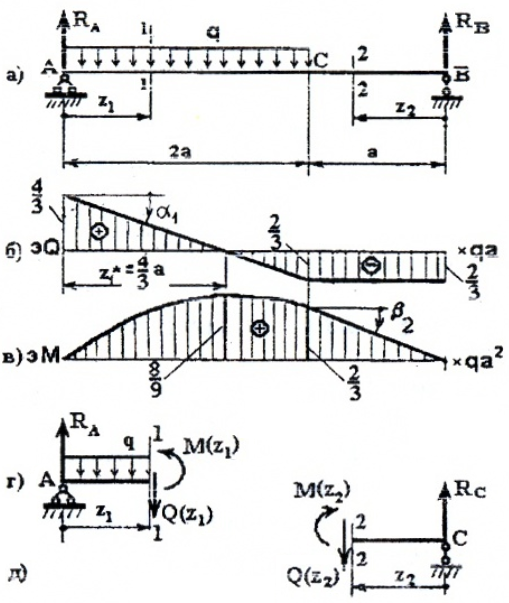
Для построения эпюр рассмотрим два силовых участка:

I участок (AC): 0 ≥ z₁ ≥2a (рис. 6, а, г)
Q(z₁)=R_A-qz₁ — прямая, которую строим по двум граничным точкам: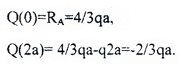

M(z₁)=R_Az₁-qz₁(z₁/2)= R_Az₁-qz₁ 2 /2 – парабола.

Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует M_max(z*), и дифференциальной зависимости: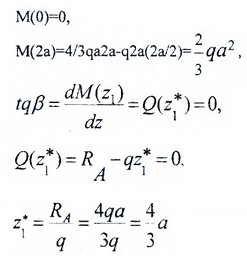

Определяем экстремум эпюры M на участке: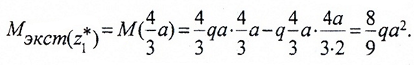

II участок (BC): 0 ≥ z₂ ≥ a (рис. 6, а, д)
Q(z₂)= -R_B= -2/3qa;
M(z₂)=R_Bz₂,
M(z₂=0)=0,
M(z₂=a)=2/3qa 2 .
Выполним проверку дифференциальных зависимостей.
I силовой участок: 0 ≥ z₁ ≥ 2a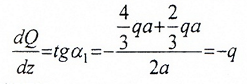

— направлена вниз, функция Q(z₁) – убывающая.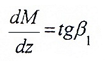

— проверка визуально: чем больше угол наклона β₁, тем больше значение Q(z₁).

II силовой участок: 0 ≥ z₂ ≥ a.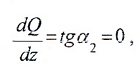

следовательно, q=0.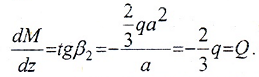

функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z₁*=4/3a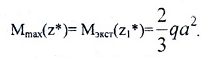

По силе в сечении «A»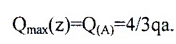

После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Расчётные схемы внецентренно нагруженных ленточных фундаментов под несущие стены. Расчёт и конструирование ленточных фундаментов под ряды колонн. Метод прямолинейной эпюры

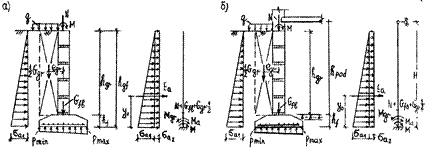
Существуют две основные расчётные схемы внецентренно нагруженных ленточных фундаментов под несущие стены в зависимости от очерёдности устройства пола подвала, надподвального перекрытия и производства обратной засыпки грунта.

Схема 1.Обратная засыпка грунта за пазухи фундамента производится до устройства пола подвала и надподвального перекрытия. Расчётная схема фундамента принимается в этом случае в виде консольного стержня с жёстким защемлением в уровне его подошвы (рис. 19, а). В результате изгибающий момент от активного давления грунта может быть вычислен по формулам:

,

.

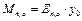
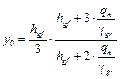
Схема 2. Обратная засыпка грунта за пазухи фундамента производится после устройства пола подвала и надподвального перекрытия. Расчётная схема фундамента в этом случае принимается в виде вертикального стержня с шарнирно неподвижной опорой в уровне перекрытия над подвалом и жёстким защемлением в уровне подошвы фундамента (рис. 19, б). Изгибающий момент от активного давления грунта вычисляют по следующим зависимостям:

,

,

, ,

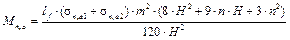
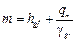
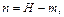
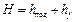
h_f — высота блок-подушки (монолитной ленты).

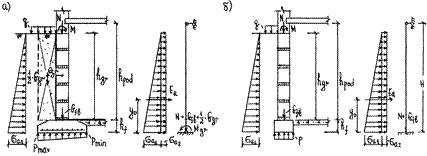
При устройстве мягкой гидроизоляции поверху блок-подушки (рис. 20, а) в расчётной схеме фундамента принимают шарнирное закрепление в нижней части стены подвала (схема 3), согласно которому изгибающие моменты от внешней нагрузки и от активного давления грунта в этом уровне равны нулю:

, .

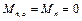
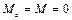
Рис. 19. Расчётные схемы внецентренно нагруженного ленточного фундамента при производстве обратной засыпки грунта: а – до устройства пола подвала и надподвального перекрытия, б – после устройства пола подвала и надподвального перекрытия

Приведенные три схемы справедливы для монолитных и сборных железобетонных фундаментов при отношении ширины фундаментных блоков к ширине блок-подушки b_fb / b_f ≤ 0,7 и ширине блок-подушки b_f ≥ 1 м. При невыполнении этих условий для сборных ленточных фундаментов используют схему 4 (рис. 20, б), которая идентична схеме 3, но фундамент считают центрально нагруженным:

, .

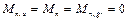
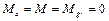
Рис. 20. Расчётные схемы внецентренно нагруженного ленточного фундамента: а – при устройстве мягкой гидроизоляции поверху блок- подушки, б – для сборных фундаментов при b_fb / b_f > 0,7 и b_f

,

, .

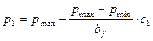
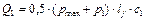
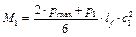
Также аналогичен расчёт блок-подушки в сечении 1-1 по образованию и раскрытию трещин.При этом изгибающий момент М_n,1 и отпор грунта (p_n,max , p_n,min , p_n,1) вычисляют от нормативных нагрузок. Первоначально проверяют условие

.

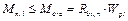
Если оно не соблюдается, то расчёт ширины раскрытия трещин a_crc,2 и a_crc,1 выполняют по аналогии с проверками плитной части отдельных фундаментов под колонны.

Ленточные железобетонные фундаменты под ряды колонн выполняют с тавровым поперечным сечением и преимущественно монолитными (рис. 21, поз. 1). Ширину подошвы b_f (рис. 21, поз. 6) ленточного фундамента обычно принимают постоянной по длине. В том случае, если имеются участки с резко повышенной нагрузкой, устраивают местное уширение подошвы фундамента. Толщину полки у наружного края принимают не менее 200 мм (рис. 21, б), а толщину полки у ребра h_pl (рис. 21, поз. 9) из расчёта, чтобы поперечная сила от отпора грунта могла быть воспринята только бетоном без поперечного армирования ленты.

Рис. 21. Конструктивные элементы ленточного фундамента под ряды колонн: а – продольный разрез, б – опирание монолитной колонны, в – опирание сборной колонны

При консольных вылетах плитной части не более 75 см её толщину (рис. 21, поз. 12) рекомендовано принимать постоянной, а при больших вылетах — переменной с утолщением к ребру, но с уклоном i ≤ 1:3 (рис. 21, поз. 13). Ширину ребра b_r (рис. 21, поз. 10) принимают исходя из размеров опирающихся на него колонн. При монолитных колоннах (рис. 21, б) ширина ребра должна быть шире колонны не менее чем на 50 мм в каждую сторону от её грани для удобства установки опалубки колонны. При сборных колоннах (рис. 21, в, поз. 4) ширину ребра принимают равной ширине подколонника (рис. 21, поз. 3). Высоту ребра h_r (рис. 21, поз. 8) принимают постоянной по всей длине фундаментной ленты l_f (рис. 21, поз. 7). Она зависит от глубины заложения фундамента и уровня его обреза.

Характер напластования грунтов (их податливость) определяет выбор метода расчёта ленточного фундамента, а его геометрические характеристики и, прежде всего, высота ребра h_r — категорию жёсткости. Ленточные фундаменты под колонны разделяют на две основные категории:

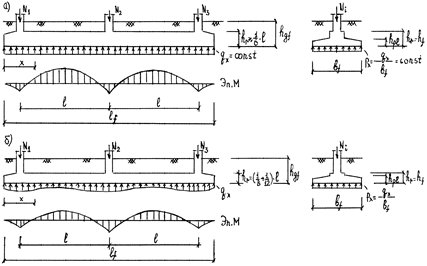
1. Условно абсолютно жёсткиефундаменты, которые в силу своих конструктивных особенностей (h_r ≥ 1/6∙l , где l — шаг колонн) практически не изгибаются в продольном направлении под действием внешних нагрузок. Реактивное давление грунта по подошве таких фундаментов определяют без учёта их совместной работы с основанием (деформации фундаментов малы по сравнению с деформациями основания). Принимается, что реактивное давление грунта изменяется по линейному закону не только по ширине фундаментной ленты, но и по её длине (рис. 22, а).

Рис. 22. Эпюры реактивного давления грунта и изгибающих моментов в ленточных фундаментах под ряды колонн: а – условно абсолютно жёсткий фундамент, б – гибкий фундамент

2. Гибкиефундаменты, которые в силу своих конструктивных особенностей (h_r 3 , а при наличии подвала — γ_m = 17 кН/м 3 );

— сумма продольных сил от нормативных вертикальных нагрузок на все колонны ленточного фундамента.

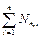
При монолитных ленточных фундаментах величину b_f принимают в большую сторону кратно 100 мм, а при сборных подбирают блок-подушку большего размера по каталогу. После этого уточняют значение расчётного сопротивления грунта основания R.

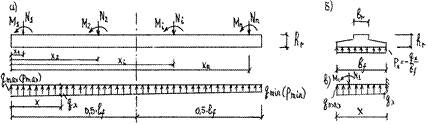
Для жёстких ленточных фундаментов дальнейшие расчёты выполняют по методу прямолинейной эпюры. Для гибких ленточных фундаментов этот метод используют как предварительный с целью подбора размеров поперечного сечения фундаментной ленты. Согласно этому методу реактивное давление принимают по прямолинейной эпюре, которое при симметричном нагружении ленты вдоль её оси имеет вид прямоугольника, а при несимметричном нагружении – вид трапеции (рис. 23, а). Первоначально проверяют краевые давления на грунт от нормативных нагрузок с учётом собственного веса фундамента и грунта на его уступах:

,

,

— момент сопротивления подошвы фундамента;

— сумма всех нормативных вертикальных нагрузок на фундаментную ленту;

— сумма моментов от всех нормативных вертикальных нагрузок на фундаментную ленту (за положительный принимают момент против хода часовой стрелки);

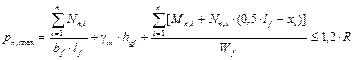
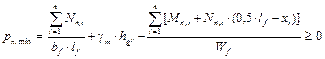
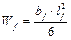
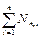
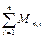
x_i — расстояние от левого конца фундаментной ленты до оси i-ой колонны.

При выполнении указанных условий производят расчёт основания по второй и первой группе предельных состояний, а затем переходят к расчётам фундаментной ленты по несущей способности. В этом случае реактивное давление грунта определяют от расчётных нагрузок без учёта собственного веса фундамента и грунта на его уступах по формулам:

Рис. 23. Расчётные схемы ленточного фундамента под ряды колонн по методу прямолинейной эпюры: а – вдоль оси ленты, б – в поперечном направлении, в – при определении внутренних усилий

,

,

.

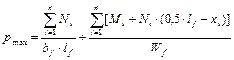
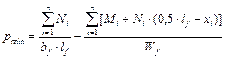
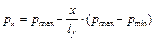
Изгибающие моменты и поперечные силы в фундаментной ленте вычисляют как в консольной балке, вводя условную заделку в заданном сечении x (рис. 23, в):

,

,

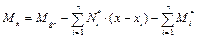
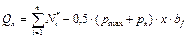
M_gr — изгибающий момент в заданном сечении от реактивного давления (отпора) грунта,

;

— сумма изгибающих моментов от вертикальных нагрузок, расположенных левее заданного сечения;

— сумма изгибающих моментов, передаваемых колоннами, расположенными левее заданного сечения.

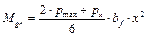
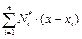
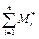
По величине найденного максимального изгибающего момента М_x,max определяют необходимый по условию прочности (как для бетонного фундамента) момент сопротивления поперечного сечения W, а по нему уточняют ранее принятые конструктивные размеры фундаментной ленты и вычисляют её его изгибную жёсткость EJ:

, , ,

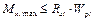
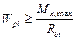
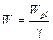
R_bt — расчётное сопротивление бетона фундаментной ленты растяжению;

W_pl , W — соответственно упругопластический и упругий моменты сопротивления поперечного сечения фундаментной ленты;

γ — коэффициент, учитывающий форму поперечного сечения (γ = 1,2 для таврового сечения с полкой в нижней зоне).

Источник