Определение напряжений по подошве фундаментов и сооружений
Общие положения. При взаимодействии фундаментов и сооружений с грунтами основания на поверхности контакта возникают контактные напряжения. Знание контактных напряжений необходимо как для расчета напряжений в основании, создаваемых сооружением, так и для расчетов самих конструкций.
Отметим, что расчет сооружений на действие контактных напряжений обычно рассматривается в курсе строительной механики.
Характер распределения контактных напряжений зависит от жесткости, формы и размеров фундамента или сооружения и от жесткости (податливости) грунтов основания. Различают три случая, отражающих способности сооружения и основания к совместной деформации:
1) абсолютно жесткие сооружения, когда деформируемость сооружения ничтожно мала по сравнению с деформируемостью основания, и при определении контактных напряжений сооружение можно рассматривать как недеформируемое;
2) абсолютно гибкие сооружения, когда деформируемость сооружения настолько велика, что оно свободно следует за деформациями основания;
3) сооружения конечной жесткости, когда деформируемость сооружения соизмерима с деформируемостью основания; в этом случае они деформируются совместно, что вызывает перераспределение контактных напряжений.
Характерными примерами абсолютно жестких конструкций являются массивные фундаменты под мостовые опоры, дымовые трубы, тяжелые прессы, кузнечные молоты и т. д., абсолютно гибких – земляные насыпи, днища металлических резервуаров и т. п. Большинство сооружений (плитные фундаменты, балки, ленточные фундаменты) по условиям работы конструкций имеют конечную жесткость.
Критерием оценки жесткости сооружения может служить показатель гибкости по М.И. Горбунову-Посадову
е ≈ 10 (El 3 /Eкh 3 ), (8.1)
где Е и Ек — модули деформации грунта основания и материала конструкции; l и h — длина и толщина конструкции.
Конструкция сооружения или фундамента считается абсолютно жесткой, если t≤1. В первом приближении жесткость конструкции можно оценить исходя из соотношения ее толщины и длины. При h/l>1/3 конструкция может рассматриваться как абсолютно жесткая.
Существенное значение имеет также соотношение длины l и ширины b сооружения. При 1/b≥0 распределение контактных напряжений соответствует случаю плоской задачи, при. l/b 2 ) – цилиндрическая жесткость полосы; f(x) –интенсивность заданной на полосу нагрузки; р(х) – интенсивность неизвестной эпюры контактных напряжений. Напомним, что индекс «к» относится к конструкции; следовательно, Ек и vк – соответственно модуль упругости и коэффициент Пуассона материала полосы; Iк – момент инерции ее поперечного сечения.
В уравнении (8.2) содержатся две неизвестные величины: w(x) и р(х). Следовательно, для решения задачи необходимо введение дополнительного условия. Это условие определяется в зависимости от принятия той или иной модели: местных упругих деформаций или упругого полупространства.
Модель местных упругих деформаций.Предпосылки этой модели впервые были сформулированы русским академиком Фуссом в 1801 г., а сама модель разработана в 1867 г. Винклером для расчетов железнодорожных шпал. В дальнейшем модель местных упругих деформаций была развита в работах Н. П. Пузыревского, С. П. Тимошенко, А. Н. Крылова, П. Л. Пастернака и др.
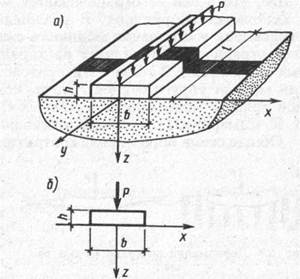
Рис. 8.2. Схема балки (а) и расчетная схема для случая плоской задачи (б)
Согласно этой модели, реактивное напряжение в каждой точке поверхности контакта прямо пропорционально осадке поверхности основания в той же точке:
p(x) = kw(x), (8.3)
где к — коэффициент пропорциональности, часто называемый коэффициентом постели, Па/м.
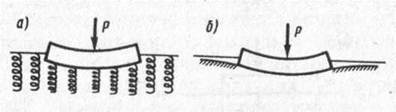
Схема деформирования такого основания показана на рис. 8.3, а. Видно, что в соответствии с моделью местных упругих деформаций осадки поверхности основания за пределами габаритов фундамента отсутствуют, т. е. фундамент как бы установлен на пружинах, сжимающихся только в пределах его контура.
Рис. 8.3. Деформации поверхности основания: а – по модели упругих деформаций; б – по модели упругого полупространства
Модель упругого полупространства. Эта модель была предложена Г. Э. Проктором в 20-х годах нашего столетия и развита благодаря работам Н. М. Герсеванова, М. И. Горбунова-Посадова, Б. Н. Жемочкина, А. П. Синицына и других ученых.
В отличие от предыдущей модели в этом случае поверхность грунта оседает как в пределах площади загрузки, так и за ее пределами (рис. 8.3, б), причем кривизна прогиба зависит от механических свойств грунтов и мощности сжимаемой толщи в основании.
В случае плоской деформации прогиб поверхности под действием сосредоточенной силы Р описывается уравнением
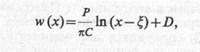
где С = Е/(1 – ν 2 ) – коэффициент жесткости основания; х — координата точки поверхности, в которой определяется осадка; ζ — координата точки приложения силы Р; D — постоянная интегрирования. При определении прогибов поверхности от действия распределенной нагрузки уравнение (8.4) следует проинтегрировать по площади загружения.

Недостаток модели упругого полупространства заключается в том, что в ней не ограничивается мощность сжимаемой толщи в основании сооружения. В реальных условиях взаимодействия фундамента и основания мощность сжимаемой толщи обычно бывает ограничена, что влияет на характер распределения контактных напряжений. В связи с этим разработаны различные модификации модели упругого слоя грунта, подстилаемого недеформируемой толщей, приведенные в работах О. Я. Шехтер, К. Е. Егорова, И. К. Самарина, Г. В. Крашенинниковой и др.
Общая схема определения контактных напряжений с использованием указанных выше моделей заключается в совместном решении уравнения (8.2) и условия (8.3) в случае модели местных упругих деформаций или уравнений (8.2) и условия типа (8.4) в случае модели упругого полупространства. Методы решения этих задач приведены, например, в учебнике П. Л. Иванова (1991).
Для практических расчетов контактных напряжений используются приведенные в табличной форме решения М. И. Горбунова-Посадова, Б. Н. Жемочкина, А. П. Синицьша, Г. В. Крашенинниковой и др. Наиболее полные сведения по этому вопросу представлены в монографии М. И. Горбунова-Посадова, Т. А. Маликовой, В. И. Соломина «Расчет конструкций на упругом основании», удостоенной в 1987 г. Государственной премии СССР.
Область применения различных моделей. Практика расчетов показывает, что модель местных упругих деформаций позволяет получить хорошее совпадение с действительностью при возведении фундаментов на сильносжимаемых грунтах (при Е≤ 5 МПа), на лёссовых просадочных грунтах, а также при ограниченной толще сжимаемых грунтов, подстилаемых практически недеформируемыми, например скальными породами. Модель упругого полупространства применима при наличии в основании достаточно плотных грунтов и при не слишком больших площадях опорных поверхностей. Для сооружений с площадью опирания в десятки и сотни квадратных метров более близкие к действительности результаты дает модель упругого слоя ограниченной мощности.
Контактные напряжения на подошве центрально-загруженных абсолютно жестких фундаментов.При определении контактных напряжений в этом случае исходят из того, что вертикальные перемещения любой точки поверхности грунта в уровне подошвы одинаковы, т. е. w(x,у)=const. Тогда для круглого в плане фундамента контактные напряжения определятся выражением
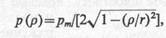
где рm — среднее напряжение под подошвой фундамента радиусом r; ρ — расстояние от центра фундамента до точки, в которой определяется ордината контактного напряжения р(ρ).
Аналогичным образом определяются и контактные напряжения под жестким полосовым фундаментом в случае плоской задачи:
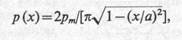
где х — расстояние от середины фундамента до рассматриваемой точки; а = b/2— полуширина фундамента.
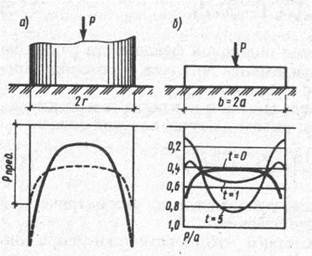
Приведенные решения показывают, что теоретически эпюра контактных напряжений под жестким фундаментом имеет седлообразный вид с бесконечно большими значениями напряжений по краям (при ρ = r или x=b/2). Однако вследствие пластических деформаций грунта в действительности контактные напряжения характеризуются более пологой кривой и у края фундамента достигают значений, соответствующих предельной несущей способности грунта (пунктирная кривая на рис. 8.4, а).
Рис. 8.4. Эпюры контактных напряжений: a — под жестким круглым штампом; б— под плоским фундаментом при различном показателе гибкости
Изменение показателя гибкости существенно сказывается на изменении характера эпюры контактных напряжений. На рис. 8.4, б в качестве примера приведены контактные эпюры для случая плоской задачи при изменении показателя гибкости t от 0 (абсолютно жесткий фундамент) до 5.
Как отмечалось выше, достоверное знание контактных напряжений необходимо для расчетов конструкции фундаментов сооружений, взаимодействующих с грунтом. При расчетах напряжений в основаниях от действия нагрузок, соответствующих контактным напряжениям, часто оказывается возможным вводить существенные упрощения. Это связано с тем, что неравномерное распределение контактных напряжений по подошве фундамента оказывает заметное влияние на изменение напряжений лить в верхней части основания на глубину порядка половины ширины фундамента.
Упрощенное определение контактных напряжений. Если контактные напряжения по подошве фундамента определяются для последующих расчетов напряжений в основании, то допускается независимо от жесткости фундамента .использовать формулы внецентренного сжатия. Тогда для центрально-нагруженного силой Р фундамента будет иметь место равномерное распределение напряжений по его подошве: р=Р/А, где А — площадь фундамента. В случае плоской задачи при нагружении фундамента силой Р и моментом М, действующим в этой плоскости, краевые значения контактных напряжений определятся выражением
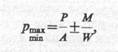
где W — момент сопротивления площади подошвы выделенной полосы фундамента. Распределение контактных напряжений между этими значениями будет иметь линейный характер.
Теперь уже распределение напряжений в основании ниже подошвы фундамента можно рассчитать, если рассматривать полученную таким образом эпюру контактных напряжений как абсолютно гибкую местную нагрузку, действующую в этой плоскости.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Как распределяется напряжение в основании. Определение несущей способности основания
Чтобы рассчитать осадку фундамента и проверить прочность (несущую способность) основания, нужно знать распределение напряжений в основании, т. е. его напряженное состояние. Необходимо иметь сведения о распределении напряжений не только по подошве фундамента, но и ниже нее, так как осадка фундамента является следствием деформации толщи грунта, расположенной под ним. Для расчета несущей способности основания также приходится определять напряжения в грунте ниже подошвы фундамента. Без этого нельзя установить наличие и размеры областей сдвигов, проверить прочность прослойки слабого грунта и т. д.
Для теоретического определения напряжений в основании используют, как правило, решения теории упругости, полученные для линейно деформируемого однородного тела. В действительности грунт не является ни линейно деформируемым, телом, так как деформации его не прямо пропорциональны давлению, ни однородным телом, так как плотность его меняется с глубиной. Однако эти два обстоятельства не сказываются существенно на распределении напряжений в основании.
В данной главе рассматриваются не все вопросы напряженного состояния оснований, а только методика определения нормальных напряжений, действующих в грунте по горизонтальным площадкам.
Распределение напряжений по подошве фундамента
В мостовом и гидротехническом строительстве, как правило, применяют жесткие фундаменты, деформациями которых можно пренебречь, поскольку они малы по сравнению с перемещениями, связанными с осадкой.
Измерения нормальных напряжений (давлений) по подошве фундамента, выполненные с помощью специальных приборов, вмонтированных на уровне подошвы, показали, что эти напряжения распределены по криволинейному закону, зависящему от формы и размеров фундамента в плане, свойств грунта, среднего давления на основание и других факторов.
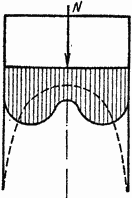
В качестве примера на рис. 2.1 сплошной линией показано фактическое распределение нормальных напряжений (эпюра нормальных напряжений) по подошве фундамента, когда нагрузка (сила N) значительно меньше несущей способности основания, а пунктиром — распределение напряжений, полученное на основе решений теории упругости.
В настоящее время, несмотря на накопленный экспериментальный материал и теоретические исследования, не представляется возможным устанавливать в каждом конкретном случае действительное распределение давлений по подошве фундамента. В связи с этим в практических расчетах исходят из прямолинейных эпюр давлений.
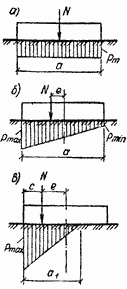
Рис. 2.2. Прямолинейные эпюры нормальных напряжений по подошве фундамента а — при центральном сжатии; б— при внецентренном сжатии и e W/AПри центральном сжатии (рис. 2.2, а) напряжения Pm, кПа, по подошве принимают равномерно распределенными и равными:
Pm = N/A, (2.1)
где N — нормальная сила в сечении по подошве фундамента, кН; А — площадь подошвы фундамента, м 2 .
При внецентренном сжатии эпюру напряжений принимают в виде трапеции (рис. 2.2, б) или треугольника (рис. 2.2, в). В первом из этих случаев наибольшее ртах и наименьшее Pmin напряжения определяются выражениями:
Pmax = N/A + M/W;
Pmin = N/A – M/W (2.2)
где M — Ne — изгибающий момент в сечении по подошве фундамента, кН·м (здесь е — эксцентриситет приложения силы N, м); W — момент сопротивления площади подошвы фундамента, м 3 .
Формулы (2.2) справедливы в случаях, когда изгибающий момент действует в вертикальной плоскости, проходящей через главную центральную ось инерции подошвы фундамента.
При подошве фундамента в виде прямоугольника с размером, перпендикулярным плоскости действия момента М, b и другим размером a имеем A = ab и W = ba2/6. Подставляя выражения A и W в формулы (2.2) и учитывая, что M = Ne, получаем:
Pmax =N/ba(1+6e/a)
Pmin=N/ba(1-6e/a) (2.3)
Напряжение Pmin, кПа, вычисленное по формуле (2.2) или (2.3) при эксцентриситете e> W/A, получается отрицательным (растягивающим). Между тем в сечении по подошве фундамента таких напряжений практически быть не может. При е> W/A край подошвы фундамента, более удаленный от силы N, поднимается под действием этой силы над грунтом. На некотором участке подошвы фундамента (со стороны этого края) контакт между фундаментом и грунтом нарушается (происходит так называемое отлипание фундамента от грунта), а потому эпюра напряжений P имеет вид треугольника (см. рис. 2.2, в). Этого обстоятельства формулы (2.2) и (2.3) не учитывают, поэтому ими нельзя пользоваться при е> W/A.
Формулы для определения размера а1, м, части подошвы, по которой сохраняется контакт фундамента с грунтом, и наибольшего напряжения Pmax, кПа (см. рис. 2.2, в), можно получить, если учесть, что напряжения P должны уравновесить силу N, кН, действующую на расстоянии с от ближайшего к этой силе края подошвы фундамента.
Отсюда вытекают два условия: 1) центр тяжести эпюры напряжений P расположен на линии действия силы N; 2) объем эпюры равен величине этой силы. Из первого условия при прямоугольной подошве фундамента следует
А1=3с, (2.4)
а из второго
(Pmax а1/2)b = N. (2.5)
Из формул (2.4) и (2.5) получаем
Pmax =2N/(3cb). (2.6)
Итак, при эксцентриситете е> W/A = a/6 наибольшее давление по прямоугольной подошве фундамента Pmax следует определять по формуле (2.6).
Источник