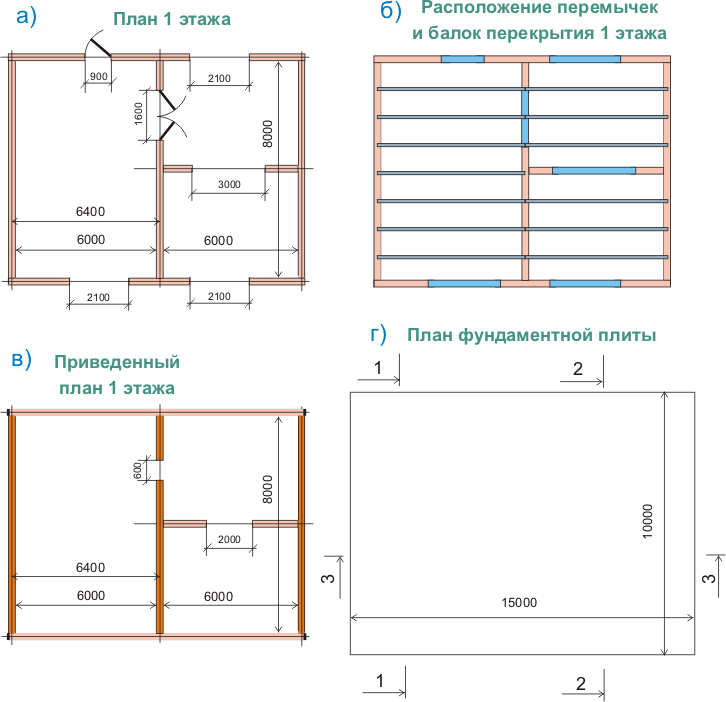
Армирование ленточного фундамента
Ленточные монолитные фундаменты обычно делаются под сплошные стены и в этом случае армирование фундамента по расчету вроде бы и не требуется.
Лента такого фундамента с точки зрения строительной механики представляет собой балку на упругом основании — грунте, и к этой балке приложена равномерно распределенная нагрузка — сплошные стены. А потому такая балка рассматривается как абсолютно жесткая и в дополнительном усилении арматурой не нуждается.
К тому же строили как-то наши предки дома без арматуры, а иногда и вообще без фундамента и ничего, некоторые из этих построек стоят и до сих пор.
Однако все не так просто, как может показаться на первый взгляд, по ряду причин:
1. Грунт под фундаментом можно рассматривать как упругое основание с постоянными физическими свойствами далеко не всегда. Более точный ответ на вопрос, как изменяются свойства грунта под фундаментом, может дать только геологоразведка. Но в любом случае, чем больше размеры строения в плане, тем больше вероятность, что свойства грунта под ленточным фундаментом будут не одинаковыми.
2. Со временем физические свойства грунта могут изменяться в результате жизнедеятельности человека или по природным причинам (например при изменении уровня грунтовых вод). Это может приводить к неравномерной осадке основания.
Для стен из натурального или искусственного камня наиболее неблагоприятной будет ситуация, когда наибольшая осадка произойдет под одним или несколькими углами здания. В этом случае в сечениях стены появятся дополнительные растягивающие напряжения, что может привести к образованию трещин. Впрочем и дополнительные сжимающие напряжения при просадке грунта ближе к середине ленты также могут оказаться не желательными.
3. Мелкозаглубленные ленточные фундаменты могут испытывать дополнительные нагрузки из-за пучения замерзшего грунта.
4. Принимаемая при расчетах нагрузка на фундамент далеко не всегда является равномерно распределенной по всей длине ленты фундамента. Наличие окон и дверей приводит как минимум к изменению значений нагрузки, а под достаточно широкими дверями нагрузки на ленту фундамента может вообще не быть. Кроме того, нагрузка на фундамент в летнее и зимнее время может быть разной.
5. В углах сопряжения перпендикулярных лент фундамента возможны скачки напряжений, если ширина лент фундамента определена неправильно или эти ленты делаются одной ширины из технологических соображений.
Как видим, причин для армирования ленточного фундамента вполне достаточно, даже если армирование по расчету не требуется. Такое армирование называется конструктивным, т.е. принимаемым без расчета. При этом конечно же должны соблюдаться общие требования по армированию балок, а также по анкеровке арматуры. Если же ленточный фундамент делается ступенчатым, то расчет армирования подошвы фундамента — отдельная тема.
Как правило в малоэтажном строительстве различные авторы многочисленных сайтов рекомендуют использовать для продольного армирования стержни диаметром 10-12 мм, но не более 40 мм.
На чем основана данная рекомендация, я не знаю. В известной мне технической литературе подобных рекомендаций нет. Впрочем эта литература предназначена для специалистов, а не для любителей. От себя могу добавить, что при выборе диаметра арматуры для конструктивного армирования кроме вышеизложенного следует руководствоваться следующими параметрами:
1. Длина ленты — чем больше длина, тем больший диаметр арматуры следует принимать).
2. Высота и ширина ленты — чем больше высота и ширина, тем меньший диаметр арматуры можно принимать.
3. Расчетные нагрузки — тут все просто, чем меньше нагрузки тем меньший диаметр арматуры можно принимать.
Тем не менее, чтобы все вышесказанное было более наглядно, представим себе следующую ситуацию: планируется ленточный фундамент (вместо фундаментной плиты), длина ленты по одной из наружных стен 8 м, высота 1 м и ширина 0.5 м, ширина подошвы фундамента 0.8 м высота подошвы 0.2 м.
Если под одной из наружных стен, например А3 (крайняя левая стена на рисунке 345.1.в) грунт в правом верхнем углу просядет сильнее, чем посредине, то в этом случае ленту фундамента под этой стеной можно рассматривать, как консольную балку длиной 4 м, соответственно потребуется армирование в верхней части ленты фундамента.
Рисунок 345.1. Примерный план 1 этажа для расчета фундаментной плиты.
Как мы уже выяснили, равномерно распределенная нагрузка на эту стену, составляет q = 6976 ≈ 7000 кг/м. Но это была нагрузка, равномерно распределенная как по фундаменту, так и по основанию, а при просадке основания нагрузка, действующая на консольную балку, будет описываться уравнением прогиба.
Чтобы упростить задачу, предположим, что эта дополнительная нагрузка описывается уравнением квадратной параболы, т.е. изменяется от максимума на конце до нуля на опоре. Тогда изгибающий момент на опоре составит:
М = (ql/3)3l/4 = ql 2 /4 = 7000·4 2 /4 = 28000 кгс·м или 2800000 кгс·см
Примечание: в данном случае мы определили значение момента графоаналитическим методом, т.е. умножили площадь эпюры нагрузки на расстояние от центра тяжести эпюры до рассматриваемой точки — опоры балки.
Так как в данном случае лента фундамента представляет собой тавровую балку из-за наличия подошвы, то сначала нужно определить, где находится граница сжатой зоны:
M = 2800000 2 0Rb = 2800000/(80·97 2 ·117) = 0.0318
Примечание: если для упрощения расчетов данную балку рассматривать как прямоугольную шириной 0.5 м, то требуемая площадь сечения составит 8.23 см 2 , т.е. не намного больше.
Т.е. для армирования верхней зоны сечения ленты фундамента под рассматриваемой стеной в этом случае понадобится не менее 3 стержней Ø 20 мм, площадь сечения составит 9.41см 2 . Такие дела.
Примечание: если арматурные стержни будут и в нижней части сечения, т.е. в сжатой зоне, то их тоже можно учесть в расчетах. Впрочем это увеличит несущую способность балки на 3-5%, а у нас итак принята арматура с хорошим запасом.
Определение прогиба при такой нагрузке — отдельная сложная тема, но опять упростим задачу и предположим, что прогиб будет такой же (хотя в действительности прогиб будет немного меньше), как при равномерно изменяющейся нагрузке и составит (согласно расчетной схеме 2.6, таблицы 2):
f = 0.86·11ql 4 /120EI
где 0.86 — коэффициент учитывающий изменение высоты сжатой зоны сечения, который тоже требует более точного определения.
Начальный модуль упругости для бетона класса В20 составляет Е = 275000 кг/см 2 . Для определения момента инерции приведенного сечения следует решить кубическое уравнение, которое здесь не привожу. Скажу лишь, что граница сжатой области бетона будет проходить в ребре балки и потому момент инерции приведенного сечения будет составлять примерно I = 750000 см 4 .
При таких исходных данных максимальный прогиб составит:
f = 0.86·11·70·400 4 /(120·275000·750000) = 0.685 см
Это означает, что если осадка основания под этим углом будет даже незначительно больше, чем под серединой фундамента, то уже включится в работу арматура. А если разница достигнет 7 мм и больше, то арматура будет работать на полную мощность. Кроме того в материале стены появятся дополнительные растягивающие напряжения, для восприятия этих напряжений в стенах их натурального и искусственного камня обычно делается арматурный пояс по периметру.
А кроме того, наличие арматуры в фундаменте позволит соблюсти требования нормативных документов, в частности СНиП 2.02.01-83* «Основания зданий и сооружений», согласно которому относительная разность осадок по отношению к длине не должна превышать 0.002 для многоэтажных бескаркасных зданий с несущими стенами из крупных блоков или кирпича (согласно таблице 391.2).
В нашем случае Δs/L = 0.7/400 = 0.00175 2 /4 = 3600·6 2 /4 = 32400 кгс·м или 3240000 кгс·см
Это в 1.16 раза больше, чем возможный изгибающий момент в примыкающей более нагруженной ленте. Если учесть, что мы приняли сечение арматуры с хорошим запасом (в 1.154 раза), и наличие арматуры в сжатой зоне, то этого должно хватить даже не смотря на то, что в данном случае у нас не тавровая, а обычная прямоугольная балка.
К тому же возможный прогиб такой балки при неравномерной осадке фундамента будет больше, а значит у балки появится дополнительная опора — лента фундамента примыкающей стены. Все это может немного увеличить нагрузку на ленту, рассмотренную нами ранее и уменьшить нагрузку на примыкающую ленту.
Ну а насколько подобная ситуация может быть вероятна — решать вам. Я же трещины на кирпичных стенах примерно посредине (часто в районе оконного проема) наблюдал неоднократно.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630
- Расчет конструкций . Фундамент
Высота ленты 1м считается от верха подошвы до верха ленты или от низа подошвы до верха ленты?
От низа подошвы до верха ленты.
Ответьте пожалуйста, правильно ли я понял что в формуле М=ql?/4, l-это половина длинны стены и знаменатель 4 это тоже половина длины стены, и в случае со стеной 9м формула будет выглядеть так: М=7000*4,5?/4,5
И ещё, правильно ли я понял, что в формуле
M =2800000
Не совсем так. В данном случае знаменатель берется из формулы, описывающей квадратную параболу, т.е. вне зависимости от длины составляет 4. Соответственно в вашем случае М=7000*4,5?/4.
b’f — это ширина подошвы — да,
h’f — это толщина подошвы — да,
ho — это расстояние от верха ленты до верха арматуры? — нет, это расстояние от шиза подошвы до центра тяжести арматуры, расположенной в верхней области сечения ленты фундамента, так как мы рассматривали условную консольную балку и рассчитывали арматуру в верхней области сечения, а не в нижней.
Ясно всё. Спасибо большое за ответы!
Насчёт арматуры в нижней зоне. Получается она не нужна вовсе, потому что в случае оседания угла здания работает арматура в верхней части и сжатая зона бетона в нижней части фундамента. А в случае проседания в середине стены начинает работать та же арматура в верхней зоне фундамента и сжатая зона роль которой выполняет вся стена целиком. А так как по вашему второму условию «чем больше высота и ширина, тем меньший диаметр арматуры можно принимать», то трещин не будет, потому что стена целиком исполняет роль очень крупной сжатой зоны, не так ли?
Надеюсь вопрос и доводы понятны, формулирую как умею)))
В целом вы все правильно сформулировали. Тем не менее сейчас для стен часто используются материалы, которые имеют значительно меньший модуль упругости, чем бетон, да и нагрузки на фундамент бывают разные, поэтому арматура в нижней зоне тоже может пригодиться.
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Источник
Как распределяется напряжение в основании. Определение несущей способности основания
Чтобы рассчитать осадку фундамента и проверить прочность (несущую способность) основания, нужно знать распределение напряжений в основании, т. е. его напряженное состояние. Необходимо иметь сведения о распределении напряжений не только по подошве фундамента, но и ниже нее, так как осадка фундамента является следствием деформации толщи грунта, расположенной под ним. Для расчета несущей способности основания также приходится определять напряжения в грунте ниже подошвы фундамента. Без этого нельзя установить наличие и размеры областей сдвигов, проверить прочность прослойки слабого грунта и т. д.
Для теоретического определения напряжений в основании используют, как правило, решения теории упругости, полученные для линейно деформируемого однородного тела. В действительности грунт не является ни линейно деформируемым, телом, так как деформации его не прямо пропорциональны давлению, ни однородным телом, так как плотность его меняется с глубиной. Однако эти два обстоятельства не сказываются существенно на распределении напряжений в основании.
В данной главе рассматриваются не все вопросы напряженного состояния оснований, а только методика определения нормальных напряжений, действующих в грунте по горизонтальным площадкам.
Распределение напряжений по подошве фундамента
В мостовом и гидротехническом строительстве, как правило, применяют жесткие фундаменты, деформациями которых можно пренебречь, поскольку они малы по сравнению с перемещениями, связанными с осадкой.
Измерения нормальных напряжений (давлений) по подошве фундамента, выполненные с помощью специальных приборов, вмонтированных на уровне подошвы, показали, что эти напряжения распределены по криволинейному закону, зависящему от формы и размеров фундамента в плане, свойств грунта, среднего давления на основание и других факторов.
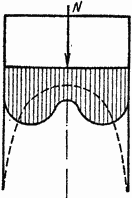
В качестве примера на рис. 2.1 сплошной линией показано фактическое распределение нормальных напряжений (эпюра нормальных напряжений) по подошве фундамента, когда нагрузка (сила N) значительно меньше несущей способности основания, а пунктиром — распределение напряжений, полученное на основе решений теории упругости.
В настоящее время, несмотря на накопленный экспериментальный материал и теоретические исследования, не представляется возможным устанавливать в каждом конкретном случае действительное распределение давлений по подошве фундамента. В связи с этим в практических расчетах исходят из прямолинейных эпюр давлений.
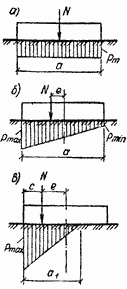
Рис. 2.2. Прямолинейные эпюры нормальных напряжений по подошве фундамента а — при центральном сжатии; б— при внецентренном сжатии и e W/AПри центральном сжатии (рис. 2.2, а) напряжения Pm, кПа, по подошве принимают равномерно распределенными и равными:
Pm = N/A, (2.1)
где N — нормальная сила в сечении по подошве фундамента, кН; А — площадь подошвы фундамента, м 2 .
При внецентренном сжатии эпюру напряжений принимают в виде трапеции (рис. 2.2, б) или треугольника (рис. 2.2, в). В первом из этих случаев наибольшее ртах и наименьшее Pmin напряжения определяются выражениями:
Pmax = N/A + M/W;
Pmin = N/A – M/W (2.2)
где M — Ne — изгибающий момент в сечении по подошве фундамента, кН·м (здесь е — эксцентриситет приложения силы N, м); W — момент сопротивления площади подошвы фундамента, м 3 .
Формулы (2.2) справедливы в случаях, когда изгибающий момент действует в вертикальной плоскости, проходящей через главную центральную ось инерции подошвы фундамента.
При подошве фундамента в виде прямоугольника с размером, перпендикулярным плоскости действия момента М, b и другим размером a имеем A = ab и W = ba2/6. Подставляя выражения A и W в формулы (2.2) и учитывая, что M = Ne, получаем:
Pmax =N/ba(1+6e/a)
Pmin=N/ba(1-6e/a) (2.3)
Напряжение Pmin, кПа, вычисленное по формуле (2.2) или (2.3) при эксцентриситете e> W/A, получается отрицательным (растягивающим). Между тем в сечении по подошве фундамента таких напряжений практически быть не может. При е> W/A край подошвы фундамента, более удаленный от силы N, поднимается под действием этой силы над грунтом. На некотором участке подошвы фундамента (со стороны этого края) контакт между фундаментом и грунтом нарушается (происходит так называемое отлипание фундамента от грунта), а потому эпюра напряжений P имеет вид треугольника (см. рис. 2.2, в). Этого обстоятельства формулы (2.2) и (2.3) не учитывают, поэтому ими нельзя пользоваться при е> W/A.
Формулы для определения размера а1, м, части подошвы, по которой сохраняется контакт фундамента с грунтом, и наибольшего напряжения Pmax, кПа (см. рис. 2.2, в), можно получить, если учесть, что напряжения P должны уравновесить силу N, кН, действующую на расстоянии с от ближайшего к этой силе края подошвы фундамента.
Отсюда вытекают два условия: 1) центр тяжести эпюры напряжений P расположен на линии действия силы N; 2) объем эпюры равен величине этой силы. Из первого условия при прямоугольной подошве фундамента следует
А1=3с, (2.4)
а из второго
(Pmax а1/2)b = N. (2.5)
Из формул (2.4) и (2.5) получаем
Pmax =2N/(3cb). (2.6)
Итак, при эксцентриситете е> W/A = a/6 наибольшее давление по прямоугольной подошве фундамента Pmax следует определять по формуле (2.6).
Источник