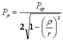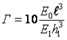Эпюра напряжения жесткого фундамента

Теоретические, фактические и расчетные эпюры напряжений под подошвой жестких фундаментов (контактная задача).

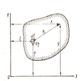
Решения Буссинеску для круглого жёсткого штампа

Контактным называют давление по подошве фундамента

Для определения контактного напряжения совместно решается два уравнения:

— Дифференциальное уравнение изогнутой оси балки;

— Физическое уравнение связей между действующим давлением и осадкой.

где: EбJб-жесткость балки

S – прогиб балки

Распределение напряжений на подошве фундамента
(Контактная задача)

Этот вопрос имеет особое значение для гибких фундаментов, рассчитываемых на изгиб.

Если известно Рконт, то загружая этой величиной фундамент, можно легко определять усилия в конструкции тела фундамента.

Из курса сопротивления материалов известно, что напряжения для сжатых конструкций при прямолинейной эпюре определяются по обобщенной формуле:

smax, min =(N/F) +-(M/W) — но здесь не учитывается работа сжимаемого основания.

Аналитическое решение по определению значений величин контактных напряжений, получено Буссинеску в виде зависимости:

Расчётная схема для решения задачи Буссинеску.

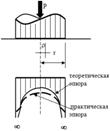
Анализируя аналитическую зависимость (см. приведённую выше формулу и схему), можно записать, что

При ρ = 0 → Рρ = 0,5Рср

и построить теоретическую эпюру контактных напряжений. Фактически же, грунт под подошвой фундамента, при давлениях, стремящихся к бесконечности (краевые точки) разрушаясь, приводит к перераспределению напряжений, возникает практическая эпюра (см. приведенную схему). Однако в данной методике также не учитываются свойства грунта основания.

При дальнейших исследованиях было установлено, что эпюра контактных напряжений под подошвой фундамента будет зависеть от его гибкости (Г) — обобщённой характеристики, учитывающей деформативные свойства основания.

Понятие гибкости (Г) было введено профессором Горбуновым-Посадовым М.И.

Е0 – модуль деформации грунта;

ℓ – полудлина фундамента (балки);

Е1 – модуль упругости материала фундамента;

h1 – высота фундамента.

Эпюры контактных напряжений под подошвой фундамента в зависимости от его гибкости. Крайняя правая схема на данном рисунке показывает, что для абсолютно жёстких фундаментов (Г=0), в целях аппроксимации, принята не фактическая седлообразная эпюра контактных напряжений, а прямоугольная (использование аппарата теории упругости к грунтам).

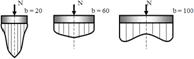
Форма эпюры контактных напряжений зависит и от ширины подошвы фундамента Р = f(b) и при прочих равных условиях (mv – const; N – const) и может быть представлена на следующей схеме:

Эпюры контактных напряжений под подошвой фундамента в зависимости от его ширины.

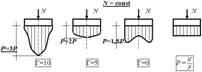
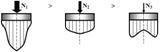
Форма эпюры контактных давлений зависит и от степени нагружения фундамента Р = f (N) и при прочих равных условиях (mv – const; F — const) может быть представлена на следующей схеме:

Эпюры контактных напряжений под подошвой фундамента в зависимости от степени нагружения.

Таким образом, приведённые примеры дают наглядную картину изменения величины и формы эпюры контактных напряжений в зависимости от поэтапного нагружения (увеличение веса сооружения в процессе его строительства), что значительно осложняет решение поставленной задачи.

Поможем написать любую работу на аналогичную тему

Теоретические, фактические и расчетные эпюры напряжений под подошвой жестких фундаментов (контактная задача).

Источник

Определение контактных напряжений по подошве сооружения

Определение контактных напряжений по подошве сооружения

При взаимодействии фундаментов и сооружений с грунтами основания на поверхности контакта возникают контактные напряжения.

Характер распределения контактных напряжений зависит от жесткости, формы и размеров фундамента или сооружения и от жесткости (податливости) грунтов основания.

Классификация фундаментов и сооружений по жесткости

Различают три случая, отражающие способность сооружения и основания к совместной деформации:

— абсолютно жесткие сооружения, когда деформируемость сооружения ничтожно мала по сравнению с деформируемостью основания и при определении контактных напряжений сооружение можно рассматривать как недеформируемое;

— абсолютно гибкие сооружения, когда деформируемость сооружения настолько велика, что оно свободно следует за деформациями основания;

— сооружения конечной жесткости, когда деформируемость сооружения соизмерима с деформируемостью основания; в этом случае они деформируются совместно, что вызывает перераспределение контактных напряжений.

Критерием оценки жесткости сооружения может служить показатель гибкости по М. И. Горбунову-Посадову

, (3.1)

где и — модули деформации грунта основания и материала конструкции; и – длина и толщина конструкции.

Модель местных упругих деформаций и упругого полупространства

При определении контактных напряжений важную роль играет выбор расчетной модели основания и метода решения контактной задачи. Наибольшее распространение в инженерной практике получили следующие модели основания:

— модель упругих деформаций;

— модель упругого полупространства.

Модель местных упругих деформаций.

Согласно этой модели, реактивное напряжение в каждой точке поверхности контакта прямо пропорционально осадке поверхности основания в той же точке, а осадки поверхности основания за пределами габаритов фундамента отсутствуют (рис. 3.1.а.):

, (3.2)

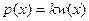
где 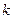– коэффициент пропорциональности¸ часто называемый коэффициентом постели, Па/м.

Модель упругого полупространства.

В этом случае поверхность грунта оседает как в пределах площади загрузки, так и за её пределами, причём кривизна прогиба зависит от механических свойств грунтов и мощности сжимаемой толщи в основании (рис. 3.1.б.):

, (3.3)

где — коэффициент жесткости основания, – координата точки поверхности, в которой определяется осадка; — координата точки приложения силы ; – постоянная интегрирования.

Влияние жесткости фундаментов на распределение контактных напряжений

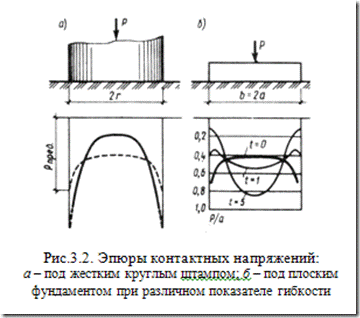
Теоретически эпюра контактных напряжений под жестким фундаментом имеет седлообразный вид с бесконечно большими значениями напряжений по краям. Однако вследствие пластических деформаций грунта в действительности контактные напряжения характеризуется более пологой кривой и у края фундамента достигает значений, соответствующих предельной несущей способности грунта (пунктирная кривая на рис. 3.2.а.)

Изменение показателя гибкости существенно сказывается на изменении характера эпюры контактных напряжений. На рис. 3.2.б. приведены контактные эпюры для случая плоской задачи при изменении показателя гибкости t от 0 (абсолютно жесткий фундамент) до 5.

Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности

Распределение напряжений в основании зависит от формы фундамента в плане. В строительстве наибольшее распространение получили ленточные, прямоугольные и круглые фундаменты. Таким образом, основное практическое значение имеет расчет напряжений для случаев плоской, пространственной и осесимметричной задач.

Напряжения в основании определяется методами теории упругости. Основание при этом рассматривается как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения.

Метод угловых точек

Метод угловых точек позволяют определить сжимающие напряжения в основании по вертикали, проходящей через любую точку поверхности. Возможны три варианта решения (рис.3.9.).

Пусть вертикаль проходит через точку , лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения как сумму угловых напряжений I и II прямоугольников, т.е.

. (3.13)

Если точка лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника. Тогда:

. (3.14)

Наконец, если точка лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой.

. (3.15)

3.3.5. Влияние формы и площади фундамента в плане

На рис. 3.10. построены эпюры нормальных напряжений по вертикальной оси, проходящей через центр квадратного фундамента при (кривая 1), ленточного фундамента (кривая 2), и тоже, шириной (кривая 3).

В случае пространственной задачи (кривая 1) напряжения с глубиной затухают значительно быстрее, чем для плоской задачи (кривая 2). Увеличение ширины, а, следовательно, и площади фундамента (кривая 3) приводит к ещё более медленному затуханию напряжений с глубиной.

3. Выбор глубины заложения фундаментов.

Глубина заложения фундаментов зависит от множества факторов, большая часть которых либо не требует особых пояснений (например, наличие или отсутствие подвалов, большие уклоны рельефа), либо играет определяющую роль только в особых случаях (например, очень большие нагрузки на основание, наличие в непосредственной близости других заглубленных сооружений, сложные инженерно-геологические условия, в том числе наличие «карманов выветривания», слоев, склонных к скольжению и т.д.). Тем не менее, имеется один фактор, над которым проектировщик вынужден задумываться практически всегда и в 90…95% принимать решение на основе именно его оценки – это глубина сезонного промерзания грунтов. Такой вопрос может не рассматриваться лишь применительно к фундаментам внутренних стен отапливаемых помещений, где глубина заложения фундаментов может приниматься без каких-либо расчетов равной 0,5м (для тонких перегородок еще меньше, например, 0,2…0,3м). В остальных случаях выбор глубины заложения фундамента начинается с установления глубины промерзания грунта.

Отечественные нормы проектирования (СНиП 2.02.01-83*, СП 50-101-2004) требуют закладывать фундаменты наружных стен не ниже расчетной глубины промерзания грунта во всех случаях, где возможно пучение грунта. Исключается такая опасность в скальных, крупнообломочных грунтах, а также в песках гравелистых, крупных и средних. В таких (непучинистых) грунтах глубина заложения фундаментов может приниматься независимо от глубины промерзания грунтов.

В мелких и пылеватых песках, в твердых супесях необходимо дополнительно учитывать наличие подземных вод: если уровень подземных вод (УПВ) ниже глубины промерзания грунта более чем на 2м, пучения можно не опасаться и закладывать фундамент, не обращая внимания на глубину промерзания. Если же УПВ выше, то глубина заложения фундамента должна быть не менее глубины промерзания грунта.

В глинах, суглинках, пластичных супесях (за исключением упоминаемого ниже случая), закладка фундаментов на глубину промерзания грунтов обязательна. Исключением являются твердые и полутвердые глинистые грунты при отсутствии подземных вод (от УПВ до нижней границы промерзания грунта более 2м), в которых глубину заложения фундамента следует принимать не менее половины глубины промерзания. Если же УПВ выше, то фундамент закладывается на полную глубину промерзания, как в остальных разновидностях глинистых грунтов. Таким образом, в большинстве случаев (70…80%) фундаменты должны закладываться на глубину, не меньшую глубины промерзания грунта.

Во всех упомянутых случаях имеется в виду расчетная глубина промерзания грунта, которая устанавливается для каждого конкретного объекта в зависимости от нормативной глубины промерзания грунтов данного района и от теплового режима здания. Нормативная глубина промерзания грунта устанавливается на основе данных гидрометеорологических служб.

Расчетная глубина промерзания грунта устанавливается путем умножения упомянутой нормативной величины на коэффициент, учитывающий влияние теплового режима сооружения. В нормах по проектированию оснований и фундаментов (СНиП 2.02.01-83*, СП 50-101-2004) приводится таблица, в которой этот коэффициент определяется в зависимости от ожидаемой температуры внутри помещения и от особенностей сооружения (вида полов, наличия подвала и т.д.). Например, при отсутствии подвала, при полах, устроенных непосредственно по грунту, при температуре внутри помещения +200С упомянутый коэффициент принимается равным 0,5, т.е. расчетная глубина промерзания будет в два раза меньше нормативной. Если полы – деревянные на лагах, то коэффициент теплового режима (в тех же условиях) будет равен 0,6.

4. Нормативная и расчетная глубина промерзания.

Расчетная

Согласно СНиП 2.02.01-83* нормативную глубину сезонного промерзания грунта d_fn, м, при отсутствии данных многолетних наблюдений следует определять на основе теплотехнических расчетов. Для районов, где глубина промерзания не превышает 2,5 м, ее нормативное значение допускается определять по формуле:

где M_t — безразмерный коэффициент, численно равный сумме абсолютных значений среднемесячных отрицательных температур за зиму в данном районе, принимаемых по СНиП по строительной климатологии и геофизике, а при отсутствии в них данных для конкретного пункта или района строительства — по результатам наблюдений гидрометеорологической станции, находящейся в аналогичных условиях с районом строительства;
Для г. M_t = 0

d₀ — величина, принимаемая равной, м, для:
суглинков и глин — 0,23;
супесей, песков мелких и пылеватых — 0,28;
песков гравелистых, крупных и средней крупности — 0,30;
крупнообломочных грунтов — 0,34.

Нормативная

Глубина промерзания грунта различна и зависит от географического места расположения.
Средняя глубина промерзания для районов следующих городов составляет:
— Волгоград, Великие Луки, Курск, Псков, Смоленск — 1,2 м;
— Санкт-Петербург, Москва, Воронеж, Новгород — 1,4 м;
— Кострома, Пенза, Саратов, Вологда -1,5 м.

Уровень подземных, грунтовых вод оказывает существенное влияние на поведение многих грунтов. Более хорошими условиями для будущего фундамента будут условия, при которых глубина промерзания меньше глубины грунтовых вод.

И, наоборот, тяжелыми условиями считаются условия, когда глубина промерзания больше глубины грунтовых вод.
В последнем случае по мере усиления морозов будет увеличиваться и глубина промерзания грунта. Когда промерзания достигнет уровня подземных грунтовых вод, начнется их превращение в лед, а вместе с этим вздутие грунта.
Это неприятное явление омрачается еще и тем, что это вспучивание практически никогда не бывает равномерным и в разных местах фундамента подъем грунта будет неравномерным. Следствие этого — перекос фундамента, перераспределение нагрузок в нем и во всем строении, возможность появления трещин, как в самом фундаменте, так и в стенах дома.
Если бы процесс шел равномерно, то проблеме вздутие грунта не следовало бы уделять столько внимания — зимой дом равномерно приподнялся, а весной равномерно опустился. К сожалению, это не достижимо и по ряду других причин.
Поэтому, если уровень грунтовых вод высок и их захватывает глубина промерзания, то есть два выхода из такой ситуации:
— учесть этот фактор при выборе надежного варианта фундамента, не считаясь с увеличением сметы на строительство;
— провести работы, если это возможно, для гарантированного понижения уровня грунтовых вод (осушение, прокладка дренажных канав и Силы, действующие на фундаменты
Рассмотрим силы, действующие на фундамент в летнее и зимнее время года при наиболее неблагоприятных условиях возведения фундамента — на пучинистом грунте с высоким уровнем грунтовых вод, расположенным выше уровня промерзания грунта.

5. Влияние конструктивных особенностей сооружения на глубину заложения фундамента.

Определение контактных напряжений по подошве сооружения

Источник