Стальные арочные покрытия больших пролетов. Общие сведения о конструкции и расчете
Арочные конструкции покрытий большепролётных зданий оказываются более выгодными по затрате материала, чем балочные и рамные системы. Однако в них возникает значительный распор, который передаётся через фундаменты на грунт или устраивается затяжка для его восприятия (т.е. погашение распора внутри системы).
Схемы и очертания арок весьма разнообразны: двухшарнирные, трёхшарнирные, бесшарнирные (см. рис. 1).
Наиболее выгодная высота арок: f=1/4 ч 1/6 пролёта L.
Высота сечения арок:
-сплошностенчатых 1/50 ч 1/80 L,
— решёточных 1/30 ч 1/60 L.
Рисунок 1 — Схемы арок.
Самыми распространёнными являются двухшарнирные арки — они экономичны по расходу материала, просты в изготовлении и монтаже легко деформируются вследствие свободного поворота в шарнирах в них не возникает значительных дополнительх напряжений от Т о и осадок опор.
В трёхшарнирных арках — всё аналогично двухшарнирным, однако ключевой шарнир осложняет конструкцию самих арок и покрытия.
Бесшарнирные арки — самые лёгкие, наиболее благоприятно происходит распределение изгибающих моментов. Однако они требуют устройства мощных фундаментов. Их нужно рассчитывать на воздействие Т о .
Сквозные арки конструируют аналогично фермам балочных схем покрытий.
Компановка каркаса и покрытия из арочных конструкций аналогична решению каркасов из рамных конструкций.
Статический расчёт арочных конструкций выполняют методами строительной механики и по специально разработанным программам на ЭВМ.
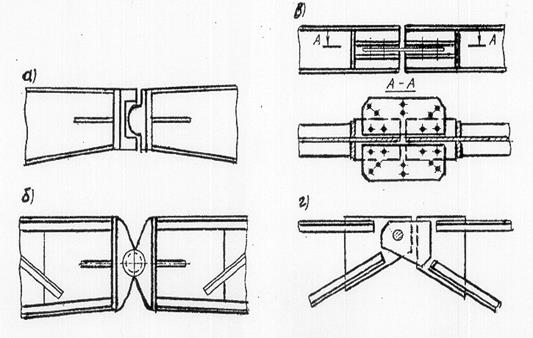
Раскосы в сквозных арках проектируют как в фермах. Наиболее сложными в конструктивном плане являются опорные и ключевые шарниры (см. рис. 2 и 3)
Рис.2 — Схемы опорных шарниров арок и рам: а — плиточный, б — пятниковый, в — балансирный: 1 — плита, 2 — цапфа, 3 —балансир).
Рис. 3 — Ключевые шарниры и арок: (а —плиточный; б —балансирный; в —листовой; г —болтовой)
Арочные конструкции рассчитывают на вертикальные (собственный вес, снег) и ветровые нагрузки. Температурные воздействия для арок обычно несущественны. Вертикальные нагрузки относят к основным сочетаниям нагрузок, ветровые и температурные воздействия – к дополнительным, величина которых при определении расчетного усилия принимается с коэффициентом сочетания nc = 0,9.
Существенной нагрузкой для арочных конструкций является давление ветра. Ветровая нагрузка для арочных покрытий, не имеющих стен, принимается по упрощенной схеме.
Расчетный коэффициент обтекания имеет положительное значение только в первой четверти дуги арки с наветренной стороны; в средней части дуги коэффициент обтекания имеет max по абсолютной величине отрицательное значение (отсос) и в последней четверти величина его резко падает, сохраняя отрицательное значение.
Ветровое давление считается приложенным нормально к поверхности арочного покрытия. Отрицательные ветровые усилия в высоких арках при малом собственном весе арки могут вызвать отрицательные опорные реакции.
Арки применяются в павильонах, крытых рынках, ангарах, спортивных залах и т.п.
По затрате металла арки оказываются значительно выгоднее, чем балочные и рамные системы. Кроме того арки просты в изготовлении и монтаже.
Расчет арок производится по правилам строительной механики, причем распор пологих двухшарнирных арок при стреле подъема не более 1/4 пролета разрешается определять в предположении наличия шарнира в ключе. Расчет арок после сбора нагрузок выполняется в следующем порядке: 1) геометрический расчет арки; 2) статический расчет; 3) подбор сечений и проверка напряжений; 4) расчет узлов арки. Нагрузки, действующие на арку, могут быть распределенными и сосредоточенными. Постоянную равномерную нагрузку g от массы покрытия и самой арки определяют с учетом шага арок. Она обычно условно считается в запас прочности, равномерно распределенной по длине пролета, для чего ее фактическое значение умножают на отношение длины арки к ее пролету S/l. Массой арки можно задаться предварительно с использованием коэффициентов собственной массы kсв=2…4, и определить его в зависимости от массы покрытия gn, снега p и других нагрузок из выражения
Снеговую нагрузку р определяют по нормам нагрузок и воздействий, условно равномерно распределенную по длине пролета покрытия. При расчете сегментных арок при f/l≥1/8 нужно учитывать также распределение снеговой нагрузки по треугольным эпюрам при значении коэффициента перехода в ключе 0, близ опор – от 1.6 до 2.2 с одной стороны и от 0.8 до 1.1 – с другой. Стрельчатые арки при определении снеговых нагрузок могут условно считаться треугольными. Ветровую нагрузку q определяют по нормам нагрузок и воздействий с учетом шага арок и считают приложенной нормально к поверхности покрытия. При этом для упрощения расчета криволинейные эпюры этой нагрузки можно заменять прямолинейными нормальными к хордам полуарок. При стрельчатых арках они условно могут считаться треугольными, и нагрузка распределится нормально к хордам полуарок. Сосредоточенные, временные нагрузки Р включают в себя массу подвесного оборудования и временных нагрузок на нем. Геометрический расчет арки заключается в определении всех размеров, углов и их тригонометрических функций полуарки, необходимых для дальнейших расчетов. Исходными данными при этом являются пролет l, высота f, а в стрельчатых арках также радиус полуарки r или ее высота f. По этим данным в треугольных арках определяют длину S/2 и угол наклона полуарки α. В сегментных арках определяют радиус
центральный угол φ из условия
и находят уравнение дуги в координатах с центром в левой опоре
В стрельчатых арках определяют угол наклона α и длину l хорды, центральный угол φ и длину S/2 полуарки, координаты центра a и b, угол наклона опорного радиуса φ0 и уравнение дуги левой полуарки . Затем половину пролета арки делят на четное число, но не менее шести равных частей и в этих сечениях определяют координаты х и у, углы наклона касательных α и их тригонометрические функции.
17. Стальные купольные покрытия больших пролетов. Общие сведения о конструкции и расчете.
Купола (рис. 102) представляют собой пологие f/D (от 1/6 до 1/10) и подъемистые (f/D от 1/2 до 1/5) оболочки двоякой кривизны с поверхностью вращения (сфера, коноид, эллипсоид, параболоид) волнистой, складчатой, сетчатой или стрельчатой конструкции на круглом плане.
Купольные конструкции принадлежат к наиболее экономичным пространственным конструкциям, применяемым в покрытиях диаметром до 150 м при толщине оболочки в 1 /600-1/800 диаметра.
Конструкции куполов бывают четырёх видов (см. рис.6): ребристые (а), ребристо-кольцевые (б), сетчатые (в), радиально-балочные (г).
Рисунок 1 — Схемы куполов
Конструкции ребристых куполов состоят из отдельных плоских или пространственных рёбер в виде балок, ферм или полуарок, расположенных в радиальном направлении и связанных между собой прогонами.
Верхние пояса рёбер образуют поверхность купола (обычно сферическую). По прогонам устраивают кровлю.
В вершине для перестыковки рёбер устраивают жёсткое кольцо, работающее на сжатие. Рёбра к центральному кольцу могут крепиться шарнирно или иметь жёсткое закрепление. Пара рёбер купола, расположенных в одной диаметральной плоскости и прерванных центральным кольцом, рассматривается как единая, например арочная, конструкция (двухшарнирная, трёхшарнирная или бесшарнирная).
Ребристые купола являются распорными системами. Распор воспринимается стенами или специальным распорным кольцом в форме окружности или многогранника с жёсткими или шарнирными сопряжениями в углах.
Между рёбрами с определённым шагом укладывают кольцевые прогоны, на которые опирается кровельный настил. Погоны, помимо своего основного назначения, обеспечивают общую устойчивость верхнего пояса ребер из плоскости, уменьшая их расчётную длину.
Для обеспечения общей жёсткости купола в плоскости прогонов устраиваются с определённым шагом скатные связи между рёбрами, а также вертикальные связи для развязки внутреннего пояса арки — между вертикальными связями устраивают распорки.
Расчётные нагрузки — собственный вес конструкции, вес оборудования и атмосферные воздействия.
Расчётными элементами купольного покрытия являются: рёбра, опорное и центральное кольцо, прогоны, скатные и вертикальные связи.
Если распор купола воспринимают распорным кольцом, то при расчёте арки кольцо может быть заменено условной затяжкой, находящейся в плоскости каждой пары полуарок (образующих плоскую арку).
В них погоны с рёбрами составляют одну жёсткую пространственную систему. В этом случае кольцевые прогоны работают не только на изгиб от нагрузки на покрытие, но и от реакций промежуточных рёбер и воспринимают растягивающие или сжимающие кольцевые усилия, возникающие от распоров в месте опирания многопролётных полуарок.
Вес рёбер (арок) в таком куполе уменьшается благодаря включению в работу кольцевых прогонов, как промежуточных опорных колец. Кольцевые рёбра в таком куполе работают так же, как и опорное кольцо в ребристом куполе, и при расчёте арок могут быть заменены условными затяжками.
При симметричной нагрузке расчет купола можно вести, расчленяя его на плоские арки с затяжками на уровне кольцевых рёбер (прогонов).
Сетчатые купола
Если в ребристом или ребристо-кольцевом куполе увеличить связность системы, то можно получить сетчатые купола с шарнирным соединением стержней в узлах.
В сетчатых куполах между рёбрами (арками) и кольцами (кольцевыми прогонами) располагают раскосы, благодаря которым усилия распределяются по поверхности купола. Стержни в этом случае работают в основном только на осевые силы, что уменьшает вес рёбер (арок) и колец.
Стержни сетчатых куполов выполняют из замкнутых профилей (круглого, квадратного или прямоугольного сечения). Узлы соединений стержней как и в структурах или сетчатых оболочках.
Расчёт сетчатых куполов производят на ЭВМ по специально разработанным программам.
Приблизительно их рассчитывают по безмоментной теории оболочек — как сплошную осесимметричную оболочку по формулам из соответствующих расчётно-теоретических справочников.
Радиально-балочные купола
Представляют собой ребристые купола, составленные из сегментных полу-ферм, расположенных радиально. В центре сегментные полуфермы присоединяются к жёсткому кольцу (решётчатому или сплошностенчатому с диафрагмами жёсткости).
Типичная форма купола — это поверхность двоякой кривизны с вертикальной осью вращения, которая может быть задана уравнением вида:
Методика расчета купола зависит от его типа и вида нагрузки — осесимметричной и неосесимметричной. К первой относится собственный вес конструкции, сплошной снеговой покров и симметрично подвешенное оборудование. Ко второй — ветровая нагрузка, односторонняя снеговая нагрузка и несимметрично расположенное оборудование. При отношении f/D ≤ 1/4 ветровой напор создает на поверхности купола отсос, который разгружает купол и может не учитываться. Однако легкие, например, пластмассовые купола необходимо проверять расчетом на действие отсоса ветра.
На стадии определения конструктивного решения тонкостенного купола применяют приближенные способы расчета. Они дают вполне достоверные результаты, зачастую с точностью выше реальных допусков, практикуемых при подборе сечений элементов купола. В рабочем проектировании пользуются точными методами, ориентированными на реализацию вычислений с помощью компьютера.
Тонкостенные купола можно рассчитывать по безмоментной теории, условиями применения которой являются: плавность изменения толщины оболочки, радиуса кривизны ее меридиана, интенсивности нагрузки; свободное перемещение оболочки в радиальном и кольцевом направлениях. Безмоментное опирание купола по внешнему контуру представляется как непрерывное, шарнирно-подвижное, образуемое стерженьками-опорами, направленными по касательным к меридиональным сечениям оболочки. В этом случае оболочка будет статически определима (рис, 9.3), При нарушении названных условий напряженное состояние купола должно определяться с учетом действия изгибающих моментов в краевых зонах.
Рисунок 2 –Схема купола с шарнорно-подвижным опиранием по контуру: а-общий вид, б- единичный элемент купола с действующим на него внутренними усилиями, в – часть купола, отделенная полностью, параллельной основанию: 1-ось вращения, 2 – шарнирно-подвижные опоры по периметру, 3 – меридиональное сечение, 4 – кольцевое сечение, 5- единичный элемент.
В безмоментном напряженном состоянии оболочка купола работает как тонкая мембрана и поэтому подвержена только нормальным усилиям, действующим в ее срединной поверхности. На практике это положение можно принять в отношении всего купола кроме приопорной зоны, где появляются изгибающие моменты.
Рассмотрим купол произвольного очертания, двоякая кривизна которого в каждой точке определяется двумя радиусами кривизны R1 и R2. В общем случае элемент оболочки купола, ограниченный двумя меридиональными и двумя кольцевыми сечениями, находится под воздействием нормальных усилий — меридионального N1 и кольцевого N2, а также касательного усилия S, отнесенных к единице длины сечения (см. рис. 9.3 а). При загружении купола осесимметричной нагрузкой (собственный вес, снег на всей поверхности) усилие S = 0, а усилия N1 и N2 определяют из условий статики как функции только угловой координаты φ (широты).
Напряженное состояние купола при осесимметричной нагрузке характеризуется следующим уравнением равновесия:
где qφ — нормальная к поверхности купола составляющая внешней нагрузки q (на 1 м2 поверхности купола).
Для определения меридионального усилия N1 кольцевым горизонтальным сечением отсекается верхняя часть купола и рассматривается ее равновесие (см. рис. 2 в). На отсеченный сегмент действует сжимающая сила Qφ, которая представляет собой сумму всех нагрузок, приложенных выше рассматриваемого сечения. Исходя из условия ΣZ=0, она должна уравновешиваться меридиональными усилиями N1 по периметру кольцевого сечения радиуса r:
где (φ—текущая угловая координата (отсчитывается от оси вращения); r = R2sinφ.
Следовательно,
Кольцевое усилие N2 находят из уравнения :
Распор купола определяется как горизонтальная проекция меридионального усилия N1
Распор в уровне опорного кольца (φ = φ0):
где N1,0 — меридиональное усилие в уровне опорного кольца; φ0 — половина центрального угла дуги оболочки в меридиональном направлении; r0 — радиус опорного кольца; Qφ,0— нагрузка, действующая на купол.
Распор Fh действует на опорное кольцо в радиальном направлении, поэтому растягивающее усилие в опорном кольце:
Сжимающее усилие в верхнем кольце от нагрузки q при соответствующей текущей координате φ определяется аналогично.
Под действием вертикальной нагрузки купол сжат, а вблизи опорного кольца растянут. Существует нейтральное кольцевое сечение («параллель»), вдоль которой усилия N2 равны нулю. Координата этой параллели определяется формой купола и видом нагрузки. Ее можно вычислить, приравняв к нулю выражение в скобках в формуле.
Дальнейшее рассмотрение оболочки вращения под действием конкретных нагрузок проведем на примере сферического купола. Геометрически он наиболее прост, а основные выводы качественного порядка, сделанные для сферы, могут быть распространены на купола других форм.
Для сферы R1 = R2 = R формулы и приобретают вид:
Формулы расчета сферических куполов на действие нагрузок от собственного веса g(кН/м2 поверхности купола) и снега s (кН/м2 перекрываемой куполом площади).
Распределение меридиональных и кольцевых усилий в полусферическом куполе от вертикальных нагрузок.
Угол φ, при котором кольцевые усилия в куполе меняют знак, превращаясь из сжимающих в растягивающие, равен
52° при действии собственного веса и 45° — при полной снеговой нагрузке. Для того, чтобы избежать растягивающих кольцевых усилий, стрела подъема купола f не должна превышать 1/52). Более подъемистые купола нуждаются в специальных кольцевых затяжках в нижних приконтурных зонах. Аналогичные вычисления усилий и критических величин углов могут быть выполнены для куполов вращения других очертаний.
При действии горизонтальных сил (ветер, сейсмика) и несимметричных нагрузок (одностороннее расположение снега) напряженное состояние купола характеризуется, кроме нормальных усилий N1 и N2, также касательными (сдвигающими) усилиями S. Расчет существенно усложняется и его выполняют по специальной методике.
Усилия N1 и N2 в гладкой оболочке купола, как правило, невелики, поэтому ее толщина определяется, главным образом, конструктивными или технологическими соображениями.
Особое внимание уделяют устойчивости купола. Формулы ее проверки, характерные для каждого материала, даются при рассмотрении особенностей куполов из различных материалов.
Волнистые и складчатые купола составляют особую группу. С архитектурной точки зрения они весьма эффектны, обладают богатой пластикой и немалыми конструктивными достоинствами, связанными с жесткостью формы. Будучи сплошностенчатыми (гладкими) или решетчатыми, они могут быть отнесены, соответственно, к тонкостенным или ребристым куполам. В железобетоне выполняют волнистые и складчатые купола, а из клееной древесины — чаще складчатые.
Источник