упругое основание в SCADe
Уважаемые завсегдатаи форума, помогите разобраться со следующей проблемой:
Осваиваю SCAD по демо-версии и при расчетах конструкций на упругом основании
(балки и плоские рамы) намеренно не ввожу какие-либо связи в узлах конструкции, желая получить
при этом неискаженную картину деформирования упругого основания.
Программа же выдает ошибку, говоря о геметрической изменяемости системы и автоматически
вводит связи сама, в результате чего постоянно получаются перекошенные деформированные
схемы, а эпюры М и Q ни разу не повторили привычные контуры, получавшиеся при
ручных расчетах (Симвулиди, Клепиков, Горбунов-Посадов, Пастернак) аналогичных конструкций.
В скудной литературе по SCADу, которая имеется у меня (учебник по SCAD, скачаный с narod.ru),
теоретический ответ на данный вопрос есть (параграф называется Парирование изменяемости),
но как практически решается этот вопрос непонятно.
С уважением, Алексей.
08.09.2005, 20:10
09.09.2005, 11:05
расчеты МКЭ и CFD. ктн
09.09.2005, 11:58
09.09.2005, 12:52
14.09.2005, 12:38
Благодарю за советы. В итоге почти все получилось. Осознал необходимость закрепления
рамы по «горизонтальным» X, Y осям именно в одной точке и именно в средней части пролета,
т.к. при закреплении по краям гасились продольные усилия в ригеле рамы, непосредственно лежащем
на у.о. Но до этого дойти не составляет труда.
При этом основной своей ошибкой считаю, неверное указание модуля деформации основания при
вычислении коэффициентов постели. Я указывал 18 МПа вместо положенных 1800000 кг/м2. Из-за
этого SCAD, по всей видимости, оценивал столь податливое основание как пустоту и
автоматически «подхватывал падающую в пустоту» конструкцию путем введения доп. связей.
Поломав SCAD на этом эффекте, выяснилось, что при значительной разнице жесткостей
между у.о. и конструкции на этом у.о., когда показатель гибкости (t) конструкции стремиться к нулю, а
жесткость конструкции соответственно стремиться к бесконечности, SCAD с определенного момента
начинает игнорировать у.о., кажущееся ему слишком «слабым» и вводит неподвижную жесткую заделку на
одной из опор. Причем, этот эффект прослеживается как при повышении жесткости балки и неизменном модуле
деформации у.о., так и при уменьшении модуля деформации у.о. при неименной жесткости балки.
При показателе гибкости t=0.0003 начинается искажение симметричной эпюры моментов балки на у.о.,
когда на одной из опор вдруг начинает возрастать опорный момент. При уменьшении t до 0.00003
эпюра моментов балки на у.о. приобретает характерное «консольное» очертание — моменты от нуля
на одной из опор возрастают до максимального значения на противоположной «защемленной» опоре.
Показатель гибкости (по Гобунову-Посадову для плокой деформации) t=10E1*L^3/(E2*h^3),
где E1 — м.д. у.о.; E2 — м.у. материала балки; L — пролет балки; h — высота сечения балки.
При нормально соотносящихся жесткостях балки и у.о. и бесконечно возрастающей нагрузке
подобного эффекта уже не наблюдается, т.е. масштаб нагрузки здесь не причем.
При этом, я так и не смог добиться от SCADa построения номальной деформированной схемы и
определения осадок в пролетных сечениях балки — SCAD вычисляет осадки (деформации) только
в узлах схемы, которые в моем случае располагались по краям балки. Попытка ввести
в пролете дополнительные узлы, принадлежащие балке, т.е. по сути дела разбить исходную
балку на несколько балочек, жестко соединенных между собой (через узлы) и одинаково
нагруженных равномерно-распределенной нагрузкой, привела к обнулению моментов во всех
средних и искажению моментов в крайних балочках.
Причем характер эпюр моментов в крайних балках говорит о том, что SCAD учел влияние группы
нагруженных средних балок путем передачи на крайние только поперечной силы, как будто
балки соединяются через шарнир. Деформированная схема показывает, что крайние балки
дают осадку с креном в сторону группы средних балок, а узлы между средними балками
оседают на одинаковую величину.
Так я и не понял как построить деф. схему исходной балки и что означает столь причудливый
характер осадок группы балок, жестко соединенных между собой.
По поводу последнего обстоятельства на ум приходят еще институтские страшилки о том,
что бесконечные (длинные) балки на у.о., загруженные равномерно-распределенной нагрузкой,
рассчитываемые по гипотезе одного коэффициента постели (Циммерман-Винклер) оседеают равномерно
без внутренних усилий в балке.
Источник
Расчет здания при сейсмике на упругом основании.
| Страница 1 из 7 | 1 | 2 | 3 | > | 7 » |
В наших (российских) нормах нет ничего на счет расчета сооружения на упругом основании при сейсмике, в них рассматривается расчет, когда схема жестко закреплена к основанию.
В различных источниках (например, в казахстанских нормах) указывается, что коэффициент постели при сейсмике должен быть увеличен в 10 раз. Понятно, что для резкого воздействия модуль упругости сильно возрастет, но почему именно 10 раз? С какого потолка взята эта цифра?
В некоторых темах форумчане пишут, что расчет конструкций при сейсмики на жестком основании идет в запас, но это совсем не так – да, уменьшаются частоты колебаний, но при этом резко увеличиваются амплитуды.
Прикладываю SCADовские модели небольшого 2х этажного здания при сейсмике 9 баллов (одна на жестком основании, другая на упругом).
Для упругого основания коэф. постели рассчитывал в связке скад-кросс, затем увеличил его в 10раз. Видно, что в схеме на упругом осн. в подвальных стенах возникают очень большие усилия ( и как следствие- нереальное армирование). Тут есть одно существенное “но”. Как понимаю, некоторые участки стен при сейсмике из-за больших гориз. воздействий начинаю работать на растяжение, т.е. некоторые фундаменты начинает отрывать от грунта, но в расчетной модели нельзя учесть, что основание может воспринимать только сжимающие усилия (в модели же пружинки постели как растягиваются так и сжимаются с одинаковым коэффициентом). Т.о. основание препятствует поднятию фундамента и в стенах возникают большие растягивающие усилия, что, по идеи, не соответствует действительности.
Фундаментную плиту, рассчитанную на упругом основании, при сейсмике вообще не представляется возможным заармировать.
Может, я что-то не понимаю и делаю неправильно (недавно столкнулся с сейсмикой)? 
Граждане, как вы рассчитываете здания при сейсмике?
Источник
Строй-справка.ру
Отопление, водоснабжение, канализация
Для гибких фундаментов, которые в основном воспринимают изгибающие моменты, образующиеся в результате совместной работы с основанием, предположение о линейном распределении реактивных давлений оказывается неприемлемым, потому что оно зависит от жесткости фундамента и податливости грунтового основания.
Замена реальной эпюры контактных давлений линейно распределенной приводит к существенным погрешностям при определении изгибающих моментов и поперечных сил.
К гибким фундаментам можно отнести ленточные и отдельные железобетонные фундаменты, а также сплошные железобетонные плиты и некоторые типы коробчатых фундаментов.
В зависимости от вида используемого фундамента различают плоскую задачу, когда условия работы поперечного сечения фундамента одинаковы по длине. Например, ленточный фундамент под стену в поперечном сечении имеет одинаковую форму деформации по всей длине.
В условиях пространственной задачи будут находиться ленточный фундамент под колонны, принимаемый в поперечном направлении жестким, и фундаментные плиты различной формы, работающие на изгиб в двух направлениях.
В настоящее время большое распространение при проектировании гибких фундаментов получили теории расчета балок и плит на упругом основании, которые справедливы для линейно деформируемых оснований, причем наибольшее применение получили следующие методы:
1) местных деформаций с постоянным и переменными коэффициентами постели;
2) упругого полупространства;
3) упругого слоя ограниченной толщины на несжимаемом основании;
4) упругого слоя с переменным модулем деформации основания по глубине.
Эти теории исходят из предположения о совместности деформации, фундамента и грунта, т. е. считается, что перемещение фундамента в данной точке контакта равно осадке поверхности грунта.
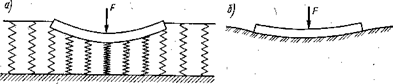
В методе местных упругих деформаций не учитываются осадки грунта основания за пределами площади загружения, что дает возможность представить такое основание в виде системы несвязанных между собой упругих пружин (рис. 7.1, а). Такие условия работы грунтового основания не подтверждаются экспериментальными данными, которые показывают, что в реальных условиях нагружения оседают не только нагруженная поверхность, но и соседние участки грунта (рис. 7.1, б). Это ограничивает область применения данного метода на практике.
Рис. 7.1. Схемы упругого основания
Метод местных упругих деформаций используют для слабых грунтов основания, для которых можно не учитывать осадки вне зоны приложения внешней нагрузки или в случае незначительной мощности деформируемого грунта, подстилаемого скальным основанием при полупролет рассчитываемого фундамента.
С целью расширения области применения данного метода для расчета гибких фундаментов стали учитывать переменное значение коэффициента постели по длине балки в зависимости от уровня действующего реактивного давления.
Метод упругого полупространства не имеет недостатков, присущих методу местных деформаций, так как он базируется на решениях классической теории упругости, рассматривающей однородные, упругие линейно деформируемые тела.
В соответствии с этими решениями осадки основания имеют место не только на участке под гибким фундаментом, но и за его пределами (рис. 7.1, б).
Однако и метод расчета гибких фундаментов при моделировании грунтового основания упругим полупространством не свободен от некоторых недостатков. В частности, экспериментальными исследованиями было доказано, что осадки за пределами площади загружения затухают значительно быстрее, чем это происходит согласно решению задачи деформирования упругого полупространства. Это связано с тем, что исходные предпосылки теории упругости могут быть применимы к грунтам только с. некоторыми ограничениями, допускающими некоторую идеализацию реальных свойств.
Наблюдения за деформациями оснований гибких фундаментов показали, что основные деформации уплотнения грунта происходят в пределах относительно небольшой глубины. Анализ результатов таких наблюдений показал, что поверхность грунта под возводимыми зданиями и гибкими фундаментами деформируется в соответствии с расчетной схемой линейно деформируемого слоя грунта, подстилаемого несжимаемым основанием.
Основная трудность при использовании этого метода заключается в том, что не всегда точно удается установить мощность сжимаемого слоя.
Источник
Фундаменты на упругом основании
Особенности расчёта фундаментов на упругом основании.
На практике встречаются случаи, когда фундаменты зданий должны не только передать нагрузку на основание при условии недопущения возникновения значительых его осадок, но и обеспечить уменьшение неравновномерности осадок до допустимых значений, установленых для данного типа сооружения. В этих случаях нагрузку от группы колонн или стен передают на один фундамент, устраивая его ленточным или в виде плиты. Такие фундаменты, воспринимая изгибающие усилия, позволяют частично выравнивать осадку. Ленточные фундаменты под колонны в целях уменьшения неравномерности осадки не только отдельных колонн в ряду, но и здания в целом, иногда устраивают в виде перекрестных лент. Расчет ленточных фундаментов под стены зданий был рассмотрен ранее в гл. 2 данного учебного пособия. Однако их расчет, например, под колонны зданий, имеет существенные отличия,
В настоящее время известно множество методов расчета фундаментов на упругом основании, которые имеют свои преимущества и недостатки. Остановимся на методе И. А. Симвулиди, как одном из наиболее удобных с инженерной точки зрения.
При выводе расчетных формул в данном методе расчета использованы уравнения плоской задачи теории упругости. Грунт основания считается сплошной однородной упругой средой, характеризуемой модулем общей деформации и коэффициентом поперечной деформации. И. А. Симвулиди использовал дифференциальное уравнение четвертого порядка упругой линии балки:
(13.1)
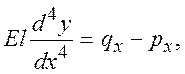
где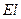 
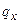
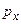
– жесткость балки; 
– внешняя нагрузка, приложенная к балке; 
– реакция грунта.
Реактивное давление грунта на балку принимается в виде алгебраического полинома с четырьмя неизвестными параметрами:
(13.2)
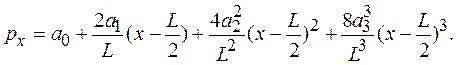
Для определения неизвестных параметров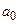 
, 
, 
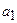
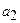
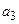
и 
необходимо совместное рассмотрение уравнений с последующим четырехкратным интегрированием выражения.
В результате интегрирования и рассмотрения восьми граничных условий получены общие формулы для определения реактивного давления грунта под балкой, поперечных сил и изгибающих моментов. Следует отметить, что конечные формулы в общем, виде представляют собой очень сложные математические зависимости. Однако эти формулы упрощены до степени, доступной проектировщику в его практической работе, для чего составлены специальные таблицы, значительно снижающие трудоемкость расчетной работы.
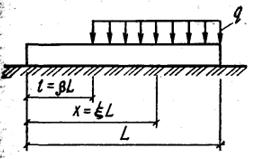
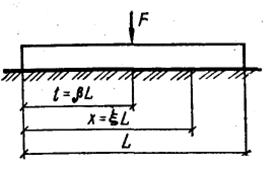
| Рис. 13.1. Схема загружения балки равномерно распределенной нагрузкой | Рис. 13.2. Схема загружения балки сосредоточенной силой |
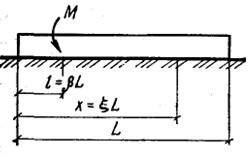
Рис. 13.3. Схема загружения балки сосредоточенным изгибающим моментом
Для использования таблиц необходимо знать показатель гибкости:
(13.3)
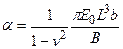
где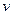 
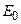
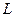
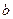
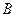
– коэффициент поперечных деформаций грунта; 
– модуль общей деформации грунта; 
– длина балки; 
– ширина поперечного сечения балки; 
– жесткость балки.
Необходимые данные для расчета гибких фундаментов, загруженных равномерно распределенной нагрузкой (рис. 13.1), приведены в таблицах. С помощью таблиц вычисляют реакцию грунта по подошве балки, поперечную силу и изгибающие моменты. В случае если балка загружена системой сил, то суммарные усилия можно найти, используя принцип независимости действия сил в результате сложения ординат одноименных усилий.
Армирование фундаментов на упругом основании осуществляется в соответствии с правилами армирования изгибаемых железобетонных конструкций, подробно изложенными в курсе строительных конструкций.
Дата добавления: 2014-05-28 ; просмотров: 787 ; Нарушение авторских прав
Источник