Как называется наружный угол образуемый сопряжением двух стен

Сопряжение несущих стен

Важным конструкционным элементом здания являются внутренние несущие стены. Они через фундамент вместе с наружными стенами передают нагрузки на грунт.

Правильное выполнение этой функции возможно лишь при условии их правильного сопряжения. От качества сопряжения несущих стен зависит статичность конструкции всего дома. Несущие стены одного этажа желательно выполнять из элементов — одинаковой прочности, возводя их равномерно по всему периметру.

Иногда внутренние несущие стены возводятся из иных материалов, нежели наружные. В таком случае они соединяются встык с помощью анкеров. Сопряжение стен обеспечивается не менее чем пятью полосами железа сечением 3х 30 мм, которые заводятся внутрь находящихся на одном уровне швов в кладке соединяемых стен.

Это условие достаточно легко соблюдать, если наружные стены имеют слоистую структуру. Как правило, в этом случае их несущий слой проектируется из тех же пустотелых кирпичей или блоков, что и внутренние конструкционные стены.

Одновременно с кладкой обеих стен выполняется соответствующая перевязка их элементов — пустотелые кирпичи или блоки каждого второго слоя внутренней стены входят в наружную стену на всю ее толщину. Такое соединение является наиболее надежным.

Eсли часть несущих стен кладется позднее, можно соединить их с теми стенами, что уже возведены, при помощи так называемых штраб.

В этом случае из каждого второго ряда выдвигаются элементы кладки, которые делают возможным возведение и привязку новых стен. В наружной стене можно оставить «гнезда», а позднее достроить внутреннюю стену, вмуровывая ее во внешнюю

Если наружная стена является однослойной (однородной), то очень важным условием, кроме прочности такого соединения, является отсутствие «мостиков холода».

При строительстве из ячеистого бетона для возведения однослойных наружных стен используются блоки марки М400, а для внутренних несущих стен — марки М600. Нужно сказать, что бетон более высоких марок является более прочным, но, к сожалению, и более «холодным». Следовательно, обе стены нужно возводить несколько иначе.

Подобные требования распространяются и на сопряжения стен из пористой керамики. Сопряжение должно быть соответствующим образом утеплено, поскольку для кладки внутренних стен используются пустотелые блоки с меньшей степенью пористости, следовательно, несколько более «холодные».

Несущие стены одного этажа — наружные и внутренние — в принципе соединяются только при помощи перевязки кладки. Чтобы однослойные наружные стены были теплыми, толщина кладки, как правило, должна составлять 36 см (ячеистый бетон) или 44 см (поризованная керамика).

Такие толстые стены с легкостью переносят нагрузки от верхнего этажа. Несущие внутренние стены на 12-19 см уже, поэтому часто они кладутся из более прочных, но, к сожалению, и более «холодных» материалов.

Источник

Сопряжения

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

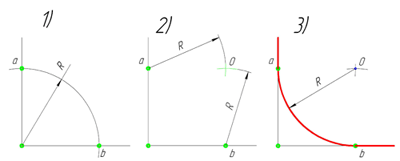
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
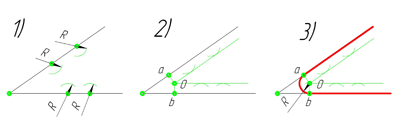
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

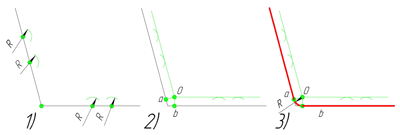
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Сопряжение параллельных прямых линий

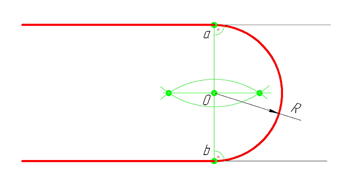
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

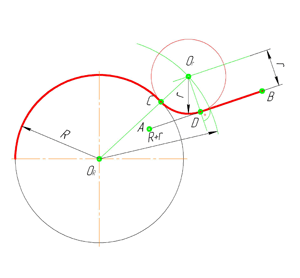
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .

Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

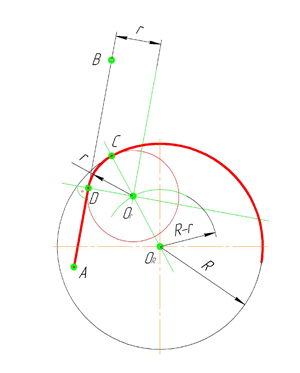
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

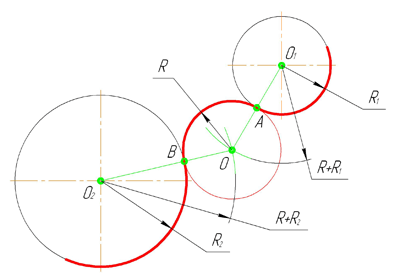
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

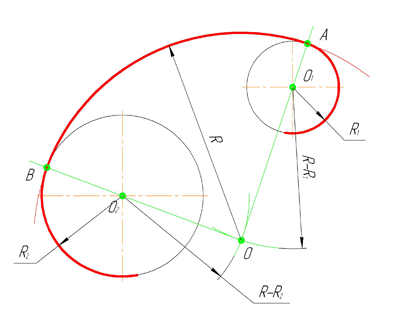
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Источник

Как называется наружный угол образуемый сопряжением двух стен

С течением времени накрывка подсыхает и с трудом затирается. Чтобы сделать ее мягче, затираемую поверхность штукатурки смачивают водой с помощью кисти.

При затирке вкруговую остаются слегка заметные кругообразные следы. Поэтому при высококачественных отделках затирку вкруговую дополняют затиркой вразгонку.

Терку, хорошо очищенную от раствора, плотно прижимают к поверхности и начинают производить ею прямолинейные движения – взмахи. Таким образом устраняют все следы от затирки вкруговую.

Если поверхность штукатурки, затертая вкруговую, высохла, то ее смачивают водой, а затем затирают вразгонку.

Наибольшая чистота затертой штукатурки достигается, когда работу выполняют сначала деревянной теркой, а затем теркой, полотно которой обито войлоком и фетром.

Заглаживание . Заглаживание выполняют двумя способами. В первом случае нанесенную накрывку сначала разравнивают деревянным полутерком, а затем заглаживают гладилкой в одном или в двух направлениях.

На стенах накрывку сначала заглаживают в вертикальном направлении от пола к потолку, а затем в горизонтальном по длине или ширине пола.

На потолке сначала заглаживание выполняют поперек лучей света, идущих из окон, а затем по их направлению.

Во втором случае одновременно намазывают и разравнивают накрывочный раствор, а затем заглаживают его.

При заглаживании работу лучше выполнять вдвоем. Один наносит раствор и разравнивает его, другой заглаживает.

При заглаживании гладилкой, обитой резиной, поверхности имеют вид мелкопесчаных фактур. Такую поверхность лучше окрашивать клеевыми красками. При заглаживании металлическими гладилками поверхность штукатурки становится как бы железненной. Ее лучше окрашивать масляными красками.

Лузги, усенки и фаски

Лузг – внутренний угол в местах примыкания двух стен или потолка и стены; усенок – наружный угол, образуемый в местах сопряжения двух стен. Так как острые углы (усенки) быстро обламываются, их притупляют, закругляя или снимая фаски .

Натирка и разделка лузгов, усенков и фасок – трудоемкие операции. Лузги, усенки и фаски выполняют лузговым или усеночным правилами, полутерками, шаблоном.

Для натирки лузгов или усенков используют растворы, приготовленные на мелком просеянном песке. К нанесенному раствору прикладывают лузговое или усеночное правило и, передвигая его с небольшим нажимом вверх и вниз, натирают до получения точной чистой линии лузга или усенка. Эти элементы должны быть выполнены строго вертикально или горизонтально.

Дефекты исправляют маленькими полутерками с дополнительным нанесением раствора в нужные места.

Фаски натирают по ранее выполненным усенкам. Для этого готовые усенки смачивают водой, с торца к ним прикладывают полутерок и, передвигая его с небольшим нажимом вверх и вниз, растирают раствор усенка в одной плоскости или закругляют его.

Лузги и усенки вытягивают также по двум навешенным правилам. Так как навешивание правил занимает много времени, то используют шаблоны из скрепленных вместе двух профильных досок, которые передвигают по маячной раме, изготовленной из двух уголков, скрепленных под углом. В этом случае навешивают не отдельные правила, а целую раму, что повышает производительность труда. Однако шаблон и маячная рама образуют только прямой угол. Для получения тупого или острого угла приходится исправлять вручную одну сторону лузга, усенка или фаски, затрачивая дополнительное время. Шарнирный шаблон с раздвижной профильной доской позволяет вытягивать лузги, усенки и фаски с разными углами без дополнительной подправки.

Механизированное нанесение и разравнивание раствора

Нанесение раствора . Перед нанесением растворы процеживают через сита. Подвижность раствора для обрызга и грунта без гипсового вяжущего – 6–10 см, для накрывочного слоя, содержащего гипсовое вяжущее, – 9–12 см, без вяжущего – 7–8 см. Растворы с осадкой конуса 10–12 см наносят механическими форсунками, с осадкой конуса 7–9 см – пневматическими.

Во время нанесения раствора обрызга и грунта форсунки держат к оштукатриваемой поверхности под углом 60–90°, при нанесении обрызга по драни

– под углом 60°. Раствор наносят движениями сверху вниз и слоями следующей толщины: для обрызга по деревянным поверхностям – не более 9 мм, по каменным, кирпичным, бетонным поверхностям – не более 5 мм. Слой грунта не должен превышать 8 мм при известково-гипсовых растворах, 7 мм – при известковых и цементно-известковых растворах, 5 мм – при цементных растворах. Чтобы раствор не сползал при повторном нанесении, предыдущий слой раствора должен отвердеть.

Источник