Как обеспечить жесткость стыка колонны с фундаментом

Расчёт узла сопряжения колонн с фундаментом

Рубрика: Технические науки

Дата публикации: 28.05.2015 2015-05-28

Статья просмотрена: 12746 раз

Библиографическое описание:

Абрашитов, В. С. Расчёт узла сопряжения колонн с фундаментом / В. С. Абрашитов, А. Н. Жуков, Э. Х. Алмаметов. — Текст : непосредственный // Молодой ученый. — 2015. — № 11 (91). — С. 213-217. — URL: https://moluch.ru/archive/91/19612/ (дата обращения: 19.08.2021).

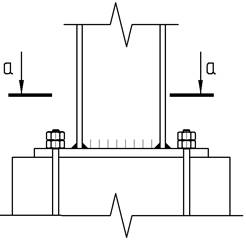
Одной из основных задач при проектировании стальных рамных каркасов многопролётных зданий является закрепление колонны в фундаменте, обеспечивающее восприятие поперечной и продольной сил, а также изгибающего момента расчетной величины при основном и особом сочетании нагрузок.

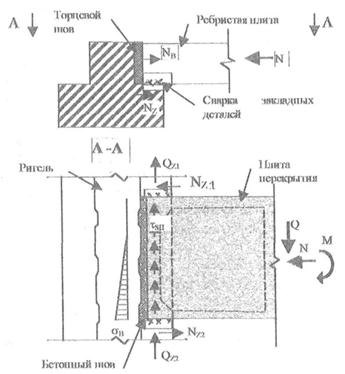
В соответствии с расчётной схемой металлического каркаса многопролётного здания имеется в узлах соединения колонны с фундаментом либо шарнирное, либо жёсткое сопряжение (рис.1).

Рис.1. Узел соединения колонны с фундаментом

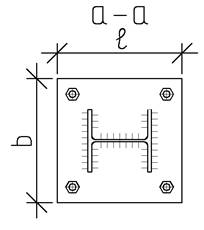
При анализе проектной документации нескольких зданий для Пензы и Пензенской области выявлено, что соединение металлической колонны из прокатного двутавра с железобетонным столбчатым фундаментом осуществляется через металлическую базу из плиты базы и четырёх анкерных болтов (рис. 2). Причём анализируемые проекты имели здания с несколькими пролетами и высотой не менее трёх этажей. Соединения несущих балок с колонной осуществлено по шарнирной схеме. Естественно, что при определении усилий в элементах поперечной рамы необходимо было вводить жёсткое соединение фундамента с колонной в виде жёсткого закрепления, так как в противном случае система становится статически изменяемой (при шарнирном соединении колонн с фундаментом). В рабочей же документации показывается узел соединения колонны с фундаментом через плоскую плиту и четыре анкерных болта.

Рис. 2. Соединение колонн с железобетонным фундаментом

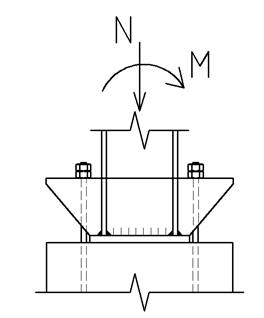
Вместе с тем базы колонн имеют закрепления нижнего конца в фундаменте либо шарнирное, либо жёсткое. Причём если колонны центрально сжаты, то крепления их к фундаментам можно осуществлять непосредственно за опорную плиту болтами, чаще всего двумя и иногда четырьмя, которые условно можно назвать монтажными. При этом такое закрепление называют шарнирным, так как на плиту базы не действует изгибающий момент (М=0). Анкерные болты должны воспринимать изгибающие моменты и работать, как правило, на растяжение, что приводит к тому, что база проектируется с наличием распределительных траверс по схеме на рис.3, то есть жёсткой.

Рис. 3. Жёстко опёртая база внецентренно-сжатой колонны

Напряжение под плитой базы колонны определяется в зависимости от величины значений N и M по формуле:

,

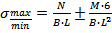
где В — ширина плиты базы, а L — длина базы.

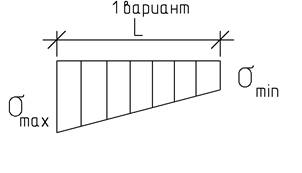
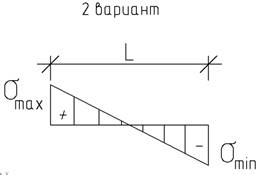
Значения этих напряжений могут быть разные в виде схем (рис.4):

Рис.4 Эпюры нагружения

Анализируя оба варианта эпюр нагружения, можно сказать, что по первому варианту болты не работают на растяжение и их условно можно назвать монтажными, так как они работают на сжатие.

По второму варианту контактная зона плиты с фундаментом не может воспринимать растягивающие напряжения и растягивающие усилия, воспринимаемые анкерными болтами. Сила, которую воспринимают анкерные болты, определяется из условия статического равновесия системы по формуле:

,

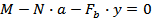
где M и N — расчётные усилия для фундаментной плиты; 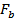— сила, которую воспринимают анкерные болты; a — расстояние от центра тяжести плиты базы до центра тяжести эпюры сжатых напряжений под плитой базы; y — расстояние от анкерных болтов до центра тяжести эпюры сжатых напряжений.

Чем меньше будет значение продольной силы и больше значение изгибающего момента, тем больше будет значение силы 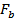. Выполняя соединение колонны с плитой базы по рисунку 1 это соединение в технической литературе [1], [2], [3] всегда считалось шарнирно опёртым. Тем не менее, имеется техническое решение по типовой серии 1.423.3–8 вып.2, когда базу колонн проектируют без траверс для бескаркасных зданий, в зданиях с подвесным транспортом и с мостовыми кранами общего назначения грузоподъемностью до 5 тс. Такая плита базы должна быть рассчитана на изгиб по схеме на рис.5.

Рис.5 Схема грузовой площади при расчёте плиты базы на изгиб от отпора фундамента на плиту

Расчет плиты ведут по следующей методике, описанной в [5]:

Толщину опорной плиты следует определять расчетом на изгиб пластинки по формуле

(1)

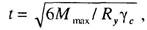
где М_max — наибольший из изгибающих моментов М, действующих на разных участках опорной плиты и определяемых по формулам:

1) для консольного участка плиты

(2)

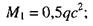
2) для участка плиты, опертого на четыре стороны в направлении короткой и длинной сторон соответственно

(3)

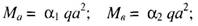
3) для участка плиты, опертого по трем сторонам

(4)

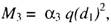
для участка плиты, опертого на две стороны, сходящиеся под углом, по формуле (4), принимая при этом d₁ — диагональ прямоугольника, а размер а₁ в таблице Е.2 [5]- расстояние от вершины угла до диагонали. Здесь с — вылет консольного участка плиты;

α₁, α₂, α₃ — коэффициенты, зависящие от условий опирания и отношения размеров сторон участка плиты и принимаемые согласно таблице Е.2 [5]; q — реактивный отпор фундамента под рассматриваемым участком плиты на единицу площади плиты.

При этом площадь стальной опорной плиты должна удовлетворять требованиям расчета на прочность фундамента. Передача расчетного усилия на опорную плиту может осуществляться через фрезерованный торец или через сварные швы конструкции, опирающейся на плиту [5].

В связи с этим необходимо рассчитать сварной шов, прикрепляющий плиту базы к сплошной колонне, применяя для этого формулу:

, (5)

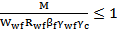
где 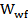— момент сопротивления расчётного сечения сварного соединения по металлическому шву.

Данная формула применяется, если значение 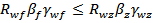; то есть расчёт ведётся по металлу шва, а не по металлу границы сплавления (см. [5]).

Только если толщина плиты и сварные соединения колонны с плитой удовлетворяют вышеуказанным расчётам, можно считать соединение колонн с фундаментом по рисунку 1 условно жёстким и в расчётах опорный узел принимать жёстким. При проверке несущей способности уже изготовленных рам с устройством соединения колонн с фундаментом по типу рис. 1 без траверс нельзя считать соединения жесткими.

1. Металлические конструкции. Под ред. Н. С. Стрелецкого, М., 1961.

2. Муханов К. К. Металлические конструкции. М. Строиздат, 1967.

3. Васильев А. А. Металлические конструкции. М. Строиздат, 1975.

4. Металлические конструкции. Справочник проектировщика, Т. 2. Под ред. В. В. Кузнецова, М., 2011.

5. СП. 16. 13330. 2011. Стальные конструкции. Актуализированная редакция. СНиП II-23–81*. М., 2011.

Источник

ПРЕДИСЛОВИЕ

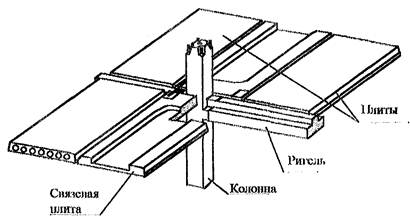
Каркасные здания промышленного и гражданского назначения являются массовыми конструктивными системами. Они получили распространение благодаря широким возможностям вариаций объемно-планировочных решений внутреннего пространства, а также за счет полной индустриализации изготовления и монтажа конструкций, дифференциации несущих и ограждающих элементов по назначению, что позволяет с использованием системы унификации и типизации эффективно распределять материалы и сократить их общий расход.

Особенностью каркасов многоэтажных зданий из сборного железобетона является большое количество узловых сопряжений, которые в соответствии с принятой системой разрезки здания на элементы, располагаются, как правило, в наиболее напряженных зонах [8, 22, 24, 28, 34, 35, 39]. При этом для стыков сборных элементов характерна повышенная деформативность вследствие обмятия бетона по контактным поверхностям и трещинообразования, податливости сварных соединений арматуры и закладных деталей [2, 3, 4, 8, 9, 11, 12, 25, 37]. Кроме того, в узловых сопряжениях в большей степени проявляется физическая и конструктивная нелинейность и их податливость меняется в зависимости от напряженно-деформированного состояния [3, 9, 14, 21, 26]. Экспериментальные исследования показывают, что переменная податливость сопряжений приводит к существенному (до 40 %) перераспределению усилий [20, 41].

В существующих методах расчета пока не в полной мере учитывается влияние податливости узловых сопряжений на совместную работу несущих подсистем каркасных зданий — продольных и поперечных рам, дисков перекрытия и диафрагм жесткости. В основном это объясняется недостаточной изученностью пространственного взаимодействия сборных элементов как в упругой, так и в пластической стадиях работы [1, 7, 23, 32, 33]. Поэтому, как правило, расчет каркасных зданий производится по расчетным схемам с шарнирными или жесткими узлами сопряжений элементов, что не всегда адекватно отражает работу конструкции. При современных повышенных требованиях к экономической эффективности конструктивных решений исследования по дальнейшему уточнению расчетных схем приобретают особую актуальность.

Благодаря интенсивному развитию вычислительной техники и программного обеспечения, реализующих численные методы расчета (в основном, метод конечных элементов), стало возможным моделировать сложные процессы взаимодействия и проводить вычисления по пространственным расчетным схемам с требуемой точностью. Однако, для адекватного описания напряженно-деформированного состояния необходимо опираться на общие физические закономерности работы сопряжений различной конструкции, в которых до настоящего времени еще ощущается недостаток.

В рекомендациях предложена методика оценки податливости сопряжений сборных железобетонных конструкций, основанная на обширных экспериментальных исследованиях ряда авторов. Даны рекомендации по составлению расчетных схем каркасов многоэтажных зданий, в которых моделируется податливость сопряжений стержневых и плоскостных элементов здания. При этом учитывается физическая и конструктивная нелинейность сопряжений.

Вследствие сложности напряженно-деформированного состояния и большого количества конструктивных факторов, влияющих на пространственную работу сопряжений, рекомендации применимы к конкретным конструктивным решениям массового применения.

1. ОБЩИЕ ПОЛОЖЕНИЯ

1 .1. Настоящие рекомендации применимы при расчете связевых, рамных и комбинированных каркасов многоэтажных зданий с конструкциями вертикальных элементов жесткости в виде стальных решетчатых связей, сплошных и с проемами железобетонных диафрагм с переменными по высоте характеристиками.

1 .2. Рекомендации могут быть использованы при расчете каркасов, воспринимающих особые нагрузки и воздействия (действие сейсмических и кратковременных динамических нагрузок, проектирование зданий на просадочных основаниях).

1.3 . В рекомендациях излагается метод определения податливости сопряжений сборных железобетонных конструкций для формирования плоских и пространственных расчетных моделей каркасов многоэтажных зданий при расчете методом конечных элементов, который также может быть использован при расчете конструкций другими численными и аналитическими методами.

1 .4. Под податливостью стыка понимается повышенная деформативность соединения на малом, по отношению к высоте сечения, участке длины стыка по сравнению с деформативностью стыкуемых элементов. По физической сути податливость соединения равна смещению, вызванное единичной силой — при сжатии-растяжении, сдвиге или повороте.

1.5 . Деформативность (в дальнейшем податливость) стыков несущих элементов каркаса — колонн, ригелей, плит перекрытий, элементов диафрагм жесткости и фундаментов может быть вызвана следующими факторами: снижение расчетных стыкуемых площадей конструкций для обеспечения соединений арматуры; обмятие бетона конструкций и шва по контактным поверхностям и развитие, вследствие этого, неупругих деформаций; пониженная трещиностойкость и сопротивляемость развитию трещин бетона шва; податливость сварных соединений арматуры и закладных деталей и т.д.

1.6 . При изменении напряженно-деформированного состояния узлового сопряжения вследствие проявления физической и конструктивной нелинейности податливость сопряжения изменяется.

1.7 . В расчетах конструкций при определении податливости рекомендуется использовать так называемый коэффициент жесткости стыка, который определяется как тангенс угла наклона секущей к кривой на диаграмме усилие — перемещение для стыка.

1 .8. Следует различать линейную, угловую и сдвиговую податливость, которые зависят от соответствующих деформаций. Линейная податливость (1/ C _х , 1/ C _y , 1/ C_z ) обусловлена деформациями растяжения-сжатия и характеризуется зависимостью « N — δ ». Сдвиговая податливость (1/С_γ) обусловлена деформациями сдвига при действии поперечной силы и характеризуется зависимостью « Q — γ ». Угловая податливость (1/С_φ) обусловлена деформациями поворота при действии изгибающего или крутящего момента и характеризуется зависимостью «М — φ». Здесь приняты обозначения: N, Q и М — продольная, поперечная сила и изгибающий момент в сечении стыка соответственно; δ , γ и φ — продольная деформация, угол сдвига и угол поворота в сечении стыка; С _х , С _γ и С_φ коэффициенты линейной, сдвиговой и угловой жесткости (усилия, вызывающие единичные деформации).

2. КОНСТРУКТИВНЫЕ РЕШЕНИЯ УЗЛОВЫХ СОПРЯЖЕНИЙ СБОРНЫХ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ КАРКАСНЫХ ЗДАНИЙ

2.1. Общие требования

2 .1.1. Каркас здания должен работать под нагрузкой как единая пространственная система. В связи с этим к сопряжениям сборных железобетонных конструкций предъявляется комплекс требований:

— прочность стыка должна быть не ниже стыкуемых элементов для исключения преждевременного разрушения конструкции как в стадии монтажа, так и при воздействии эксплуатационных нагрузок;

— жесткость стыка должна обеспечивать передачу расчетных усилий сопряженных элементов, неизменяемость их взаимного положения, нормируемые перемещения элементов под нагрузкой и пространственную жесткость здания в целом.

Кроме того стыки должны быть по возможности универсальными, технологичными при монтаже, обеспечивать правильность соединения элементов и располагаться в зонах с минимальными усилиями.

2 .1.2. Связь стыкуемых железобетонных элементов обеспечивается следующими образом: для восприятия растягивающих усилий производится сварка арматурных стержней или закладных деталей; для восприятия сжимающих усилий, в дополнение к сварным соединениям, швы между элементами омоноличиваются; для передачи сдвигающих усилий выполняются сварные соединения и устраиваются бетонные шпонки.

2.2. Вертикальные стыки колонн

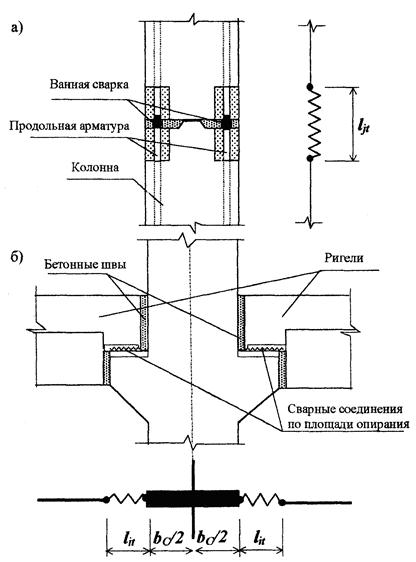
2.2.1 . Вертикальные стыки колонн по расчетно-конструктивному признаку относят к стыкам, работающим на внецентренное сжатие, которые рекомендуется размещать в зонах с минимальными изгибающими моментами. Требования к вертикальным стыкам заключаются в обеспечении соосной передачи продольных усилий и распределения концентрированных сжимающих напряжений по сечению. Стыки колонн могут быть шарнирными (контактными), т.е. воспринимающими только продольные и поперечные силы или жесткими, рассчитанными, в дополнение к сказанному, на восприятие изгибающих моментов. Пример конструкции стыков показан на рис. 1 .

2 .2.2. Податливость стыков колонн может быть вызвана рядом причин: концентрацией сжимающих напряжений из-за уменьшенной расчетной площади и неровностью контактной поверхности стыкуемых элементов; наличием растворных швов меньшей прочности; повышенной деформативностью сварных соединений продольной арматуры (рис. 1 , в). При размещении стыков в зоне с минимальными изгибающими моментами рекомендуется учитывать только линейную податливость.

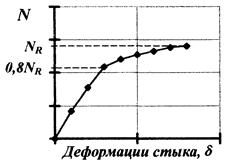
2.2.3 . Податливость стыков колонн с ростом нагрузки повышается за счет развития неупругих деформаций в элементах соединения. Интенсивное повышение деформативности стыка проявляется на этапах уровней нагрузки 0,6 — 0,8 N _R ( N _R — разрушающая нагрузка).

Длина зоны повышенной деформативности зависит от конструкции стыка и определяется, как правило, участком с уменьшенным поперечным сечением (рис. 1, в).

Рис. 1 . Вертикальные стыки колонн:

а) жесткий, со сваркой продольной арматуры; б) шарнирный без соединений по продольной арматуре; в) стык в сборке и эпюра распределения продольных деформаций

2.3. Сопряжения сборного перекрытия с колонной

2.3.1 . Сопряжение перекрытия с колонной (рис. 2 ) должно обеспечивать передачу вертикальных и горизонтальных нагрузок от перекрытия на колоны и, при необходимости, пространственную жесткость каркаса. В сопряжении балочного перекрытия с колонной основным стыком, определяющим расчетную схему каркаса является стык ригеля с колонной. При наличии вертикальных элементов жесткости стык межколонных (связевых) плит перекрытия с колонной оказывает меньшее влияние на статическую схему работы каркаса.

Рис . 2. Сопряжение колонны со сборным перекрытием

2.3.2 . Стыки ригеля с колонной принято различать шарнирные — для связевых каркасов и жесткие — для рамных каркасов. В большинстве конструктивных решений ригель опирает ся на устроенные в колоннах короткие консоли (рис. 3 , 4 ).

2.3.3 . В связевых каркасах стык ригеля с колонной рассчитывается на восприятие вертикальных нагрузок и горизонтальных нагрузок, возникающих в период монтажа.

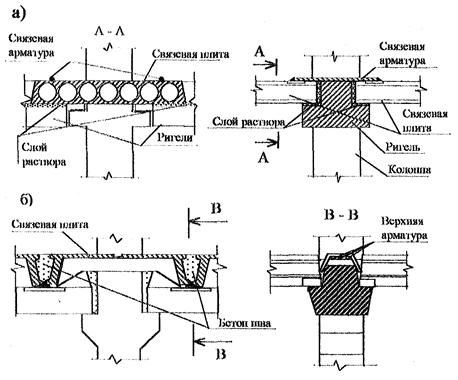
Рис. 3 . Конструкции сопряжений ригеля с колонной и связевом каркасе:

а) со скрытой консолью и верхней монтажной соединительной пластиной; б) со скрытой прямоугольной консолью; в) схема распределения усилий при действии горизонтальной нагрузки

Рис. 4 . Рамный узел сопряжение ригеля с колонной:

а) с опиранием на открытую консоль; б) с опиранием на скрытую консоль; в) график зависимости угла податливости сопряжения от изгибающего момент а

В соединении ригеля с колонной производится сварка опорных закладных деталей понизу и приварка поверху стальных пластин или арматурных стержней (рис. 3, а). В верхнем соединении, как правило, используются мягкие стали для обеспечения восприятия фиксированного изгибающего момента величиной до 10 — 20 % от пролетного, в основном в период монтажа.

Величина момента на опоре зависит от направления действия нагрузки. Особенно это проявляется при незамоноличенных швах. В растянутых элементах (пластинках, арматурных стержнях) при расчетных максимальных нагрузках допускаются напряжения соответствующие пределу текучести, что приводит к возникновению остаточных деформаций и, в итоге, к повышению деформативности узла при знакопеременных временных нагрузках по сравнению с начальным значением.

2.3.4 . В узлах сопряжения ригеля с колонной связевого каркаса без монтажных соединений по верхней зоне (рис. 3 , б) после сварки опорных закладных деталей и омоноличивания швов наряду с сопротивлением сжатию-растяжению возникает сопротивление повороту ригеля относительно колонны, т.е. имеет место частичное защемление колонны в диске перекрытия.

Дли сопряжений рис. 3 защемление носит односторонний характер. При действии изгибающего момента в сторону пролета узел «раскрывается» (рис. 3, в) и опорные моменты малы поскольку на изгиб работают только опорные закладные де тали, при действии изгибающего момента в другом направлении происходит обжатие шва омоноличивания и возникает пара сил (рис. 3, в). Поскольку опорные закладные детали обладают податливостью, а бетон омоноличивания, как правило, имеет более низкую прочность чем бетон сопрягаемых конструкций, то узел обладает меньшей изгибной жесткостью чем сечения ригеля.

2.3 .5. В рамных сопряжениях (рис. 4 ) верхняя арматура устанавливается по расчету для восприятия суммарного изгибающего момента от расчетных вертикальных и горизонтальных нагрузок. Соединение между ригелем и колонной осуществляется сваркой опорных закладных деталей, а в верхней зоне выполняется приварка стальных пластин накладок или арматурных стержней к закладным деталям или к выпускам арматуры колонн и ригелей.

Для боль шинства конструкций стыков величина сопротивления зависит от направления действия изгибающего момента, продольных и поперечных сил.

2.3 .6. Податливость рамного сопряжения вызывается повышенной деформативностью опорных закладных деталей и сварных соединений арматуры. Кроме того, податливость сопряжения может быть вызвана развитием неупругих и накоплением остаточных деформаций в элементах соединений, что особенно проявляется при нагрузках, превышающих (0,3 ÷ 0,4) M_r (где M_r — предельный момент по несущей способности рамного узла сопряжения), как это показано на рис. 4 , в.

2 .3.7. В направлении вдоль пролетов плит сопряжение перекрытия с колонной в большинстве случаев принимается шарнирным. Частичное защемление колонн в перекрытии проявляется по линии расположения связевых плит-распорок, имеющих продольные сварные соединения (рис. 5 , а) и при устройстве перекрытия из ребристых плит, привариваемых по опорным площадкам к закладным деталям ригеля (рис. 5 , б). Механизм возникновения сопротивления при повороте опорного сечения плит относительно ригеля и колонны аналогичен описанному в п.п. 2.3.3 — 2.3.4 (рис. 3 , в).

2.4. Стык колонны с фундаментом

2.4 .1. Работа стыка колонны с фундаментом зависит от конструкции фундамента — сплошной или столбчатый, в сборном или монолитном исполнении и от деформативных свойств грунта основания.

Рис . 5 . Узел сопряжения связевых многопустотных (а) и ребристых плит (б) с ригелем

В монолитных плитных фундаментах сопряжение сплошной колонны с фундаментом рекомендуется принимать в виде жесткого защемления в уровне верха фундамента [35].

2.4.2 . Работу со пряжения колонны со столбчатым фундаментом необходимо рассматривать с учетом взаимодействия фундамента с грунтом. Податливость в основном вызывается деформациями грунта под подошвой фундамента.

2.5. Стыки сборных элементов перекрытия

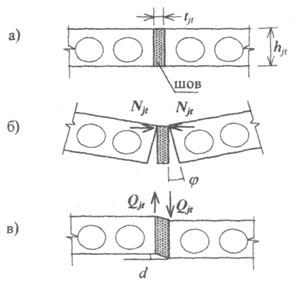
2.5.1 . Диски перекрытий из сборных железобетонных плит — многопустотных, ребристых, сплошных и т.п., уложенных по сборным ригелям без армированных набетонок, объединенных бетонными швами (рис. 6 ) или дискр етными сварными соединениями (рис. 7 ) в своей плоскости податливы за счет повышенной деформативности соединений на опорах и межплитных швов.

2 .5.2. В сборных перекрытиях имеются следующие типы стыков:

— вертикальные стыки торцов плит через бетонные швы с плитами или с опорными конструкциями (см. рис 5, а);

— продольные стыки между плитами и крайних плит со стенами (см. рис. 5, б и 5, в);

— горизонтальные стыки плит по опорным площадкам с поддерживающими конструкциями (стенами, балками или ригелями рис. 5, а и 5, в).

2.5.3 . Совместная работа многопустотных плит обеспечивается замоноличенными швами и сварными соединениями (для связевых и пристенных плит). Для увеличения сцепления бетона швов с конструкциями на их боковой поверхности устраиваются углубления для образования шпонок (рис. 8 ).

Рис . 6. Фрагмент плана сборного перекрытия из многопустотных п лит

Рис. 7 . Фрагмен т плана сборного перекрытия из плит 2Т

Рис. 8 . Типы боковой поверхности пустотных плит образующих после омоноличивания следующие формы межплитных шпонок:

а — замкнутые круглые; б — трапецевидные, открытые к верху; в — сплошные продольные

2 .5.4. В продольных швах различают шпонки трех типов:

— шпонки замкнутые круглые (рис. 8, а) работают на срез и обеспечивают совместную работу плит при вертикальных и горизонтальных нагрузках до стадии разрушения. Многократное приложение неравномерной вертикальной нагрузки до нормативного значения практически не снижает прочность межплитных продольных швов;

— шпонки открытые к верху в вертикальном направлении (прямые или трапециевидные рис. 8, б), включаются в работу за счет сцепления раствора омоноличивания с бетоном плит и его обжатия. Такой вид шпонок обеспечивает совместную работу п лит при горизонтальных нагрузках на диск п ерекрытия. Совместная работа плит до стадии разрушения при вертикальных нагрузках обеспечивается после устройства цементно-песчаной набетонки толщиной не менее 4 см;

— сплошные продольные шпонки (рис. 8, в) обеспечивают совместную работу плит при вертикальных нагрузках. При возникновении горизонтальных сдвигающих усилий прочность соединения обеспечивается только за счет сцепления бетона шва с плитами.

2.5.5 . Взаимодействие рядовых многопустотных плит с поддерживающими конструкциями (ригели, балки и несущие стены) при горизонтальных нагрузках обеспечивается силами трения и сцеплением подстилающего растворного слоя по опорным площадкам (рис. 9 ).

Торцевые швы между плитами и поддерживающими конструкциями работают только на сжатие и сдвиг перпендикулярно пролету (рис. 9).

Рис. 9 . Схема взаимодействия многопустотной плиты с ригелем:

τ_SH — касательные напряжения в торцевом шве при сдвиге плиты вдоль ригеля; τ _sc — касательные напряжения по площадке опирания плиты на ригель при сдвиге и повороте плиты относительно ригеля; σ_В — сжимающие напряжения в торцевом шве

2 .5.6. Взаимодействие ребристых плит с ригелями и балками при горизонтальных нагрузках обеспечивается сварными соединениями опорных закладных деталей (рис. 10 ). Совместная работа плит при вертикальных нагрузках обеспечивается продольными бетонными швами, выполняемыми, как правило, со шпонками.

Рис . 10. Схема взаимодействия ребристой плиты с ригелем:

τ_SH — касательные напряжения в торцевом шве при сдвиге плиты вдоль ригеля; Q _{z i} и N_Zi — усилия в сварном соединении плиты с ригелем; σ _в — сжимающие напряжения в торцевом шве

2.6. Соединения в сквозных связевых панелях

2. 6.1. Плоские сквозные связевые панели состоят из железобетонной многоэтажной рамы, образованной колоннами и ригелями и металлических связей треугольного (полураскосные) или пятиугольного (портальные) очертания (рис. 11 ).

Размещаются связевые конструкции из условия обеспечения пространственной жесткости здания, с учетом ограничения усилий от температурных деформаций.

2 .7.2. Фундаменты под связевые панели выполняются в виде отдельно стоящих столбчатых фундаментов, сплошной железобетонной плиты или железобетонной рамы. Конструкция фундамента зависит от размеров сетки колонн, величин действующих нагрузок и характеристик грунта.

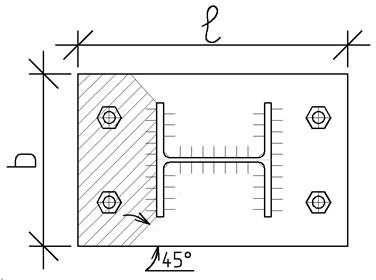
2.7.3 . Соединени я элементов связей между собой осуществляется с помощью приварки фасонок, что создает защемление по концам связей. Соединения связей с колоннами осуществляется в виде приварки связей через фасонки к закладным деталям на боковых гранях колонн (рис. 12 , а) или через фасонки, приваренные в тавр к внутренним закладным деталям.

Соединения связей с фундаментом чаще всего выполняются через фасонки, приваренные в тавр к закладным деталям фундамента (рис. 12, б).

Указанные соединения обладают линейной и угловой податливостью, вследствие повышенной деформативности закладных деталей при действии нормальных и поперечных сил, изгибающих, а также крутящих моментов в их плоскости.

Рис. 11 . Сквозные связевые панели с треугольной (а) и портальной (б) металлической решеткой

Рис . 12. Конструкция сопряжений металлических связей с колоннами (а) и фундаментом (б)

3. ПРАКТИЧЕСКИЙ МЕТОД ОЦЕНКИ ПОДАТЛИВОСТИ СОПРЯЖЕНИЙ

3.1. Вертикальные стыки колонн

3.1 .1. Податливость вертикального стыка колонн определяется как сумма податливостей на участках стыка с одинаковыми деформативными характеристиками по формуле

где п и l_i — количество и длина участков стыка с одинаковыми деформативными свойствами по длине; υ — коэффициент упруго пластических деформаций бетона; E _Bi — начальный модуль упругости бетона; А _Bi и A _Si — площадь бетона и продольной арматуры; α — коэффициент приведения, равный отношению модулей упругости арматуры и бетона.

Характер зависимости « N — δ» для типового вертикального стыка показан на рис. 13. По данным [4, 35] усредненный коэффициент линейной жесткости стыков для колонн сечением 40 ´ 40 см составляет С _Z = 7 ´ 10 6 кН/м.

Рис . 13. Диаграмма сжатия вертикального стыка колонн

3.2. Сопряжения ригеля с колонной

3.2 .1. В общем случае в сечении стыка ригеля с колонной действуют продольная и поперечная (относительно ригеля) силы, изгибающий и крутящий момент (рис. 14 ). В рассматриваемых конструкциях стыков ригеля с колонной вертикальная опорная реакция передается на консоль, поэтому влияние поперечных сил на работу сопряжения можно не учитывать.

Рис. 14. Схема усилий, действующих в узле сопряжения ригеля с колонной

3.2 .2. Работа сопряжения ригеля с колонной рассматривается для двух состояний: первое — швы не омоноличены, что соответствует стадии монтажа или конструкции так называемого сухого стыка (рис. 15 , а); второе — швы омоноличены и бетон шва включается в работу (рис. 15 , б, в).

3 .2.3. В стыках, по аналогии с сечениями железобетонных элементов, могут возникать три стадии напряженно-деформированного состояния: первая — у словно-упругая; вторая — упруго-пластическая и третья — предельная по несущей способности.

Рис . 15. Схема изменения напряженно-деформированного состояния сопряжения ригеля с колонной рамного каркаса:

а) стадия монтажа (сухой стык); б) омоноличенный узел до образования трещин в растянутой зоне; в) стадия после образования нормальной трещины в шве

3 .2.4. Критерием предельного состояния узлового сопряжения колонны с перекрытием рекомендуется принимать допустимый угол поворота опорного сечения ригеля или плиты перекрытия относительно оси колонны, который определяется:

— для первой группы предельных состояний из условий достижения физического или условного предела текучести в растянутой или сжатой арматуре, временного сопротивления сжатию бетона шва или стыкуемых конструкций, предельного сдвига или отрыва закладных деталей (рис. 16);

Рис. 16. Схема к определению предельного угла поворота ригеля относительно колонны:

Δ _s — предельные удлинения по растянутой арматуре; Δ _z — предельные деформации сдвига закладных деталей

— для второй группы предельных состояний из условий предельных прогибов и горизонтальных перемещений, так же предельного раскрытия трещин.

3.2 .5. Коэффициент угловой жесткости узла сопряжения ригеля (плиты перекрытия) с колонной С_φ равен отношению изгибающего момента М в узле к соответствующему углу поворота φ опорного сечения ригеля относительно оси колонны в узле:

3.2.6 . Угол поворота опорного сечения ригеля, показанного на рис. 16 определится

где Δ _Т = Σ Δ _{Т i} и Δ _С = -Σ Δ _{С i} — перемещения в растянутой и сжатой зонах (принимаются со своими знаками); Z _red — расстояние между линиями измерения перемещений.

3.2 .7. Для рассматриваемых типовых узлов сопряжения ригеля с колонной коэффициент угловой жесткости стыка рекомендуется определять по формуле

где 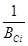и — приращения смещении от единичных усилий соответственно в сжатой и растянутой зонах сечения стыка; K _Ni , K _Nj — коэффициенты, учитывающие влияние осевого сжимающего усилия (при отсутствии продольной силы принимаются равной единице); h ₀ — рабочая высота сечения стыка (расстояние от линия опирания ригеля или плиты перекрытия на консоль до центра тяжести растянутой или сжатой арматуры).

3 .2.8. Коэффициент угловой жесткости сопряжения ригеля с колонной связевого каркаса (рис. 3 , а) без учета сжатого бетона шва:

где 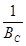, и — смещения от единичных усилий соответственно верхней стальной накладки, опорных закладных деталей консоли колонны и ригеля, определяемые по рекомендациям [27] или на основе экспериментальных данных;

(верхние знаки принимаются при совпадении усилий от изгибающего момента и продольной силы в нижней зоне); е — эксцентриситет продольной силы относительно линии опирания ригеля на консоль.

При действии обратного момента необходимо учитывать возможность потери устойчивости верхней связи.

3 .2.9. При действии момента противоположного знака в омоноличенных торцевых швах для узлового сопряжения ригеля с колонной связевого каркаса без верхней накладки, показанного на рис. 3 , б коэффициент угловой жесткости равен:

где ; d , E _B , ξ, v , ω — толщина шва, модуль упругости бетона шва, относительная высота сжатой зоны бетона шва, коэффициент упруго-пластических деформаций, коэффициент полноты эпюры сжатой зоны; K_{BN 1} , К _{BN 2} — коэффициенты, учитывающие влияние продольной силы

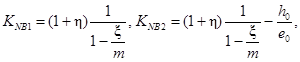
здесь m — коэффициент, зависящий от формы эпюры напряжений в бетоне сжатой зоны (3 — для треугольной, 2 — для прямоугольной).

Высота сжатой зоны определяется из условия равновесия сечения.

3.2.9 . Коэффициент угловой жесткости рамного сопряжения в монтажной стадии, т.е. без учета работы бетона шва на сжатие (рис. 15 , а):

где ;

здесь f(x) и l _jt — функция распределений продольных деформаций в растянутой арматуре (принимается по форме эпюры моментов на опорном участке) и длина учитываемой зоны растяжения верхней арматуры.

На участке с открытой растянутой арматуры стыка продольные деформации постоянны, поэтому 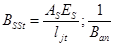— перемещения от единичных усилий растянутой арматуры в зоне анкеровки в бетоне, определяемые по рекомендациям [40].

3.2 .10. Выражение для коэффициента угловой жесткости при обратном моменте будет иметь вид:

В выражениях (7 и 8) при определении коэффициентов K _{N 1} и K_{n 2} необходимо учитывать правило знаков, описанное для выражения (5).

3.2 .11. Коэффициент угловой жесткости сопряжения рамного узла с учетом работы бетона шва на сжатие и образования нормальных трещин в бетоне шва растянутой зоны (рис. 15 , в):

где

3.3. Сопряжения в сборных дисках перекрытий

3 .3.1. Жесткость бетонного межплитного шва на изгиб принимается равной нулю, то есть шов рассматривается как цилиндрический шарнир. Однако сжимающая шов сила прикладывается не по оси боковой грани плит (рис. 17 ) и возникает внецентренное сжатие. Поэтому цилиндрический шарнир следует располагать по оси действия сжимающего усилия или в уровне сжатой грани плиты.

Рис. 17. Продольный межплитный шов (а), схема работы при повороте плит вдоль продольной оси (б) и сдвиге плит (в)

3.3.2 . Жесткость межплитного шва на сдвиг равна соответствующему усилию, вызывающему единичные перемещения:

Для участка шва, толщиной t _jt , высотой h _jt и длиной вдоль оси плиты l_jt получим:

где v = 1,2 — коэффициент, учитывающий неравномерность касательных напряжений по площади поперечного сечения элемента.

Влияние сдвиговой жесткости шва на совместную работу плит следует учитывать при значениях C _sh = 300 к Н/ м, что существенно меньше реальной жесткости. Для швов между типовыми многопустотными плитами значение сдвиговой жесткости на 1 м шва составляет: C _sh = 3080 · 10 4 кН/м [38].

3 .3.3. Растягивающие усилия в плоскости диска перекрытия из многопустотных плит воспринимаются в одном направлении связевыми межколонными плитами, в другом — ригелями.

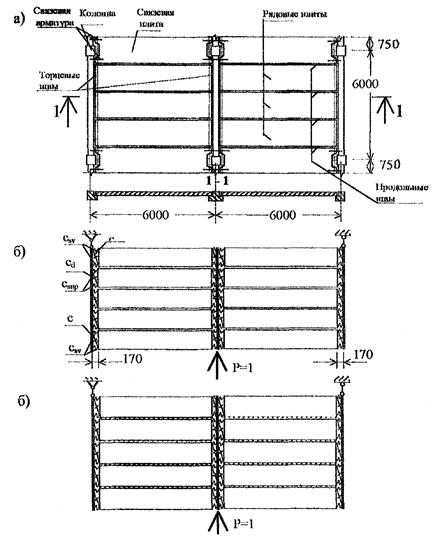
Линейная податливость связевых плит определяется согласно схеме рис. 18 по формуле:

Рис . 18. Расчетная схема к определению жесткости связевой плиты при растяжении в плоскости диска перекрытия:

1 — плиты; 2 — ригели; 3 — колонны; 4 — арматурные связи

3.3.4 . Жесткость на растяжение по зоне опирания связевой многопустотной или сплошной плиты на ригель (балку) определится по зависимости

где N _s = A _s · σ _s — усилие в связевой арматуре; N_sup = A _sUP · σ _sUP · f_tr — усилие для преодоления трения по площадкам опирания плит на поддерживающие конструкции:

здесь A _sUP и σ _sUP — площадь опирания и опорное давление плиты на ригель; f_tr — коэффициент трения плиты об опорную конструкцию; — деформации связевой арматуры; Δ _Z — деформации закладной детали, определяемые по рекомендациям [27].

Жесткость трения пустотной плиты рекомендуется определять при деформациях сдвига равных ε _sd = 100 ´ 10 5 . По данным [4, 14] значение податливости трения многопустотной плиты о ригель изменяется в пределах 1/C_tr = (0,3 ÷ 6) ´ 10 -6 м 2 /кН.

3 .3.5. В перекрытиях из ребристых плит при воздействии горизонтальной нагрузки на перекрытие опорное соединение воспринимает сдвигающее усилие, изгиб и кручение в своей плоскости (рис. 19 ). Суммарные линейные перемещения в сопряжении в общем случае складываются из деформации бетона опорной конструкции (Δ _В ), закладных деталей ригеля (Δ _XR ) и ребра (Δ _ХР ) плиты соответственно и деформаций (Δ _SV ) соединения по сварному шву

3 .3.6. Опорное сопряжение ребристой плиты с ригелем рекомендуется представить в виде стержня, сечение и длина которого определяется из условия равенства линейных и угловых деформаций.

Жесткость элемента связи при растяжении — сжатии в этом случае запишется

где N _x — горизонтальное усилие на соединение вдоль оси X .

Перемещения закладных деталей определяются по рекомендациям [27, 40]. Согласно экспериментальным данным жесткость типовых закладных деталей при действии сдвигающих сил, изменяется в пределах — (1 ÷ 12) ´ 10 4 кН/м.

Рис. 19. Фрагмент соединения ребристой плиты с ригелем (а) и расчетная схема соединения (б)

3 .3.7. При омоноличенных швах жесткость сопряжения ребра плиты с полкой ригеля (см. рис. 10 ) при сжимающих бетонный шов напряжениях составит:

где Е _в , A _Bred и а _в — модуль упругости бетона, площадь и толщина шва замоноличивания соответственно.

При действии горизонтальной силы, растягивающей бетонный шов, жесткость соединения определяется по зависимости (15).

3.3 .8. Жесткость соединения при изгибе опорной связи в своей плоскости определится из соотношения действующего изгибающего момента (М _Z ) и суммарных угловых деформаций в зоне опирания (рис. 19 ) по формуле

где M _z — крутящий момент, действующий в плоскости перекрытия, в месте опирания плиты на ригель в горизонтальной плоскости при повороте плиты относительно ригеля; φ _R и φ _P — углы поворота закладных деталей ригеля и ребра плиты; φ _{S v} — угол поворота вследствие деформаций сварного шва.

Например для закладных деталей, показанных на рис. 20 величина коэффициента угловой жесткости на начальной стадии изменяется в пределах С_φ = (2,5 — 6) ´ 10 4 кНм. При появлении неупругих деформаций коэффициент угловой жесткости снизился более чем в два раза и диапазон изменения составил С_φ = (1,1 — 2) ´ 10 4 кНм.

Рис. 20 . Схема испытания закладной детали (а) и опытные зависимости смещения закладных деталей от сдвигающей силы (б) данным испытаний [11]

3.3.9 . Высота и ширина сечения связи X и Y при фиксированной длине L определяется из условия равенства линейных и угловых деформаций из системы уравнений

3.3 .10. Размеры сечения стержневого элемента, воспринимающих растяжение или сжатие, для стыков без омоноличивания швов между торцом ребра и гребнем ригеля, определятся по формулам

3 .3.11. Для стержней, воспринимающих сжимающие усилия и поворот при омоноличенных торцевых швах параметры сечения определяются из системы уравнений ( 20 ) с учетом изменения коэффициента угловой жесткости за счет возникающего сопротивления повороту торцевого шва. Принимая, что центр поворота на опоре смещается незначительно коэффициент угловой жесткости при омоноличенных швах определится по формуле

где b _r — ширина ребра плиты.

Размеры сечения связи с учетом выражений (19) и (20) определятся по формулам

3.3 .12. В соединениях ребристых плит между собой с помощью приварки накладок к закладным деталям (рис. 21 , а) возникают продольное (по отношению к пролету плиты) усилие и изгибающий момент. Смещение плит в своей плоскости относительно друг друга будет складываться из деформаций сдвига закладной детали и ее поворота

где Δ _zp — смещения закладной детали вдоль кромок плиты; φ _{zs v} — угол поворота закладной детали; b _z — расстояние между закладными деталям плит.

Подставляя значения составляющих перемещений получим выражение для взаимного смещения плит в виде

где Q — сдвигающее усилие между плитами, приходящееся на одну закладную деталь; C _Zp , C _{φ z} — коэффициенты линейной и угловой жесткости закладной детали.

Рис. 21. Фрагмент соединения плит по продольному шву с помощью приварки накладок к закладным деталям (а) и расчетная схема соединения (б)

3.3.13 . Изгибная жесткость связевых элементов между плитами определится согласно схеме стержня с упруго податливыми защемлениями по формуле

где Е — модуль упругости стальной накладки.

3.4. Податливость сопряжений в связевых панелях.

3.4 .1. Податливость сопряжений металлических связей с железобетонной колонной при определении осевой жесткости связи рекомендуется учитывать по зависимости

где C _z — коэффициент линейной жесткости крепления элемента решетки к железобетонной раме при отрывающем усилии; Е, F и l — соответственно модуль упругости, площадь сечения и длина металлической связи.

3 .4.2. Жесткость сопряжения подкоса к фундаменту или к колонне через закладную деталь зависит от угла наклона отрывающего усилия и конструкции закладной детали (см. рис. 12 , б). Для портальных связей коэффициент жесткости составил в среднем С = 1,42 ´ 10 6 кН/м, для треугольной связи — С = 1,9 ´ 10 6 кН/м.

3 .4.3. Жесткость защемления при угловых деформациях для связей с боковыми накладками (см. рис. 12 , а) существенно выше изгибной жесткости связей для сетки колонн 6 м и более. На основании этого в расчетной схеме связевой панели узлы сопряжения металлической решетки с железобетонными колоннами рекомендуется принимать жестко защемленными от поворота.

Коэффициент угловой жесткости, согласно опытным данным в условно-упругой стадии деформирования изменялся в пределах С = (0,05 ÷ 0,36) ´ 10 6 кНм/рад, в упруго пластической — С = (0,05 ÷ 0,08) ´ 10 6 кНм/рад.

4. ФОРМИРОВАНИЕ РАСЧЕТНЫХ МОДЕЛЕЙ НЕСУЩЕЙ СИСТЕМЫ КАРКАСА ЗДАНИЯ

4.1. Общие положения

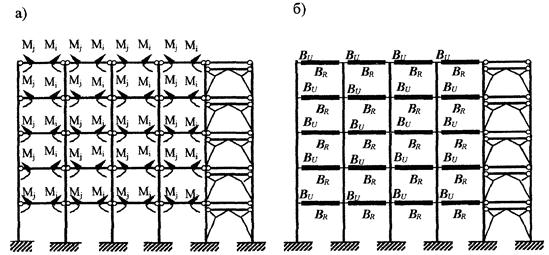
4 .1.1. Пространственную несущую систему каркаса рекомендуется разделять на плоские несущие подсистемы — продольные и поперечные рамы, диафрагмы жесткости и диски перекрытий (рис. 22 , а).

4 .1.2. По способу восприятия горизонтальных нагрузок каркасы классифицируются на рамные, связевые и комбинированные. Пространственная жесткость рамного каркаса (рис . 22 , б) обеспечивается жесткими (рамными) узлами сопряжения колонн (стоек) и перекрытий. В связевом каркасе (рис. 22 , в) сопряжения колонн и перекрытий принимается шарнирным, а пространственная жесткость обеспечивается вертикальными устоями — связевыми панелями, диафрагмами и ядрами жесткости. В комбинированных каркасах в одном направлении жесткость обеспечивается вертикальными устоями, в другом — жестким соединением колонн с ригелями, т.е. имеет место, как рамные, так и шарнирные сопряжения колонн с перекрытиями.

Рис. 22 . Схема пространственного каркаса (а) и плоские поперечные расчетные схемы для рамного (б) и связевого (в) каркасов

4.2. Методы учета податливости узловых сопряжений

4.2.1 . Расчет упругих статически неопределимых конструкций производится либо методом сил, либо методом перемещений. Для конструкций с малой статической неопределимостью рекомендуется к использованию метод сил. Метод перемещений имеет преимущества при в решениях систем с большой статической неопределимостью, но с малым количеством узловых точек.

4.2.2 . В методе сил в общем случае учет податливости узлов производится путем суммирования перемещений, вызванных деформациями стержней и податливостью соединений. При формировании основной системы отбрасываются лишние связи в податливых узлах, ограничивающие линейные или угловые деформации, в зависимости от искомого параметра.

Рис. 23 . Расчетная схема стержня с жестко защемленными концами (а) и расчетная схема стержня с упруго-податливыми при повороте опорами (б)

В системе канонических уравнений перемещения в отброшенных связях не обнуляются, а принимаются равными произведению податливости защемления на опорную реакцию [4]. Для простейшей статически неопределимой конструкции, показанной на рис. 23, система канонических уравнений с учетом податливости опор при повороте будет иметь вид:

где δ ₁₁ , δ₁₂ и δ₂₂ — перемещения от единичных усилий; X ₁ и X ₂ — реакции в отброшенных связях с учетом податливости сопряжений, равные:

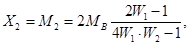
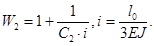
4.2.3 . Расчет конструкций с податливыми узлами методом перемещений производится таким же образом, как и с жестким или шарнирными узлами. Податливость узлов и опор учитывается при вычислении опорных реакций наложенных связей, которые можно определить, например, из системы уравнений ( 25 ). Таблицы с формулами по вычислению реакций в наложенных связях от единичных линейных или угловых перемещений упруго податливых опор представлены в работе [ 4 ].

4.2.4 . Для учета податливости сопряжений в расчетной схеме МКЭ реальные швы между сборными конструкциями следует представлять в виде податливых к.э., геометрические и жесткостные параметры которых максимально отвечают характеристикам реальных швов при различных стадиях возведения и нагружения несущей системы здания (рис. 22 ).

В качестве таких элементов можно использовать типовые стержневые и плоские к.э ., а также специальные элементы, имеющиеся в применяемой прикладной программе.

4 .2.5. Геометрические размеры к.э. сопряжений следует, по возможности, назначать равными размерам реальных швов, а механические характеристики задавать таким образом, чтобы их угловые и линейные перемещения от соответствующих единичных нагрузок были равны податливостям реальных швов.

4.2.6 . Для стыков колонн между собой длина элементов может быть принята равной конструктивной длине сопряжений l_fe = l_jt. Поскольку к.э. сопряжений обычно более податливы, чем примыкающие элементы, здесь и далее, для наглядности, они изображены в виде пружин (рис. 24 , а).

4 .2.7. Для стыков ригелей с колоннами (рис. 24 , б), а также железобетонных элементов сборных диафрагм, чтобы сохранить геометрию системы необходимо вводить жесткие элементы (вставки) длиной, равной

Длина зоны стыка, имеющая повышенную деформативность, может быть разной в зависимости от его конструктивного решения. Как показали расчеты, длина конечного элемента, моделирующего податливый стык, не должна быть более 1/6Н, где Н — высота сечения ригеля.

Рис. 24 . Расчетная схема сопряжений сборных железобетонных элементов для расчета по МКЭ:

а) стыки колонны; б) сопряжение ригеля с колонной

4.2.8 . Характеристики податливости к.э. в узловых сопряжениях рекомендуется принимать из условия

где С_{φ fe} и С_{φ jt} — коэффициенты жесткости для заменяющего конечного элемента и шва (сопряжения ригеля с колонной).

4.2.8 . Учитывая, что сдвиговые деформации в стержневых элементах вообще, а особенно на коротких участках шва, практически не влияют на перемещения конструкции при назначении деформационных характеристик к.э. швов достаточно задание трех независимых величин. Это характеристики податливости шва при действии моментов в двух плоскостях и при действии нормальной силы.

4.2 .9. Если в качестве к.э. швов используются специальные стержневые элементы, то их деформационные характеристики задаются, чаще всего, непосредственно, как величины, характеризующие перемещения от единичного усилия (податливость) или усилия от единичного перемещения (жесткость). При применении стандартных стержневых к.э., их следует принимать прямоугольного сечения. В этом случае при задании исходных данных используются три независимых параметра: высота ( h ) и ширина ( b ) сечения и модуль упругости ( E ), которых достаточно для описания требуемых характеристик швов. Указанные параметры можно определить, используя известные зависимости выражения осевой и изгибной жесткости для прямоугольного сечения через линейную и угловую податливость соответственно в виде

где 1/С_Δ, 1/ С _{φ y} , 1/ С_{φ x} — податливости стыков при действии на них, соответственно, нормальной силы, изгибающего момента в плоскости оси «х» и «у»; l_jt , b и h — толщина шва и размеры сечения конечного элемента вдоль осей «х» и «у».

Тогда искомые характеристики сечения определятся по формулам

Численные значения этих величин для каждого типа сопряжения следует принимать на основании экспериментальных данных или по выражениям гл. 2, рассматривая каждый узел как совокупность отдельных элементов. При этом рекомендуется принимать некоторые упрощения, основанные на анализе возможного напряженно-деформированного состояния каждой группы однотипных узлов и его влияния на работу несущей системы.

4 .2.10. Для сопряжений ригелей с колоннами основное влияние на работу несущей системы каркасного здания оказывает податливость узлов при действии изгибающих моментов в плоскости рамы. Деформативность же таких узлов при действии на них моментов из плоскости влияет на работу плоских рам в меньшей степени. Соответственно выражения ( 28 ) могут быть упрощены. Тогда при наличии экспериментальных данных по величинам соответствующих податливостей жесткость соединений может быть определена как для сплошного железобетонного сечения с приведенным значением модуля упругости. Это позволит при описании к.э. сопряжений с помощью стандартных элементов принимать их сечения такими же, как в ригелях, а приведенные значения модулей упругости назначать, исходя из значений податливости реальных швов при их изгибе в соответствующей плоскости по формуле

где I — момент инерции принятого сечения к.э. шва.

4.2 .11. В узловых сопряжениях сборных железобетонных элементов, в которых наибольшее влияние на напряженно-деформированное состояние оказывает деформативность при сдвиге и растяжении-сжатии в плоскости, а сопротивление каждого сопряжения моменту в этой плоскости и из плоскости практически близко к нулю, сопряжение рекомендуется моделировать стержнем, жестко защемленным одним концом с шарниром на другом. В стандартных программных комплексах предусмотрены специальные к.э., позволяющие независимо задавать жесткостные характеристики при растяжении-сжатии и сдвиге.

4.3. Многоэтажные рамы каркаса

4.3 .1. Плоская расчетная схема многоэтажных связевых каркасов представляет комбинированную конструкцию, состоящую из рамной части и связевого элемента — диафрагмы жесткости (рис. 22 , в). В расчетной схеме узлы сопряжения ригелей и плит с колоннами при расчете на вертикальную нагрузку во многих конструктивных решениях рекомендуется принимать шарнирными. При действии горизонтальной нагрузки, в результате конструктивных факторов, описанных в разделе 2 , возникает частичное защемление, которое ограничивает поворот колонн относительно элементов сборного перекрытия в продольном и поперечном направлениях. Появление сопротивления взаимному повороту элементов в узлах сопряжения повышает жесткость продольных и поперечных рам, тем самым разгружая связи и диафрагмы жесткости.

4.3 .2. Характеристикой частичного защемления принята величина податливости сопряжения (обратная величина коэффициента угловой жесткости). Изменения податливости узла сопряжения ригеля с колонной связевого каркаса вследствие проявления нелинейности незначительна и в практических расчетах можно принимать коэффициент угловой жесткости сопряжения постоянным.

Рис . 25. Расчетные схемы рам связевого каркаса с учетом частичного защемления колонн в перекрытии:

а — введение дополнительных опорных моментов в шарнирные узлы сопряжения ригеля с колонной; б — введение в расчетную схему участка ригеля с пониженной жесткостью

4.3.3 . Усилия в элементах рамных каркасов существенно изменяются за счет изменения соотношения жесткостей элементов рамы в процессе нагружения (эксплуатации). Жесткость рамного сопряжения в процессе увеличения изгибающего момента снижается за счет проявления неупругих деформаций в растянутой арматуре, в бетоне и закладных деталях сжатой зоны опорного сечения (см. п. 2 ). В связи с этим при расчете на вертикальные нагрузки следует учитывать переменную податливость сопряжения ригеля с колонной.

4.3 .4. Основная часть усилий в рамном сопряжении возникает от вертикальных нагрузок и в растянутой арматуре допускаются напряжения, соответствующие пределу текучести. Вследствие этого происходит накопление остаточных деформаций и при действии знакопеременных горизонтальных нагрузках имеет место большая деформативность сопряжения ригеля с колонной по сравнению с жестким защемлением. На основании этого при расчете на горизонтальные нагрузки податливость узловых сопряжений перекрытия с колонной следует определять по максимальным усилиям от вертикальных нагрузок.

4.4. Учет нелинейности деформирования стержневых элементов

4.4.1 . Физическую нелинейность деформирования стержневых элементов в упругих методах расчета рекомендуется производить на основе итераций с одновременным изменением геометрии сечения за счет трещинообразования и снижения модуля деформаций бетона и арматуры в соответствии с их диаграммами деформирования, включая нисходящие участки.

4 .4.2. Конструктивную нелинейность деформирования узловых сопряжений рекомендуется учитывать установкой односторонних связей или путем введения различной жесткости соединений в зависимости от направления деформирования.

4.4 .3. При расчете рам методом конечных элементов учет нелинейности деформирования целесообразно производить с помощью переменного модуля упругости при постоянной геометрии сечений на основе диаграммам «М — 1/ρ». При таком подходе модуль упругости приобретает комплексный смысл. Характер изменения приведенного модуля упругости должен основываться на реальных свойствах материалов и конструктивных особенностях элемента или сопряжения.

4.4.4 . Для учета изменения коэффициента угловой жесткости сопряжения ригеля с колонной можно с достаточной точностью можно принять его линейную зависимость от угловой деформацией в виде:

где С_{φ 0} — начальный коэффициент жесткости стыка; С_{φ R} и φ _R — коэффициент жесткости стыка и угол поворота соединения в стадии предельной по несущей способности.

4.4 .5. Точное определение изгибной жесткости стержневых железобетонных элементов основано на распределении продольных деформаций элемента по гипотезе плоских сечений и определении напряжений с использованием аппроксимирующих диаграмм арматуры и бетона. В железобетонном изгибаемом элементе неравномерность деформаций вдоль элемента при изгибе учитывается коэффициентами ψ _s и ψ_В соответственно для арматуры и бетона.

4.5. Диск перекрытия из сборных элементов

4 .5.1. Расчетные схемы сборных балочных дисков перекрытий для расчета на горизонтальные нагрузки, фрагменты которого показаны на рис. 6 , 7 , зависят в основном от таких факторов, как тип плиты перекрытия, конструкции продольных швов и условий опирания [ 15 , 16 , 17 , 19 , 29 — 31 ].

4.5.2 . Концентрация деформаций происходит в зонах сопряжений сборных конструкций, на основании этого расчетную модель ячейки перекрытия рекомендуется представлять в виде (рис. 26 ) плоскостных (1) и стержневых (2) элементов, соединенных деформируемыми связями (3). Учет работы перекрытия из своей плоскости производится путем использования в расчетной модели пластин и связей как пространственных элементов.

4 .5.3. Плоскостные элементы (1) моделируют работу плиты в горизонтальной плоскости и в расчетной модели представляются конечными элементами типа «плита» или «оболочка». Жесткость пластины в своей плоскости по сравнению с жесткостью связей во много раз выше. Основными параметрами для элементов (1) являются геометрия в плане и назначение приведенной толщины для учета работы пластины на изгиб и кручение.

Рис. 26 . Расчетная модель ячейки перекрытия (а) и схемы ее формирования в своей плоскости при отсутствии (б) и наличии (в) заполнения продольных швов

4.5 .4. Жесткостные характеристики связей (3) зависят от направления деформирования, которое можно установить на основе анализа кинематической схемы перемещений сборных элементов диска. В общем случае могут быть две граничные схемы: первая схема (рис. 26 , б) возникает при отсутствии заполнения продольных швов, тогда горизонтальные нагрузки приводят к независимому параллельному повороту и смещению плит; вторая схема (рис. 26 , в) — при полном омоноличивании швов и ячейка перекрытия или объединенные швом плиты перемещаются как единая пластина. Рекомендации к определению податливости связей даны в главе 2.

4.5 .5. В составе диска перекрытия температурного блока здания условия работы ячейки перекрытия будут зависеть от размеров сетки колонн и расположения ее в плане здания: ячейка крайнего ряда колонн; ячейка среднего ряда; ячейка примыкающая непосредственно к диафрагме жесткости или лестничной шахте. Это в свою очередь определяет количество наложенных связей между ячейками.

4 .5.6. При использовании в качестве расчетных моделей сборных дисков перекрытий сплошных однородных пластин, учет податливости сопряжений рекомендуется производить понижением модуля упругости материала перекрытий на величину коэффициента К_Е, который определяется по выражению

где f_G и f_P — прогибы перекрытия в горизонтальной плоскости по модели как сплошной пластины и по пластинчато-стержневой модели соответственно.

5. ПРИМЕРЫ РАСЧЕТА

В настоящем разделе приведены примеры определения податливости стыков типовых железобетонных конструкций часто встречающихся в практике проектирования. Даны примеры расчета плоской поперечной рамы связевого каркаса и фрагмента диска перекрытия из многопустотных плит на действие единичных горизонтальных нагрузок. Характеристики податливости закладных деталей приняты по экспериментальным данным НИИЖБ и ОАО ЦНИИПромзданий.

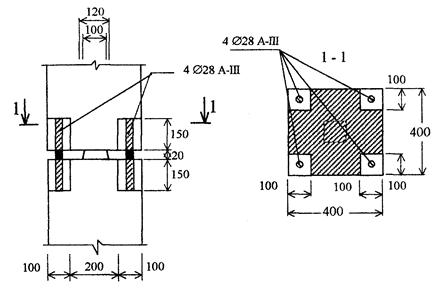
Пример 1 . Определить линейную податливость вертикального стыка колонн, показанного на рис. 27 . Исходные данные: сечение колонн 40 ´ 40 см; бетон тяжелый класса В20 с начальным модулем деформаций Е _b = 24000 МПа; продольная арматура из стали класса AIII 4 Æ 28 — A _s = 24,63 см 2 , E _s = 200000 M П a ; коэффициент v = 0,45.

Коэффициент приведения равен

Податливость стыка равна

Рис. 27 . Пример вертикального стыка колонны

Пример 2 . Определить коэффициент угловой жесткости узла сопряжения ригеля с колонной связевого каркаса с верхней накладкой, показанного на рис. 3 , а. Исходные данные: площадь сечения накладки A_n = 6 см 2 ; модуль упругости Е _N = 2,1 ´ 10 4 кН/см 2 , жесткость опорной закладной детали при сдвиге G_Z = 2,5 ´ 10 3 кН/см, рабочая высота сечения стыка h ₀ = 27 см. Продольное усилие в ригеле от горизонтальной ветровой нагрузки N = 23 кН .

Предельный изгибающий момент, воспринимаемый сечением стыка

Коэффициент угловой жесткости сопряжения

Коэффициент угловой жесткости неомоноличенного сопряжения при действии обратного момента определим с учетом продольного изгиба верхней пластины. При гибкости пластины

коэффициент угловой жесткости сопряжения

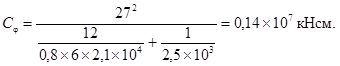
Влияние продольной силы на жесткость сопряжения определим в предположении, что сила действует в уровне опорной закладной детали (е = 0). Тогда

Коэффициент угловой жесткости сопряжения с учетом продольной силы

Пример 3 . Определить коэффициент угловой жесткости омоноличенного узла сопряжения ригеля с колонной связевого каркаса без верхней накладки, показанного на рис. 3 , б, при действии обратного момента. Исходные данные: рабочая высота, ширина и толщина сечения стыка h ₀ = 30 см, b = 30 см, d = 2 см; бетон шва класса В12,5 с модулем упругости Е _в = 2100 кН/см 2 , жесткость опорной закладной детали при сдвиге G _z = 2,5 ´ 10 3 кН/см.

Принимая эпюру сжатого бетона шва треугольной формы высота сжатой зоны определиться на основе гипотезы плоских сечений по выражению

Коэффициент угловой жесткости сопряжения

Пример 4 . Определить коэффициент угловой жесткости рамного сопряжения ригеля с колонной, показанного на рис. 4 , б в начальной стадии и при действии расчетных нагрузок. Пролет ригеля принимается равным 6 м. Верхняя растянутая арматура выполнена из 3 Æ 36 АIII. Модуль упругости арматуры E _s = 2,1 ´ 10 5 M П a, A_s = 30,54 см 2 . Соединение осуществлено сваркой опорной закладной детали, ванной сваркой выпусков верхней арматуры и приварки дополнительных соединительных пластин по бокам консоли из листовой стали сечением 100 ´ 10 мм. Жесткость опорной закладной детали при сдвиге принимаем равной G _z = 2 ´ 10 5 кН/см.

Рассмотрим монтажную стадию при отсутствии бетона омоноличивания. В соответствии с рис. 4, б в сжатой зоне при вертикальных нагрузках сопротивление оказывает сварное соединение по опорной закладной детали и накладки из листовой стали, равные

где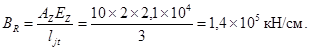

Выражение для изгибающего момента в опорном сечении относительно центра тяжести растянутой арматуры определиться по выражению

Приведенное значение плеча внутренней пары сил определим из условия

Коэффициент жесткости стыка в начальной стадии при расчетной свободной длине растянутой арматуры l _{j t , s} = 17 см равен

Коэффициент угловой жесткости стыка в стадии близкой к предельной определим по величине угла поворота опорного сечения соответствующего допустимому прогибу конструкции при равномерно распределенной нагрузке. При f = l /200 угол поворота опорного сечения составит φ = 0, 016.

Несущая способность узлового сопряжения равна

М = A _s R _s Z_red = 30,54 ´ 36,5 ´ 41,69 = 46472,26 кНсм.

Коэффициент угловой жесткости, соответствующий предельному повороту опорного сечения составит

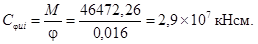
Деформативность рамного узла обеспечивается в основном растянутой арматурой, поскольку суммарные деформации закладных деталей в рассматриваемой конструкции узла, как показывают эксперименты, проведенные в ЦНИИПромзданий, невелики. При омоноличивании швов жесткость сжатой зоны увеличится, а их учет не существенно скажется на снижении коэффициента угловой жесткости.

Пример 5 . Определить на сколько увеличатся пролетные моменты в балке с податливым защемлением (см. рис. 23 ) по сравнению с балкой с жестко защемленными опорами. Исходные данные: ригель пролетом l = 6 м, из бетона класса В30, Е _в = 3250 кН/см 2 ; момент инерции сечения ригеля J = 294652,7 см 4 . Принимаем коэффициенты угловой жесткости из примера 4 С_М = 4,7 ´ 10 7 кНсм и С_{М l} = 2,9 ´ 10 7 кНсм .

Вычисляем параметры для системы уравнений (25)

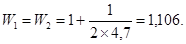
Изгибающий момент на опоре

Соотношение моментов составит

Таким образом снижение опорных моментов в упругой стадии составляет всего 7 %. При понижении коэффициента угловой жесткости стыков до значения С _M = 2,9 ´ 10 7 кНсм и изгибной жесткости за счет образования и раскрытия трещин снижение опорного момента может достигать 34 %.

Пример 6 . Определить, как изменятся прогибы трехэтажной двух пролетной рамы (рис. 28 , а) от горизонтальной нагрузки при учете возникновения одностороннего податливого защемления в узлах сопряжения ригеля с колонной. Величину коэффициента угловой жесткости принимаем равным С _м = 0,2 ´ 10 7 кН/см. Исходные данные: колонны сечением 40 ´ 40 из бетона класса В20 (Е _в = 2700 кН/см 2 ) армированные 4 Æ 22 AIII ( A _s = 15,2 см 2 ); ригели типовые высотой 45 см из бетона класса В25 (Е _в = 3000 кН/см 2 ), армированные преднапряженной арматурой 4 Æ 20 AIV ( E_s = 19000 к H/ см 2 ). Узловые сопряжения выполнены по рис. 3 , а.

Рис. 28 . Расчетная схема рамы (а), график прогибов от горизонтальной нагрузки (б) и поперечные сечения элементов рамы (в)

Расчет рамы производим методом конечных элементов с использованием программного комплекса Лира Windows. Учет продольной арматуры в сечениях элементов производим изменением модуля упругости бетона с помощью коэффициента

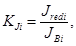
где J_redi и J_{b i} — моменты инерции сечений с учетом продольного армирования и только для бетонного сечения.

Определяем геометрические характеристики сечений элементов рамы (рис. 2.П, в):

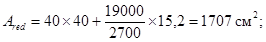
J_redK = 213333,3 + 7,03 ´ 2 ´ 7,6 ´ 17 2 = 244214,7 см 4 ;

K_JK = 244214,7/213333,3 = 1,14;

A _R = 30 ´ 30 + 53,5 ´ 22 = 1867 см 2 ;

A_redR = 1867 + 7,03 ´ (12,56 + 4,02) = 1983 см 2 ;

S_B = 30 ´ 23 ´ (22 + 11,5) + 53,5 ´ 22 ´ 11 = 36062 см 3 ;

S _redR = 36062 + 7,03 ´ (12,56 ´ 4,5 + 4,02 ´ 42) = 37645 ,9 см 3 ;

у _0R = 36062/1867 = 19,3 см; у _redR = 37645,9/1983 = 18,9 см;

J _redR = 227812,5 + 30 ´ 45 ´ (22,5 — 18,9) 2 + 20852,3 + 23,5 ´ 22 ´ (18,9 — 11) 2 + 7,03 ´ 4,02 ´ (43 — 18,9) 2 + 7,03 ´ 12,56 ´ (18,9 — 4,5) 2 = 333150 см 4 ;

Модули упругости колонны и ригеля составят

E _redK = 2700 ´ 1,14 = 3078 кН/см 2 ;

E _redR = 3000 ´ 1,117 = 3351 кН/см 2 .

Поскольку задача стоит в определении степени влияния частичного защемления на прогибы рамы расчет производим на единичные горизонтальные нагрузки.

Разбивку рамы на конечные элементы производим следующим образом: длина элементов ригеля принимается равной высоте т.е. l _r = 45 см ; длину элемента, моделирующего податливое защемление принимаем равным l _jt = 0,1 h = 4,5 см; длина конечных элементов колонны соответствует высоте этажа. Приведенный модуль упругости элемента сопряжения определиться по формуле (29)

Результаты распета представлены в виде графика на рис. 28, б, где линия (1) соответствует прогибам при всех шарнирных сопряжениях ригеля с колонной и линия (2) прогибам при учете частичного одностороннего защемления колонн в узлах сопряжения. Снижение прогибов от горизонтальной нагрузки составило 70 %. При этом изгибающие моменты в уровне защемления колонн в фундаментах снизились в два раза.

Пример 7 . Оценить жесткость фрагмента перекрытия из типовых многопустотных плит в своей плоскости при действии горизонтальной нагрузки. Фрагмент перекрытия, показанный на рис. 29 , а, состоит из двух ячеек по пять плит в каждой. Расстояние между колоннами составляет 6 м. Плиты опираются на железобетонные ригели. Ячейки объединены связевой арматурой Æ 18 АIII по крайним плитам распоркам. Плиты выполнены из бетона класса В20, характеристики ригелей взяты из примера 6 . Расчет производим методом конечных элементов с использованием программного комплекса Лира Windows.

Рис. 29 . Фрагмент сборного перекрытия из многопустотных плит (а), расчетная модель перекрытия при отсутствии бетона омоноличивания в швах (б) и при омоноличивании продольных швов (в)

Необходимо рассмотреть две схемы работы фрагмента перекрытия: без учета продольных межплитных швов т.е. на стадии монтажа и с учетом омоноличивания швов.

Принимаем, что ригели фрагмента перекрытия по краям опираются на не смещаемые в горизонтальной плоскости опоры. Горизонтальная единичная нагрузка действует по линии среднего ригеля (рис. 29, б).

Расчетная модель фрагмента перекрытия для монтажной стадии показана на рис. 29 , б на которой пластины моделируют сборные плиты перекрытия, стержневые элементы — ригели, податливые связи взаимодействие между плитами и ригелями. Взаимодействием между плитами вдоль продольных швов на стадии монтажа из-за малости пренебрегаем. Для того, чтобы исключить сдвиг плит вдоль направления ригелей вводим дополнительный диагональный элемент соединяющий плиту и ригель в торце каждой плиты (рис. 29 , б). Жесткость дополнительных стержней заведомо назначаем большой. Таким образом податливые связи работают практически только на растяжение-сжатие.

Длину податливых связей принимаем равной 17 см.

Погонная податливость по опорным площадкам за счет сил трения и сцепления принимаем по данным [2] равной 1/С _f = 5,56 ´ 10 2 см 2 /кН. Взаимодействие по опорным площадкам моделируем в виде 2х стержней (арматура класса А III ) площадь сечения которых с учетом ширины плиты 1,5 м равна

По плитам распоркам с учетом взаимодействия по опорным площадкам в расчетной модели принимаем диаметр стержней 2,2 см. Характеристики элементов модели представлены в таблице 1.

Источник