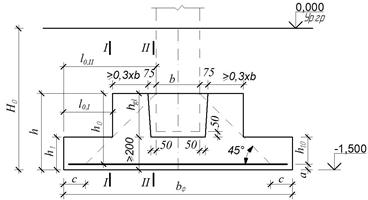
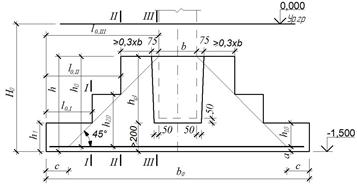
Подбор размеров подошвы и ступеней фундамента
Расчетное сопротивление грунта по II группе предельных состояний
Марка бетона В15; марка стали А240.
— Нормативная нагрузка на фундамент
Nп = 
N=1164,63 — из расчета колонны; γf,red = 1.15 – осредненный коэффициент надежности по нагрузкам.
— Требуемая площадь подошвы фундамента
;
ρ=20кН/м³; — осредненный объемный вес бетона и грунта; Н1=1,2м – глубина заложения фундамента.
.
— Размеры сторон подошвы фундамента
а = 
.
Принимаем а =2,4, тогда А= а²=5,76 м².
— Давление на грунт под подошвой фундамента
P= 
— Определяем рабочую высоту фундамента из условия продавливания
hо= 
— Высота фундамента из условия продавливания
а = aз.с. + 0,5ds = 40 + 0,5∙20 = 50 мм, aз.с=40 мм – толщина защитного слоя бетона в грунте, ds= 20 мм предварительный диаметр арматуры подошвы фундамента.
Минимальная высота фундамента по конструктивным требованиям:
— из условия заделки колонны в фундамент
t = 200мм, толщина дна стакана фундамента, δ = 50 мм – конструктивный зазор для выверки фундамента по высоте.
— из условия анкеровки арматуры колонн
Принимаем высоту фундамента Н кратно 300мм., тогда Н = 900мм.
Проверяем подошву фундамента расчетом по наклонным сечениям из условия, чтобы не требовалась установка поперечной арматуры
Задаемся: длина второй ступени а1= 1,8 м.; высота нижней ступени h1=0,3м.; рабочая высота нижней ступени; hо1= 0,3-0,05=0,25м.
где в =2,4м. ширина фундамента
121500 Н=121,5 кН
Принимаем по сортаменту: 13Ø12 Аs=1470 мм².
% =0,52%
Источник
Расчет и конструирование фундамента
В курсовом проекте в качестве фундаментов под колонны предлагается запроектировать центрально-нагруженные столбчатые фундаменты стаканного типа. Фундаменты предлагается запроектировать монолитные из бетона класса В15, в качестве основной несущей арматуры необходимо применять арматуру А300 или А400 в зависимости от указанной в задании.
Так как фундаменты центрально-нагруженные, то их обычно изготавливают семеричными (подошва имеет квадратную в плане форму).
Количество ступеней (см. рисунок 2.5.1) назначают в зависимости от высоты фундамента h: при 450мм о .
Рисунок 2.5.1 – Фундаменты стаканного типа а) двухступенчатый, б) трехступенчатый
Глубину заложения фундамента в курсовом проекте условно назначена 1500мм. Вообще глубина заложения для Новосибирска назначается обычно ниже глубины промерзания грунта, равного 2,2м, но так как в проекте необходимо запроектировать фундамент под среднею колонну, то его глубину заложения можно назначать меньше. Расчетное сопротивление грунта R0 – задано в задании.
Глубина стакана hgl принимается равной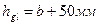 
, где b – размер сечения колонны. Толщина дна стакана принимается не менее 200мм во избежание ее продавливания в процессе монтажа колонны.
Минимальную площадь подошвы фундамента можно определить по формуле:
, /2.5.1/
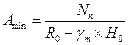
где Nn – нормативное значение усилия действующего от колонны на фундамент (приблизительно можно принять равным Nn=N/1,15) N – продольное усилие в колонне первого этажа;
– усредненный удельный вес фундамента и грунта на уступах фундамента равный 20кН/м 3 ;
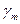
Н0 – глубина заложения фундамента (в курсовом проекте условно принято 1,5м).
Так как для центрально-нагруженных фундаментов предполагается квадратная подошва, тогда минимально допустимый размер фундамента bф можно определить как:
/2.5.2/
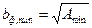
При этом размер подошвы фундамента назначают кратно 300мм. Площадь фундамента будет равняться
. /2.5.3/
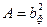
Минимальная высота всего фундамента под сборную колонну по конструктивным соображениям определяется как:
. /2.5.4/
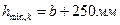
Минимальная высота фундамента из условия среза определяется как:
, /2.5.5/
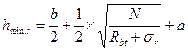
где N – расчетное усилие, действующее на фундамент от колонны;
— интенсивность давления грунта на подошву фундамента определяемая как 
;
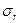
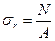
а – расстояние от грунта до равнодействующей в растянутой арматуре, принимается равной 30…60мм если выполняется подготовка под подошву фундамента и не менее 70мм в случае ее отсутствия.
Высоту фундамента h назначают как большую из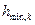 
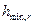
и 
при этом она должна быть кратна 150мм.
Рабочая высота нижней ступени фундамента h1,0 определяется из условия равновесия, где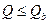 
, 
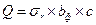
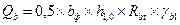
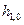
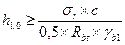
— внешнее усилие в наиболее опасном сечении, 
— минимальное усилие воспринимаемое бетонным сечением без поперечного армирования. Разрешив это неравенство относительно 
, получим, что минимальная рабочая высота первой ступени должна быть:
. /2.5.6/
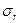
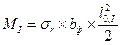
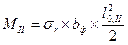
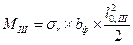
Для определения площади сечения арматуры в нормальных сечениях I-I, II-II, III-III определяют расчетные моменты в этих сечениях как для консольной балки, от интенсивность давления грунта на подошву фундамента . Величина этих моментов равняется:
/2.5.7/
/2.5.8/
/2.5.9/
Требуемая площадь сечения арматуры определяется по приближенной формуле:
— для любого фундамента /2.5.10/
— для трехступенчатого фундамента /2.5.11/
— для двухступенчатого фундамента /2.5.12/
— для трехступенчатого фундамента /2.5.13/
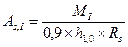
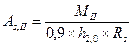
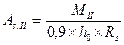
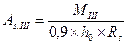
Так как внутренние момент возникающий в подошве фундаменте определялся на всю ширину фундамента, то и требуемая площадь арматуры определяется на всю ширину фундамента. Требуемую площадь сечения одного стержня можно определить по формуле:
, /2.5.14/
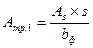
где s – шаг стержней в подошве фундамента, можно применять 100, 125, 150, 175 или 200мм.
По требуемому значению площади сечения одного стержня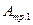 
определяется необходимый диаметр рабочих стержней при назначенном шаге. При этом в связи с тем, что фундамент центрально нагружен стержни в продольном и поперечном направлении одинаковы.
Источник
Определение высоты плитной части фундамента и размеров ступеней расчётом на продавливание
Черт. 6. Виды сопряжений фундамента с колонной по 1-й схеме расчета на продавливание
а — монолитное сопряжение колонны с плитной частью фундамента; б — то же при высоте подколонника hcf □ 0,5 (lcf — lc); в — стаканное сопряжение колонны с высоким фундаментом при hcf — dp □ 0,5 (lcf — lc)
Черт. 7. Сопряжение сборной колонны с низким фундаментом при hcf — dp □ 0,5 (lcf — lc)
2.7. При опирании на фундамент двух или более колонн, а также двухветвевых колонн продавливание рассматривается при воздействии на фундамент условной колонны, размеры которой равны габаритам по наружным граням колонн, а глубина стакана принимается в уровне наиболее заглубленной колонны (черт. 8).
Черт. 8. Схемы продавливания фундамента при опирании на него двух колонн
а — расположение колонн в одном уровне; б — расположение колонн в разных уровнях; 1 — внутренняя грань стакана; 2 — наружная грань условной колонны
Расчет на продавливание по схеме 1 (см. черт. 6)
2.8. Расчет на продавливание плитной части центрально-нагруженных квадратных железобетонных фундаментов производится из условия
F □ Rbt um h0,pl , (1)
где F — продавливающая сила;
Rbt — расчетное сопротивление бетона осевому растяжению, принимаемое с необходимыми коэффициентами условий работы □b2 и □b3 в соответствии с табл. 15 СНиП 2.03.01-84 как для железобетонных сечений;
um — среднеарифметическое значение периметров верхнего и нижнего оснований пирамиды, образующейся при продавливании в пределах рабочей высоты сечения h0,pl
um = 2 (bc + lc + 2 h0,pl) . (2)
При определении величин um и F предполагается, что продавливание происходит по боковой поверхности пирамиды, меньшим основанием которой служит площадь действия продавливающей силы (площадь сечения колонны или подколонника), а боковые грани наклонены под углом 45° к горизонтали (черт. 9).
Черт. 9. Схема образования пирамиды продавливания в центрально-нагруженных квадратных железобетонных фундаментах
В формуле (2) и последующих формулах раздела величины bc, lc заменяются размерами в плане сечения подколонника bcf, lcf, если продавливание происходит из нижнего обреза подколонника.
Величина продавливающей силы F принимается равной величине продольной силы N, действующей на пирамиду продавливания, за вычетом величины реактивного давления грунта, приложенного к большему основанию пирамиды продавливания (считая до плоскости расположения растянутой арматуры).
2.9. Расчет на продавливание центрально-нагруженных прямоугольных, внецентренно нагруженных квадратных и прямоугольных фундаментов (черт. 10) также производится в соответствии с п. 2.8 и условием (1). При этом рассматривается условие прочности на продавливание только одной наиболее нагруженной грани пирамиды продавливания.
Величина продавливающей силы F в формуле (1) принимается равной
где Ao — часть площади основания фундамента, ограниченная нижним основанием рассматриваемой грани пирамиды продавливания и продолжением в плане соответствующих ребер (многоугольник abcdeg, см. черт. 10).
Черт. 10. Схема образования пирамиды продавливания в центрально-нагруженных прямоугольных, а также
внецентренно нагруженных квадратных к прямоугольных фундаментах
Ао = 0,5b (l — lc — 2h0,pl) — 0,25 (b — bc — 2h0,pl)2 , (4)
при b — bc — 2h0,pl □ 0 (черт. 11) последний член в формуле (4) не учитывается;
Черт. 11. Схема образования пирамиды продавливания во внецентренно нагруженных прямоугольных фундаментах при 0,5 (b — bc) □h0,pl
рmax — максимальное краевое давление на грунт от расчетной нагрузки, приложенной на уровне верхнего обреза фундамента (без учета веса фундамента и грунта на его уступах);
при расчете внецентренно нагруженного фундамента в плоскости эксцентриситета
при расчете в перпендикулярной плоскости, а также для центрально-нагруженного фундамента
Средний периметр пирамиды продавливания um в формуле (1) заменяется средним размером проверяемой грани bm и вычисляется по формулам:
при b — bc □ 2h0,pl (см. черт. 10) bm = bc + h0,pl ; (7)
при b — bc □ (см. черт. 11) bm = 0,5 (b + bc) , (8)
где bc — размер сечения колонны или подколонника, являющийся верхней стороной рассматриваемой грани пирамиды продавливания.
2.10. При действии на фундамент изгибающих моментов в двух направлениях расчет на продавливание выполняется раздельно для каждого направления.
2.11. Рабочую высоту h0,pl центрально-нагруженных, внецентренно нагруженных квадратных и прямоугольных фундаментов можно определить по графику прил. 1, составленному на основании условия 1.
2.12. Рабочую высоту h0,pl внецентренно нагруженных фундаментов можно определить также по формулам:
при 0,5 (b — bc) > h0,pl (см. черт. 10)
(9)
где безразмерная величина r = Rbt / pmax ;
cl = 0,5 (l — lc), cb = 0,5 (b — bc) ;
при 0,5 (b — bc) □ h0,pl (см. черт. 11)
2.13. Высота ступеней назначается в зависимости от полной высоты плитной части фундамента, которую можно получить добавлением толщины защитного слоя к рабочей высоте плитной части фундамента h0,pl и приведением полной высоты h к модульному размеру.
Высоту ступеней рекомендуется назначать в соответствии с табл. 4 (см. п. 4.7).
2.14. Вылеты ступеней фундамента определяются расчетом но продавливание в соответствии с положениями п. 2.9. Вылет нижней ступени c1 (черт. 12) можно определить, предварительно задавшись шириной второй ступени b1 из условия
F □ Rbt h01 bm1 . (11)
Черт. 12. Схема образования пирамиды продавливания в нижней ступени прямоугольных железобетонных фундаментов
Величина силы F и величина среднего размера грани пирамиды продавливания первой ступени bm1 принимаются равными:
F = A01 pmax ; (12)
при b — b1 □ 2h01 bm1 = b1 + h01 ; (13)
при b — b1 □ 2h01 bm1 = 0,5 (b + b1 0 , (14)
где А01 — площадь многоугольника a1b1u1d1e1g1, равная
А01 = 0,5b (l — l1 — 2h01) — 0,25 (b — b1 — 2h01)2 ; (15)
при b — b1 — 2h01 □ 0 последний член формулы (15) не учитывается.
2.15. Вылет нижней ступени с1 можно получить при условии равенства вылетов с1 = с2 (см. черт. 12) по формуле
Вылеты ступеней, при условии их равенства в двух направлениях (например, с1 = с2), рекомендуется определять с помощью прил. 2, где приведены модульные размеры вылетов ступеней с для фундаментов из бетона класса В15 (Rbt = 0,75 МПа и □b2 = 1). При бетоне других марок и других значений □b2 величины максимальных давлений грунта рmax умножаются на отношение □b2 Rbt/0,75, где величина Rbt — в МПа.
2.16. Вылет нижней ступени c1 принимается не более величин, указанных в прил. 3.
2.17. Вылет второй ступени фундамента определяется расчетом на продавливание аналогично вылету нижней ступени (пп. 2.14, 2.15). При этом можно предварительно задаться размерами в плане третьей ступени пересечением линии АВ (см. черт. 12) с линией, ограничивающей высоту второй ступени, по формулам:
l2 = (l — 2c1 — lc)h3 / (h2 + h3) + lc ; (17)
b2 = (b — 2c2 — bc)h3 / (h2 + h3) + bc . (18)
Окончательные размеры ступеней назначают с учетом модульности размеров фундаментов в соответствии с табл. 4 и пп. 4.4, 4.7.
2.18. Для некоторых частных случаев соотношений размеров ступеней проверка несущей способности плитной части производится следующим образом :
а) центрально- и внецентренно нагруженные прямоугольные фундаменты с верхней ступенью, одна из сторон которой l1 □ lc + 2h2, а другая b1 □ bc + 2h2 (черт. 13).
Черт. 13. Схема образования пирамиды продавливания в прямоугольных железобетонных фундаментах с верхней ступенью размерами, при которых одна из сторон ступени l1 □ lc + 2h2, а другая b1 □ bc + 2h2
Расчет на продавливание производится из условия
F □ Rbt (h01 bm1 + h2 bm2) . (19)
Величина F вычисляется по формуле (3), величины bm1 и bm2 принимаются равными:
bm1 = b1 + h01 ; (20)
bm2 = 0,5 (b1 + bc) ; (21)
Aо — площадь многоугольника abcdeg, равна
Ao = 0,5b (l — lc — 2h0,pl) — 0,25 (b — b1 — 2h01)2 , (22)
где h01 — рабочая высота нижней ступени фундамента.
Если 0,5 (b — b1) □ h01, то последний член формулы (22) не учитывается;
б) центрально- и внецентренно нагруженные прямоугольные фундаменты, имеющие в двух направлениях разное число ступеней (черт. 14).
Черт. 14. Схема образования пирамиды продавливания
в прямоугольных железобетонных фундаментах,
имеющих в двух направлениях разное число ступеней
Расчет на продавливание производится из условия
F □ Rbt [(h01 + h2) bm + h3 bc ] . (23)
Величина силы F определяется по формуле (3). Величина среднего размера грани пирамиды продавливания bm принимается равной
bm = bc + h01 + h2 ; (24)
Ao — площадь многоугольника abcdeg, равна
Ao = 0,5b (l — lc — 2h0,pl) — 0,25 [b — bc — 2(h01 + h2)]2 . (25)
Если 0,5 (b — bc) □ h01 + h2, то последний член формулы (25) не учитывается.
Расчет на продавливание по схеме 2
2.19. Расчет на продавливание центрально- и внецентренно нагруженных стаканных фундаментов (низких) квадратных и прямоугольных в плане рот высоте подколонника, удовлетворяющей условию hcf — dp □ 0,5 (lcf — lc) (см. черт. 7), производится на действие только расчетной продольной силы Nc, действующей в уровне торца колонны:
на продавливание фундамента колонной от дна стакана;
на раскапывание фундамента колонной.
2.20. Расчетная продольная сила Nс, действующая в уровне торца колонны, определяется из условия
где □ — коэффициент, учитывающий частичную передачу продольной силы N на плитную часть фундамента через стенки стакана и принимаемый равным
□ = (1 — 0,4Rbt Ac/N), но не менее 0,85, (27)
где Rbt — расчетное сопротивление бетона замоноличивания стакана принимается с учетом коэффициентов условий работы □b2, □b9 по табл. 15 СНиП 2.03.01-84;
Ac = 2(bc + lc) dc- площадь боковой поверхности колонны, заделанной в стакан фундамента.
2.21. Проверка фундамента по прочности на продавливание колонной от дна стакана при действии продольной силы Nc (черт. 15) производится из условия
Nc □ bl Rbt bm (h0,p — dp) / Ao , (28)
где Rbt — принимается по п. 2.8;
Ao — площадь многоугольника abcdeg (см. черт. 15), равная
Ao = 0,5b (l — lp — 2h0,p) — 0,25 (b — bp — 2h0,p)2 ; (29)
bm = bp + ho,p . (30)
В формулах (29) и (30) :
ho,p — рабочая высота пирамиды продавливания от дна стакана до плоскости расположения растянутой арматуры;
bp, lp — размеры по низу меньшей и бульшей сторон стакана (см. черт. 15).
Черт. 15. Схема образования пирамиды продавливания в стаканном фундаменте от действия только продольной силы
2.22. Проверка фундамента по прочности на раскалывание от действия продольной силы Nc (черт. 16) производится из условий:
при bc / lc □ Ab / Al Nc □ (1 + bc / lc) □ □g Al Rbt ; (31)
при bc / lc □ Ab / Al Nc □ (1 + lc / bc) □ □g Ab Rbt ; (32)
где □ — коэффициент трения бетона по бетону, принимаемый равным 0,75;
□g — коэффициент, учитывающий совместную работу фундамента с грунтом и принимаемый равным 1,3; при отсутствии засыпки фундамента грунтом (например, в подвалах) коэффициент принимается равным 1;
Al, Ab — площади вертикальных сечений фундамента в плоскостях, проходящих по осям сечения колонны параллельно соответственно сторонам l и b подошвы фундамента, за вычетом площади стакана фундамента (см. черт. 16).
Черт. 16. Площади вертикальных сечений Аl и Ab при раскалывании стаканного фундамента от действия только продольной силы
В формуле (31) bс/bl должно быть не менее 0,4, а в формуле (32) lc/bc — не более 2,5.
2.23. Из расчетов на продавливание и раскалывание по пп. 2.21 и 2.22 принимается бульшая величина несущей способности фундамента.
В случае неармированного стакана фундамента дополнительно производится расчет на продавливание внецентренно нагруженных стаканных фундаментов квадратных и прямоугольных в плане от верха стакана по схеме 1 (см. черт. 9, 10) из условия (1). При этом величина расчетного сопротивления бетона осевому растяжению принимается с коэффициентом, равным 0,75.
Источник