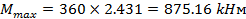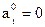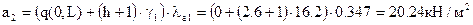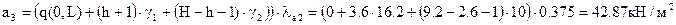- 20.2.2. Расчет тонких (гибких) заанкеренных стенок (ч. 2)
- Б. ТОНКАЯ СТЕНКА С ДВУМЯ АНКЕРАМИ
- Строим силовой многоугольник
- Силовой и веревочный многоугольники. Графическое определение равнодействующей для плоской произвольной системы сил
- Силовой и веревочный многоугольники. Графическое определение равнодействующей для плоской произвольной системы сил
- Построение силового и веревочного многоугольников
20.2.2. Расчет тонких (гибких) заанкеренных стенок (ч. 2)
Б. ТОНКАЯ СТЕНКА С ДВУМЯ АНКЕРАМИ
Двуханкерная неразрезная стенка, рассчитываемая по схеме Блюма–Ломейера, представляет собой статически неопределимую балку. Как и при одноанкерной стенке, расчет ведется графоаналитическим методом упругой линии, предложенным для стенок с двумя анкерами А. Ф. Новиковым.
Пример 20.3. Требуется определить то же, что и в примере 20.2 и для тех же заданных условии, только для стенки с двумя анкерами.
Решение. Графоаналитический расчет тонкой стенки с двумя анкерами (рис. 20.8). На первом этапе расчета (рис. 20.8, а—в), как и ранее, строим эпюры давления грунта на стенку, силовой и веревочный многоугольники. Специфика расчета состоит в отыскании постоянного положения замыкающей веревочного многоугольника, которое удовлетворит принятым опорным условиям, что проверяется последующим построением упругой линии стенки. Последняя, будучи касательной к продольной оси стенки в точке приложения силы E‘p , должна проходить через верхнее и нижнее опорные закрепления А и В.
Направление замыкающей (рис. 20.8, г) находим следующим образом. Продлеваем первый луч веревочного многоугольника до пересечения с горизонтальной линией, проходящей через верхнее крепление (точка А). Полученная ордината представляет собой в масштабе, определяемом соотношением (20.1), консольный изгибающий момент в стенке, который не зависит от работы остальной части балки и поэтому при всех последующих расчетах остается неизменным. Дальнейшее направление ломаной замыкающей задаем двумя прямыми, одна из которых, проходит на участке между опорами A и В, а другая — на участке от опоры В до точки С (точки приложения силы Е‘p ).
При первой попытке положение этих прямых можно принять таким, чтобы ординаты эпюры моментов на опоре В, в пролетной и заглубленной частях были равны между собой ( yB = y1 = у2) . Верхний участок получаем соединением точки В с точкой A.
Далее, принимая полученную эпюру моментов за фиктивную нагрузку, строим упругую ось стенки, отвечающую выбранному положению замыкающей. Для этого вновь строим силовой (рис. 20.8, е) и веревочный (рис. 20.8, д) многоугольники. Веревочный многоугольник и представляет собой искомую упругую ось стенки.
Проведя замыкающую упругой линии через точки А и В, проверяем, является ли она одновременно касательной к веревочному многоугольнику в точке приложения силы E‘p , т.е. соблюдаются ли исходные предпосылки метода Блюма—Ломейера. Указанное условие в данном примере не соблюдено, поэтому вносим поправки в положение замыкающей на рис. 20.8, д. Для этого изменяем ординаты эпюры моментов на опоре В, в пролетной и заглубленной частях стенки.
Необходимую прибавку ординат на уровне нижней опоры ΔMB и на уровне нижнего конца стенки ΔMC (рис. 20.8, д) находим по формулам:


здесь H2 — полюсное расстояние многоугольника фиктивных сил (рис. 20.8, е); h1 и h2 — расстояния соответственно от верхнего и нижнего анкеров до точки С; SB и SC — отклонения последнего луча упругой линии от замыкающей соответственно на уровне опоры В и точки C (в масштабе длин); знак SB и SC принимается отрицательным при отклонениях в сторону засыпки и положительным при противоположном направлении.
Соединяя точки В‘, С‘, А (рис. 20,8, д), получаем новое положение замыкающей А‘ё. Пересечение этой замыкающей с веревочной кривой в точке D определяет точку приложения силы Е‘p .
Критерием правильности поправки, внесенной в положение замыкающей, служит упругая ось (рис. 20.8. к), построенная по суммарной эпюре моментов (рис. 20.8, д).
Полную глубину забивки определяем так же, как и для стенки с одним анкером, по формулам (20.8) и (20.2). Для определения усилий в анкерах ( RA и RB ) новое положение замыкающей А‘ё проводим на веревочном многоугольнике (рис. 20.8, г), для чего вычисляем добавочные ординаты ΔyB и ΔyC на уровне нижнею анкера и точки С по формулам:
Реакции в анкерах отсекаем в многоугольнике сил (рис. 20.8, в) лучами, соответствующими этому положению замыкающей.
Расчетный изгибающий момент определяем по максимальной ординате суммарной эпюры моментов (рис. 20.8, д) по формуле (20.10), а расчетное анкерное усилие по формуле (20.11). В результате расчета получаем следующие величины: t0 = 4 м; Mmax = 103 кН·м; E‘p = 140 кН; RA = 25 кН; RB = 212 кН:

M = 103 · 0,8 = 82,4 кН·м;
Как видно из результатов расчета стенок с одним анкером (рис. 20.6) и с двумя анкерами (рис. 20.8), при прочих равных условиях введение второго анкера значительно уменьшает изгибающий момент в стенке, при этом несколько сокращается глубина забивки стенки.
Сорочан Е.А. Основания, фундаменты и подземные сооружения
Источник
Строим силовой многоугольник
Масштаб силового многоугольника (рис. 2г) выбираем таким образом, чтобы сумма всех активных сил
действующих справа налево графически выразилась отрезком длиной около 10…..15 см. Это соответствует масштабу М1:100. Полюс силового многоугольника О1 размещаем на вертикали, проходящей около середины этого отрезка, а полюсное расстояние η принимаем равным примерно его половине.
полюсное растояние η= 720 кН = 7.2м
Затем на нижней параллельной линии , смещенной на расстояние 20 мм в обратную сторону откладываем в том же масштабе отрезки, соответствующие пассивным силам
Полюсную точку О2 также смещаем на 20 мм вниз от точки О1. Соединив полюсы О1 и О2 лучами с отрезками, выражающими активные и пассивные силы, получим силовой многоугольник (рис. 2 г).
3.12 Строим веревочный многоугольник
Веревочный многоугольник строим параллельным переносом лучей с силового многоугольника на поле горизонтальных линий действия сил Еi . Первый луч из точки О1 проводим до действия силы на расстоянии примерно равным полюсному расстоянию и второй луч из полученной точки пересечения до линии действия силы Е2 и.т.д. (рис.2 д). При этом первый луч (отмеченный значком S ) продлевают до пересечения с горизонтальной линией, проходящей на отметке крепления анкеров к шпунтовой стенке ( в точке А на рис. 2 д).
Замыкающую веревочного многоугольника (штрихпунктирная линия) проводим через точку А таким образом, чтобы максимальная величина изгибающего момента в пролетной части стенки У1.
3.15 Определяем глубину погружения стенки
Точка В пересечения замыкающей с веревочным многоугольником (рис.2 д) определяет необходимую глубину забивки стенки от дна
lo = 9.3м. Полную глубину вибропогружения или забивки шпунта от дна l принимаем равной
Так как шпунтины выпускают длиной кратной 1 м их длины принимаем
3.16 Вычисляем максимальный изгибающий момент
Числовое значение максимального изгибающего момента на один погонный метр шпунтовой стенки определяем по формуле
где η –полюсное расстояние на силовом многоугольнике, выраженное в масштабе сил кН
У1 — расстояние , получаемое на веревочном многоугольнике в линейном масштабе расчетной схемы больверка, м.
3.17 Определяем усилие в анкерной тяге.
Параллельным переносом замыкающей с верёвочного прямоугольника (рис 2д) на силовой (рис 2г) получаем величину усилия в анкерной тяге на один погонный метр набережной Ra, kH/m (отрезок от начала силового многоугольника до точки пересечения его с замыкающей в масштабе сил).
в = 83.68 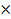
Источник
Силовой и веревочный многоугольники. Графическое определение равнодействующей для плоской произвольной системы сил

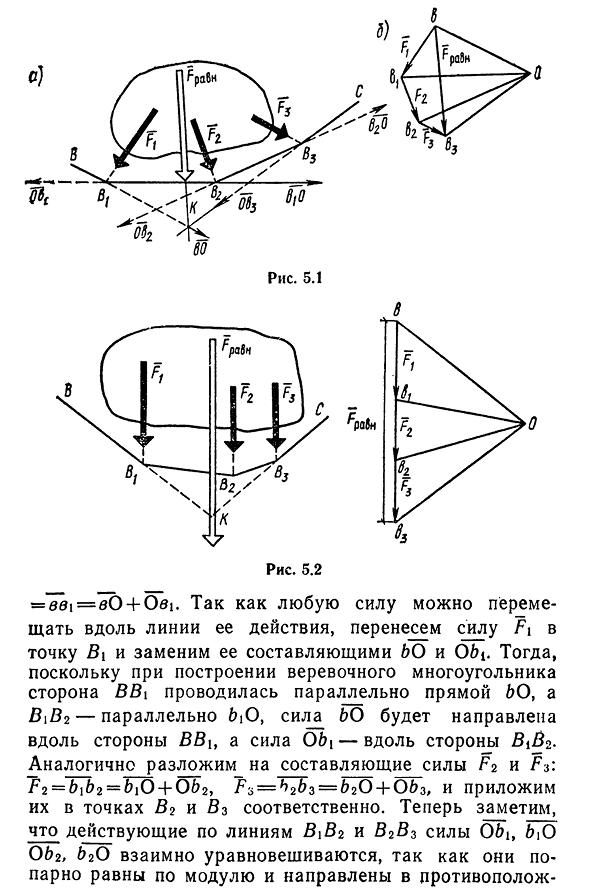

Силовой и веревочный многоугольники. Графическое определение равнодействующей для плоской произвольной системы сил
- Мощность и веревочный многоугольник. Одна из проблем со статистикой, как описано в§1.1, состоит в том, чтобы найти любую систему, полученную в результате силы. Эту проблему можно решить, применяя эти силы непрерывно (см.§1.5). Однако этот способ громоздок и неудобен, особенно при применении большого
количества сил. Рассмотрим более удобный и простой способ нахождения системы произвольных плоских сил (включая систему параллельных сил). Пусть на свободные твердые тела действует плоская система произвольных сил
Давайте теперь выясним положение Людмила Фирмаль
линии действия равнодействующей системы сил. Выталкивает любую точку O, которая не существует на стороне многоугольника или ее продолжение в плоскость многоугольника и соединяет ее со всеми вершинами многоугольника. Затем возьмем любую точку(рис. 5.1, а) провести через нее линию, параллельную линии S, и перейти к точке пересечения с линией действия силы Fi в точке B. Затем
провести линию, параллельную линии, от точки Bi до пересечения с линией действия силы F2 в точке B2, и так далее. Построенная таким образом полилиния BB^b2b3c называется канатным полигоном, и ее название происходит от того, что гибкие нити фиксируются в точках B и C, а нити B2 и B3 фиксируются в точках B и C. Теперь мы докажем, что результирующая линия действия FpaBH фактически проходит
- через точку / S_iz силового многоугольника(рис. 5.1, б) найти, что Fi= 48и = — eei=eb+Oei. Так как любую силу можно перемещать вдоль линии ее действия, то передадим силу Fi в точку Bi, и попробуем заменить составляющие Fi и Obi тогда, так как при построении каната из полигона сторона B I перешла к линии Bo, Bic2-параллельная био сила направляется вдоль стороны Bi и O bi, BI2. Аналогично разложим компоненты силы F2 и F3: F2=bib2=biO+Ob2, F3=h2b3—b2O+Ob3 и приложим их соответственно в 2 и 3 точках.
Теперь сила, действующая на линии b iB2 и B 2b3obi, b, 0Ob2, B 2 o, заключается в том, что модуль равен, и поскольку он направлен в противоположном направлении, он уравновешен друг с другом.- 4-480 Обратная сторона. Поэтому с помощью этих полномочий можно меняться.■ В результате этой системе сил соответствуют две силы
B и obz, направленные вдоль крайних сторон BBI и B3C, а именно канатный многоугольник. <. 0-3>. (5.1) Таким образом, через эту Людмила Фирмаль
точку их результат, или то же самое, проходит через результирующий Фпабх системы этой силы. Поскольку полученные правила графического определения являются общими, то применима и система параллельных сил, направленных как на одну, так и на разные стороны. Эти три параллельные силы показаны на рисунке. 5.2
Источник
Построение силового и веревочного многоугольников
Сложив эпюры активного и пассивного давления грунта, определяем окончательный вид эпюры давления (рисунок 3).
Производится расчет сил схемы нагрузок. Для этого эпюра нагрузок разбивается на полосы 0,5¸1,0 м, которые заменяются силами Ei, приложенными в центрах тяжести этих полос.
Величины сил Ei численно равны площади соответствующих полос. Площади полос определенные в ACAD сведены в таблицу 2.
На основании этих данных строится силовой многоугольник: масштаб 1 мм – 2,5 кН, полюсное расстояние η = 200 кН = 80 мм, полюс О размещается на вертикали около середины значения активных сил (рисунок 3).
| №№ | Ei, кН | №№ | Ei, кН | №№ | Ei, кН |
| 16,69 | 44,87 | 48,95 | |||
| 22,31 | 48,50 | 93,44 | |||
| 28,64 | 52,25 | 137,91 | |||
| 19,46 | 56,00 | 182,38 | |||
| 22,80 | 13,25 | 226,84 | |||
| 41,12 | 5,14 | 130,10 |
Строится веревочный многоугольник: прямая, параллельная нулевому лучу силового многоугольника, пересекает линию действия первой силы, из этой точки проводится луч первой силы, из точки пересечения проводится луч второй силы и так далее.
Строится замыкающая прямая АВ. Точка А распложена на пересечении нулевого луча силового многоугольника и линии влияния анкерной реакции. Точка В на веревочном многоугольнике строится таким образом, чтобы максимальная величина ординаты изгибающего момента в нижней части эпюры была на 10% меньше максимальной величины ординаты изгибающего момента в пролетной части стенки (z1=1,1·z2)
Точка B на веревочном многоугольнике определяет необходимую глубину забивки шпунтовых свай to = 4,9 м (рис. 3)
3.3 Определение величины анкерной реакции и максимального изгибающего момента в стенке при проектной нагрузке q (0,L) = 40 кН/м 2
Пересечение замыкающей с эпюрой моментов определяет положение силы 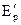
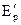
Величина 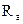
Ra q = 212,2 кН– величина усилия в анкерной тяге на один погонный метр набережной.
Определяем значение максимального изгибающего момента в стенке:
M q = η·z1 = 200·1,38 = 276 кНм.
Рисунок 3
3.4 Построение эпюр активного и пассивного давления грунта
при отсутствии нагрузки, q (0,L) = 0 кН/м 2
Графоаналитический расчет одноанкерного больверка при отсутствии нагрузки на кордоне приведен на рисунке 4
Активное давление:
на поверхности грунта засыпки:
на уровне воды акватории выше поверхности воды:
на уровне воды акватории ниже поверхности воды:
на уровне проектного дна:
ниже уровня проектного дна:
на отметке низа шпунта:

Источник