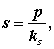Основные положения проектирования гибких фундаментов



До сих пор, при расчете гибких фундаментов совместно с грунтовым основанием применяются эти две теории, которые в соответствии с классификацией Н.А.Цытовича /4/ называются:
теория местных упругих деформаций, основанная на гипотезе Винклера-Циммермана;
теория общих упругих деформаций, основанная на гипотезе упругого полупространства.
Теория местных упругих деформаций основана на гипотезе прямой пропорциональности между давлением и местной осадкой:

Из приведенного выражения следует, что осадка поверхности основания возникает только в месте приложения давления p и поэтому модель грунта можно представить в виде совокупности отдельно стоящих пружин (рис.1,а).
В действительности на реальном грунтовом основании понижение поверхности наблюдается и за пределами нагруженного участка (рис.1,б), образуя упругую лунку. Кроме того, коэффициент постели не учитывает размеров подошвы фундамента и не является постоянной величиной для данного грунта. Как показали исследования, данная гипотеза дает достаточно достоверные результаты для слабых грунтовых оснований.
Несмотря на отмеченные недостатки метод местных упругих деформаций, на котором базируются расчеты балок и плит на упругом (Винклеровском) основании, позволяя более экономично проектировать гибкие фундаменты с учетом податливости грунтового основания, до сих пор находит довольно широкое применение при расчете ленточных и плитных фундаментов и дает достаточно достоверные результаты, если при выборе величины коэффициенты постели учитывается площадь передачи нагрузки и величина среднего давления га грунт по подошве.
Следует отметить, что широко применяемая на практике программа «Лира/Scad» /5/ для расчета строительных конструкций включает модуль позволяющий рассчитывать гибкие фундаменты, базирующийся в свою очередь на методе местных упругих деформаций.
Теория общих упругих деформаций основана на гипотезе упругого полупространства, согласно которой основание работает как сплошная однородная упругая среда, ограниченная сверху плоскостью и, бесконечно простирающаяся вниз и в стороны. Деформационные свойства упругой среды характеризуются величиной модуля деформации, который не зависит от величины нагрузки под подошвой фундамента, в отличие от коэффициента постели. При нагружении такого упругого основания деформации имеют место не только в месте приложения нагрузки, но и за ее пределами (рис.1,б), что и наблюдается под реальными фундаментами.
Деформация упругого основания по теории общих упругих деформаций определяется с использованием решений теории упругости.
Исходными уравнениями деформаций основания в теории общих упругих деформаций являются:
— для случая плоской деформации – решение Фламана


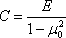
Опыт применения данного метода, накопленный при поектировании большого количества ответственных сооружений, показал, что упругое полупространство во многих случаях хорошо моделирует грунтовое основание.
Однако и этот метод имеет определенные недостатки. Основной его характеристикой является модуль деформации. Существующие лабораторные методы не позволяют определять его с достаточной точностью. Испытания грунта в компрессионных приборах дают заниженные значения модуля деформации. Оказалось, кроме того, что модуль деформации имеет различные значения для условий плоской и пространственной деформации.
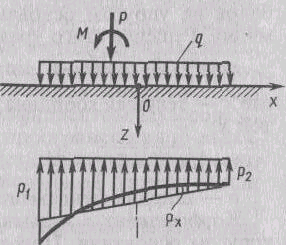
Кроме того распределение реактивных давлений по теории упругости обладает существенным недостатком: под краями фундамента они становятся бесконечно большими (рис. 2), чего в опытах не наблюдается, поэтому во многих случаях эта модель основания приводит к завышенным внутренним усилиям (моменты и поперечные силы) в конструкции фундаментов.
Источник
Ф.12.6. Какие теории применяются при расчете гибких фундаментов?



При расчете гибких фундаментов совместно с грунтовым основанием применяются две теории:
— теория местных упругих деформаций, основанная на гипотезе Винклера-Циммермана;
— теория общих упругих деформаций, основанная на гипотезе упругого полупространства.
Теория местных упругих деформаций основана на гипотезе прямой пропорциональности между давлением и местной осадкой:
где s — упругая осадка грунта в месте приложения давления интенсивностью p в рассматриваемой точке; ks — коэффициент упругости основания, именуемый «коэффициентом постели».
Из приведенного выражения следует, что осадка поверхности основания возникает только в месте приложения давления p и поэтому модель грунта можно представить в виде совокупности отдельно стоящих пружин (рис.Ф.12.6,а).
В действительности на реальном грунтовом основании понижение поверхности наблюдается и за пределами нагруженного участка (рис.Ф.12.6,б), образуя упругую лунку. Кроме того, коэффициент постели не учитывает размеров подошвы фундамента и не является постоянной величиной для данного грунта. Как показали исследования, данная гипотеза дает достаточно достоверные результаты для слабых грунтовых оснований.
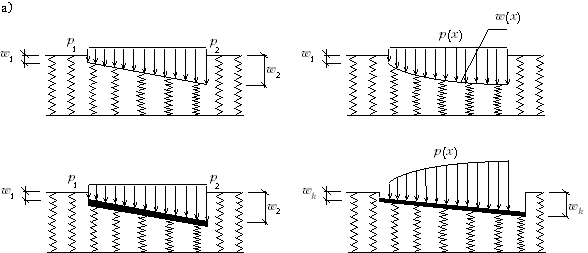  |
| Рис.Ф.12.6. Деформация поверхности грунта основания: а — по теории местных упругих деформаций; б — по теории общих упругих деформаций |
Теория общих упругих деформаций основана на гипотезе упругого полупространства, согласно которой основание работает как сплошная однородная упругая среда, ограниченная сверху плоскостью и бесконечно простирающаяся вниз и в стороны. Деформационные свойства упругой среды характеризуются величиной модуля деформации, который не зависит от величины нагрузки под подошвой фундамента, в отличие от коэффициента постели. При нагружении такого упругого основания деформации имеют место не только в месте приложения нагрузки, но и за ее пределами (рис.Ф.12.6,б), что и наблюдается под реальными фундаментами.
Деформация упругого основания по теории общих упругих деформаций определяется с использованием решений теории упругости.
Источник
Ф.12.6. Какие теории применяются при расчете гибких фундаментов?
При расчете гибких фундаментов совместно с грунтовым основанием применяются две теории:
— теория местных упругих деформаций, основанная на гипотезе Винклера-Циммермана;
— теория общих упругих деформаций, основанная на гипотезе упругого полупространства.
Теория местных упругих деформаций основана на гипотезе прямой пропорциональности между давлением и местной осадкой:
где s — упругая осадка грунта в месте приложения давления интенсивностью p в рассматриваемой точке; ks — коэффициент упругости основания, именуемый «коэффициентом постели».
Из приведенного выражения следует, что осадка поверхности основания возникает только в месте приложения давления p и поэтому модель грунта можно представить в виде совокупности отдельно стоящих пружин (рис.Ф.12.6,а).
В действительности на реальном грунтовом основании понижение поверхности наблюдается и за пределами нагруженного участка (рис.Ф.12.6,б), образуя упругую лунку. Кроме того, коэффициент постели не учитывает размеров подошвы фундамента и не является постоянной величиной для данного грунта. Как показали исследования, данная гипотеза дает достаточно достоверные результаты для слабых грунтовых оснований.
  |
| Рис.Ф.12.6. Деформация поверхности грунта основания: а — по теории местных упругих деформаций; б — по теории общих упругих деформаций |
Теория общих упругих деформаций основана на гипотезе упругого полупространства, согласно которой основание работает как сплошная однородная упругая среда, ограниченная сверху плоскостью и бесконечно простирающаяся вниз и в стороны. Деформационные свойства упругой среды характеризуются величиной модуля деформации, который не зависит от величины нагрузки под подошвой фундамента, в отличие от коэффициента постели. При нагружении такого упругого основания деформации имеют место не только в месте приложения нагрузки, но и за ее пределами (рис.Ф.12.6,б), что и наблюдается под реальными фундаментами.
Деформация упругого основания по теории общих упругих деформаций определяется с использованием решений теории упругости.
Ф.12.7. Влияет ли конструкция фундамента на использование имеющихся решений теории упругости для определения деформации поверхности основания?
Все конструкции фундаментов условно можно разделить на три группы по характеру напряженно-деформированного состояния грунта в их основании:
1. Фундаментные балки, имеющие достаточно большую длину и нагрузку, которая не изменяется от сечения к сечению. Основание под такими фундаментами находиться в условиях плоской деформации, так как если вырезать полосу шириной b (рис.Ф.12.7,а) в поперечном направлении, то грунт основания будет находится в аналогичных условиях с любой соседней подобной полосой. Все деформации грунта основания возникают только в плоскости приведенной схемы.
2. Фундаменты дымовых труб, газгольдеров, градирен, имеющие круглое очертание в плане, передают на основание нагрузки, которые вызывают осесимметричное напряженно-деформированное состояние в грунте основания (рис.Ф.12.7,б).
 |
| Рис.Ф.12.7. Условия работы грунта основания: а — плоская деформация; б — осесимметричная деформация; в,г — пространственная деформация |
3. Конструкции фундаментов, в основании которых грунт находится в условиях пространственного напряженно-деформированного состояния. Такие фундаменты применяются в большинстве случаев в конструкциях элеваторов, атомных и тепловых электростанций и представляют собой прямоугольные или квадратные плиты. Деформации грунта основания различны по всем трем направлениям (рис.Ф.12.7,в,г).
Исходными уравнениями деформаций основания в теории общих упругих деформаций являются:
для случая плоской деформации — решение Фламана
для случая пространственной и осесимметричной деформации — решение Буссинеска
где s — осадка упругой полуплоскости или упругого полупространства; P — сосредоточенная сила для случая пространственной деформации и p — погонная полосовая нагрузка для условий плоской деформации: 
Источник
10.4. Основные положения проектирования гибких фундаментов
Ленточные фундаменты большой длины, загруженные колоннами, расположенными на значительных расстояниях, балки на грунте, а также большинство плитных фундаментов относятся к гибким фундаментам.
В отличие от жестких фундаментов, собственные деформации которых ничтожно малы по сравнению с деформациями грунта, деформации гибких фундаментов соизмеримы с деформациями основания, в результате этого гибкий фундамент и его основание работают под нагрузкой совместно, образуя единую систему, а реактивное давление грунта изменяется по сложному закону, существенно отличающемуся от линейного. Определение этого давления из расчета совместного деформирования фундамента с основанием является основной задачей при проектировании гибких фундаментов. Задача довольно сложная, поскольку в общем случае реактивное давление на фундамент зависит от жесткости фундамента, его размеров и формы, характеристик деформируемое™ основания, величины, характера и расположения нагрузки. Сюда следует добавить и жесткость надземной части сооружения.
Подробно методы расчеты балок и плит на упругом основании изложены в курсах «Строительная механика» и «Железобетонные конструкции». Ниже будут рассмотрены основные положения этих расчетов, а также их особенности, связанные со спецификой работы грунтов как линейно деформируемых тел.
Расчет ленточных фундаментов. В задачу расчета гибкого ленточного фундамента входят определение реактивного давления грунта по подошве фундамента, вычисление внутренних усилий, действующих в фундаменте, установление размеров поперечного сечения фундамента и его необходимого армирования.
При расчете реактивного давления грунта гибкий ленточный
фундамент рассматривается как балка на упругом основании, изгибающаяся под действием приложенных к ней внешних нагрузок. Если пренебречь трением между подошвой фундаментной балки и грунтом основания, что идет в запас прочности, дифференциальное уравнение ее изгиба можно представить в виде
где EL— жесткость балки; z — прогиб балки в точке с координатой х; рх — реактивное давление в той же точке.
В дифференциальном уравнении (10.18) имеются две неизвестные функции: одна — уравнение изогнутой оси балки z=f(х), вторая — закон распределения реактивных давлений грунта рх=f(х), поэтому решение может быть получено лишь при условии составления второго уравнения, в котором будут связаны между собой осадки различных точек балки и реактивное давление грунта.
В зависимости от гипотезы, принятой для установления второго уравнения, различают два основных метода расчета балки, лежащей на упругом основании: метод местных упругих деформаций и метод упругого полупространства. Оба метода базируются на одноименных моделях грунтового основания, рассмотренных в § 5.2, там же определена и область их применения для практических инженерных расчетов.
Уравнение (10.18) содержит жесткость фундамента Е1, что требует предварительного назначения размеров его сечения. Это делают исходя из схемы линейного распределения реактивных усилий, принимая равномерное или трапециевидное распределение давления по подошве. Поясним сказанное на примере.
Рис. 10.21. Предварительный подбор сечения фундаментной балки
На рис. 10.21 показана фундаментная балка, загруженная системой сил, в результате чего по ее подошве действует реактивное давление грунта рх, изменяющееся по какому-то сложному закону. Заменяя криволинейную эпюру распределения реактивных давлений рх линейной трапециевидной, определяем краевые значения давления р1и р2 по формуле внецентренного сжатия (5.7), которая для рассматриваемого случая будет иметь вид
А — площадь подошвы фундаментной балки; МO — момент всех сил относительно центра тяжести подошвы фундаментной балки г
Определив краевые значения прямолинейной эпюры давлений P1 и Р2 загружаем ею рассматриваемую фундаментную балку, как внешней нагрузкой, и по правилам строительной механики строим эпюру изгибающих моментов Мх. Определив максимальное значение Мх, находим необходимый по условию прочности момент сопротивления балки WX, а уже по нему подбираем предварительное сечение фундаментной балки и устанавливаем ее жесткость Еl.
Расчет по методу местных упругих деформаций. Как указывалось в § 5.2, предпосылкой расчета гибких фундаментных балок по этому методу является гипотеза о том, что осадка в данной точке основания не зависит от осадки других точек и прямо пропорциональна давлению в этой точке (гипотеза Фусса — Винклера), что выражается зависимостью (5.3)
где СZ— коэффициент пропорциональности, называемый коэффициентом постели, ориентировочно равный: (0,3. 1). 10 4 кН/м3 при очень слабых грунтах, (1. 3).10 4 кН/м3 при слабых грунтах, (3. 8) • 10 кН/м при грунтах средней плотности; Z — осадка в точке определения реакции рх.
Подставляя эту зависимость в дифференциальное уравнение (10.18), получим
Eld 4 z/dx 4 = -СZZ,. (10.19)
Уравнение (10.19) известно как дифференциальное уравнение изгиба балок на упругом основании по методу местных упругих деформаций. Решение этого уравнения имеет вид

где х — текущая координата; z — прогиб балки в точке с координатой х;
=
Ь — ширина фундаментной балки.
Коэффициент а называют линейной характеристикой балки на упругом основании. При l 3 — как длинные гибкие. Естественно, что указанные границы условны поэтому в практических расчетах допустимы небольшие отклонения.
Постоянные интегрирования С1, С2. Сз и С4 определяются изначальных условий деформирования, которые зависят от категории гибкости балки. Так, одним из начальных условий деформирования для короткой жесткой балки, загруженной в центре сосредоточенной силой, будет постоянство деформации грунта вдоль всей ее длины (z=const), а в случае длинной гибкой балки при таком же загружении начальным условием деформирования будет отсутствие прогиба на ее концах (Z-1/2=Z+1/2=0).
Беря последовательно производные от выражения (10.20), определяют необходимые для конструирования фундаментной балки значения изгибающих моментов Мx и поперечных сил QX в различных ее сечениях. Если уточненные по известным значениям Мx и QX размеры сечения балки значительно меняют ее жесткость, то расчет повторяется.
Модель местных упругих деформаций рекомендуется применять для расчета гибких фундаментных балок, работающих в условиях плоской задачи на сильно сжимаемых грунтах (Е 2 ) — коэффициент жесткости основания, кПа; R — расстояние от точки приложения силы Р до точки, в которой определена осадка ZX , м.
При определении осадок поверхности основания от действия равномерно распределенных нагрузок уравнения (10.21) и (10.22) интегрируются по площади загружения.
Решая дифференциальное уравнение изогнутой оси балки (10.18) совместно с одним из уравнений (10.21) или (10.22), находят реактивный отпор грунта по подошве гибкого фундамента, изгибающие моменты и поперечные силы, действующие в его сечениях.
Практические расчеты ведутся чаще всего с использованием готовых таблиц, которые составлены для фундаментных балок различной относительной гибкости, при различном характере и размещении нагрузок.
Относительная гибкость фундаментной балки, работающей в условиях плоской задачи, характеризуется показателем гибкости t, определяемым по формуле (5.1):

Если фундаментная балка работает в условиях пространственной задачи, показатель гибкости определяется по формуле
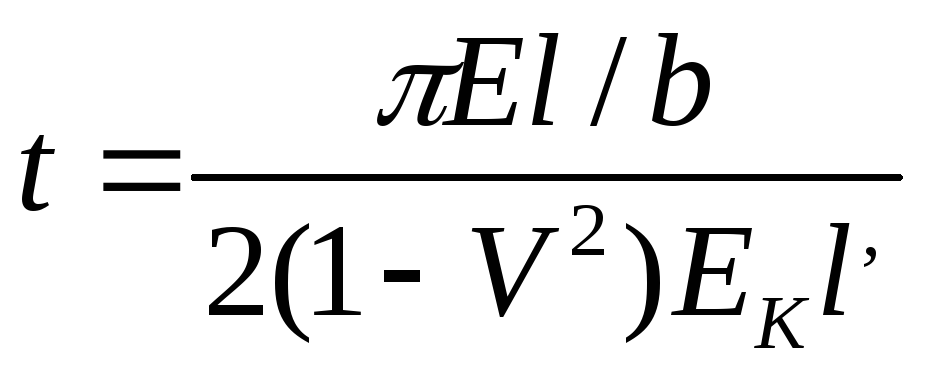
где Е — модуль деформации грунта, кПа; v — коэффициент Пуассона грунта; Еk— модуль упругости материала балки, кПа; l, b — полудлина и полуширина фундаментной балки, м; h — высота балки, м.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник