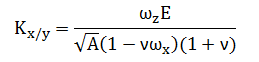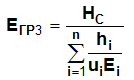Коэффициент постели для плитного фундамента

6.5. РАСЧЕТ ПЛИТНЫХ И ЛЕНТОЧНЫХ ФУНДАМЕНТОВ ПОД КОЛОННЫ

6.5.1. Общие положения

Расчет ленточных и плитных фундаментов, работающих на изгиб, проводится с учетом совместной работы конструкции и грунтового основания согласно теории конструкций на упругом основании. В этом случае предположение о линейном распределении реактивных давлений уже не может рассматриваться как достаточно точное, так как изгиб конструкции изменяет распределение этих давлений и, следовательно, отражается и на усилиях в балках и плитах. Линейное распределение давлений используется лишь для предварительного определения сечений конструкций.

6.5.2. Предварительное назначение размеров сечений

Предварительное назначение размеров сечений рассмотрим на примере ленточного фундамента под колонны, исходя из схемы линейного распределения реактивных давлений. Изгибающие моменты в каждом сечении ленты определяются по формуле

где M_l — момент в данном сечении от площади эпюры реактивных давлений, расположенной левее данного сечения; ΣP_il_i — сумма моментов для данного сечения от нагрузок, передаваемых колоннами, расположенными левее сечения (здесь Р_i — нагрузка от колонны i ; l_i —расстояние от колонны до сечения); ΣМ_i — сумма внешних моментов, передаваемых колоннами, расположенными левее данного сечения.

За положительное направление моментов принимается направление по часовой стрелке.

Таким образом, изгибающие моменты определяются простейшим способом по схеме статически определяемой балки. Не рекомендуется пользоваться расчетом статически неопределимой неразрезной балки, нагруженной трапецеидальной эпюрой давлений, при котором опорные реакции оказываются отличными от расчетных нагрузок, передаваемых на балку колоннами; кроме того, такой расчет сложнее. Использование схемы неразрезной балки оправдано лишь в случае, если жесткость верхнего строения очень велика и не позволяет смещаться опорным точкам колонн нелинейно относительно друг друга. В этом случае учитывается перераспределение внешней нагрузки по колоннам исходя из учета жесткости верхнего строения.

6.5.3. Расчет фундаментных балок и плит как конструкций на упругом основании

Для учета влияния изгиба на распределение реактивных давлений используется одно из двух предположений.

1. Основание работает согласно гипотезе коэффициента постели (Винклера). Эта гипотеза предполагает, что осадка какой-либо точки (элемента) поверхности основания s пропорциональна давлению р , приложенному в той же точке, т.е. что p = k_ss . Коэффициент k_s , Па/м, называется коэффициентом постели. Осадка данной точки (элемента) зависит только от давления, приложенного в этой точке, и не зависит от давлений, действующих по соседству (рис. 6.32, а).

2. Основание работает как среда, к которой применимы формулы теории упругости, связывающие напряжения и осадки. Грунт принимается за однородное упругое тело, бесконечно простирающееся вниз и в стороны и ограниченное сверху плоскостью (упругое полупространство), а соответствующее предположение называется гипотезой упругого полупространства. Поверхность упругого полупространства деформируется не только непосредственно под нагрузкой, но и по соседству с ней (рис. 6.32, б). Деформационные свойства грунта характеризуются в основном модулем деформации Е₀ , МПа.

Согласно гипотезе коэффициента постели, грунт лишен распределительной способности, т.е. деформации соседних с нагрузкой элементов поверхности грунта отсутствуют. Коэффициент постели для данного типа основания предполагается величиной, не зависящей от площади фундамента (в действительности — зависит).

В гипотезе упругого полупространства распределительная способность преувеличена. Модуль деформации является характеристикой, представляющей одновременно как упругие, так и остаточные деформации. При многократном приложении нагрузки остаточные деформации исчезают, модуль общей деформации Е₀ переходит в модуль упругости Е , значительно больший, чем Е₀ , При ширине фундамента примерно от 70 см до 7 м значение модуля деформации меняется незначительно. При превышении ширины 7 м модуль деформации заметно возрастает.

6.5.4. Связь между расчетными значениями модуля деформации и коэффициента постели

Между расчетными значениями модуля деформации Е₀ и коэффициентом постели, исходя из приравнивания осадок, вычисленных по той и другой гипотезе, устанавливается связь

Значение k₀ определяется по рис. 6.33 в зависимости от отношения сторон прямоугольного фундамента α, его опорной площади А и коэффициента Пуассона грунта ν₀ , принимаемого для песков ν₀ = 0,3, для суглинков и супесей ν₀ = 0,35, для глин ν₀ = 0,4.

Осадки жесткого прямоугольного фундамента на однородном основании определяются по формуле

где Р — суммарная центрированная нагрузка на фундамент.

Осадки жесткой плиты лишь немного меньше (на 7 %) средних осадок гибкой плиты при равномерной нагрузке.

Расчеты по обеим гипотезам, даже при использовании формулы (6.126), дают, как правило, различные результаты в отношении изгибающих моментов в конструкции и ее изгиба. Только для узких балок при α ≥ 10 можно подобрать отличное от определяемого формулой (6.127) значение коэффициента постели, при котором результаты расчета будут близки. Однако при равномерной нагрузке или при нагрузке, приближающейся к ней, получить близкие результаты расчета при любом соотношении между E₀ и k невозможно. Формула соотношения между Е₀ и k , для узких балок шириной В имеет вид:

Гибкие фундаменты в настоящее время рассчитываются преимущественно по гипотезе упругого полупространства. Этот расчет при фундаментах большой опорной площади, в десятки или сотни квадратных метров, дает, однако, преувеличенное значение осадки, изгиба и изгибающих моментов, так как гипотеза игнорирует уплотнение грунта с глубиной, вызванное действием его собственного веса. Кроме того, при больших опорных площадях грунт под фундаментом сжимается в основном без возможности бокового расширения, что не учитывается при опытном определении модуля деформации штампом.

Чтобы приблизить расчетные условия к действительным, при больших опорных площадях используют схему, согласно которой основание представляет собой сжимаемый слой, подстилаемый несжимаемым основанием. Удобно также использовать схему однородного полупространства с повышенным модулем деформации так, чтобы расчет по этой схеме давал значение, равное ожидаемой осадке.

Сорочан Е.А. Основания, фундаменты и подземные сооружения

Источник

По какому методу рассчитывать фундаментную плиту и коэффициенты постели?

Страница 1 из 3

1

2

3

>

Здравствуйте, уважаемые формучане!

Хотелось бы в который раз поднять тему о расчете фундаментных плит и коэффициентах постели. «В который раз», потому что данная тема поднималась на форуме не единожды, причем на данной ветке можно встретить сообщения 8-10 летней давности. По этой причине хотелось бы внести ясность в некоторые вопросы, руководствуясь современным опытом проектирования специалистов, а их на форуме не мало.

Начну с того, что передо мной встала задача – запроектировать плитный фундамент под жилой 3-х этажный дом. Из программ более-менее владею Лирой, поэтому считать решил в ней.

Итак.фундамент представляет собой плиту, толщиной 250мм, с несущими стенами техподполья (толщина стен также 250мм).
Собрал нагрузки на верх стен по СП, выполнил в Лире расчетную схему пластинами, приложил нагрузки (схема приведена во вложении).

Затем было необходимо смоделировать основание плиты.
В Лире основание моделируется при помощи коэффициентов постели. Каким образом правильно задать эти коэффициенты, какой из 3-х предложенных методов подсчета К.П. наиболее корректен? – с этими вопросами я и зашел на двг-форум… (на свою голову)))

Итак, я перешерстел все темы о коэффициентах постели двг-форума, просмотрел пособия по расчетам, статьи и т.п.

Самыми полезнымина данный момент мне показались следующие данные:
1)А.Г.Шашкин, К.Г.Шашкин:
Статьи http://www.georec.narod.ru/mag/T2/1.htm , http://www.georec.spb.ru/journals/03/20/20.htm
Пособие «Взаимодействие здания и основания: методика расчета и практическое применение при проектировании».
2) Созанович М.Е.:
«О некоторых аспектах расчетов фундаментов» (есть в даунлоаде — http://dwg.ru/dnl/3540 )
3) Многочисленные комментарии специалистов по данной теме (в случае чего, могу и их привести)

Исходя из вышеизложенного материала, я сделал следующий вывод: для того чтобы считать основания зданий и сооружений получать корректные результаты, на данный момент наиболее логично использовать следующие модели расчета:

1. Двухконстантная модель Пастернака (с двумя коэффициентами постели)
2. Моделирование объемными конечными элементами (ОКЭ)

Прошу спецов подтвердить, правильный ли я сделал вывод??

Теперь вопросы по моделям:
1) Модель Пастернака:
— считаю коэф-ты постели вручную по формулам из пособия Созановича(либо по Шашкину) и вбиваю их по всей площади плиты в Лире, верно так делать?
— нужны ли законтуренные элементы и каков их смысл? (судя по Созановичу не нужны, Шашкин пишет что их неучет –это ошибка в расчете)
— как определить грубину сжимаемой толщи? По СП 50-101-2004, пункт 5.5.41,по схеме линейно-деформируемого полупространвства?

2) Объемные конечные элементы (ОКЭ)
— какие задавать боковые границы и нижнюю границу? Методом подбора, до тех точек, в которых напряжения «до» и «после» загружения плитой не изменятся?
— моделировать нужно в 2 стадии? Сначала грунт загрузить собственным весом, а потом добавить плиту?
— нужно ли каким-то образом моделировать контакт «основание-плита» ?

Буду очень признателен за ответы, хотя бы на какие-то вопросы! Заранее Спасибо!

Источник

Задание граничных условий (связей) для фундаментных плит в горизонтальной плоскости

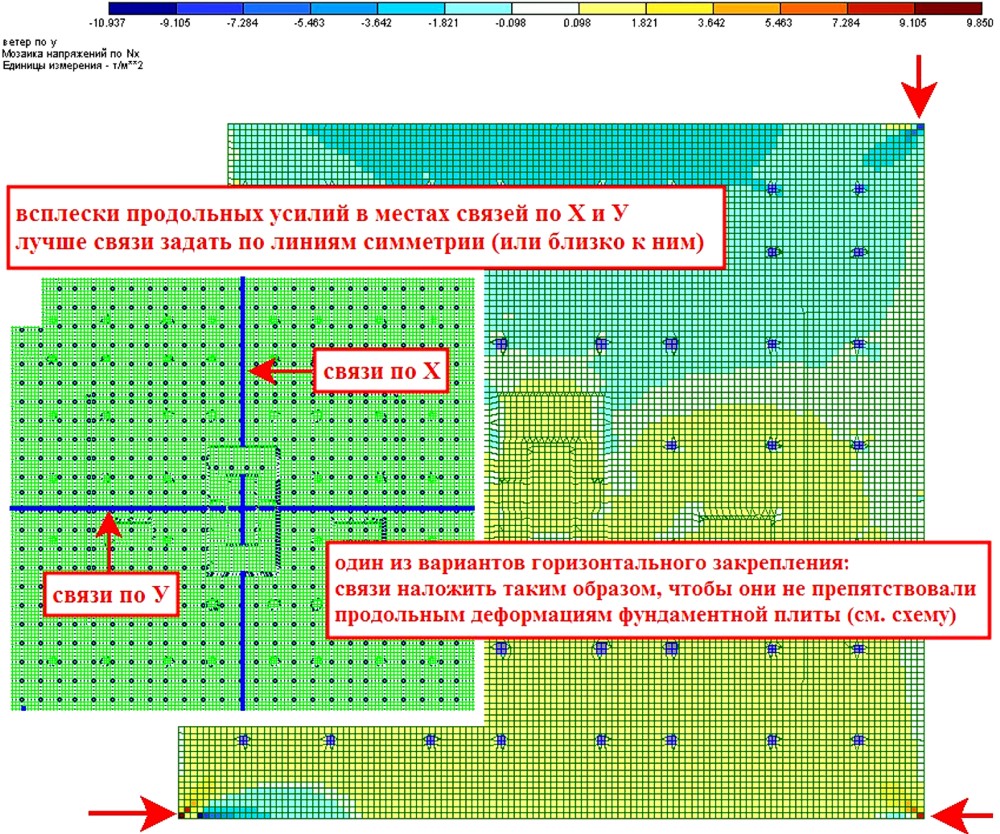
Фундаментные плиты зданий, как правило, моделируются в виде пластинчатых элементов на упругом основании. Роль вертикальной связи выполняют граничные условия виде коэффициентов постели. Для обеспечения геометрической неизменяемости здания в горизонтальных направлениях (вдоль осей X и Y) следует наложить граничные условия в плоскости фундаментной плиты. Как известно, для обеспечения геометрической неизменяемости тела на плоскости достаточно наложить 3 связи, не пересекающиеся в одной точке. Бывает, что на практике расчетчики закрепляют фундаментную плиту в только трех узлах. Подобное закрепление может привести к резким всплескам усилий в местах наложения связей, а соответственно и армирования:

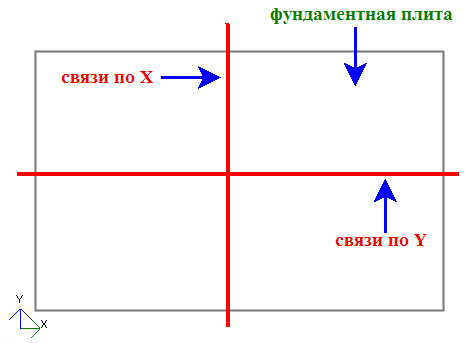
Если фундаментная плита имеет оси симметрии, то связи лучше задавать по линиям симметрии. Для линии параллельной оси X следует запретить перемещение по направлению оси Y и наоборот. Т.е. по следующей схеме:

Наложенные таким образом связи не будут приводить к всплескам усилий в конечных элементах фундаментной плиты, а плита при этом остается неподвижной в горизонтальной плоскости. При этом при подборе армирования также будет учтена мембранная группа усилий.

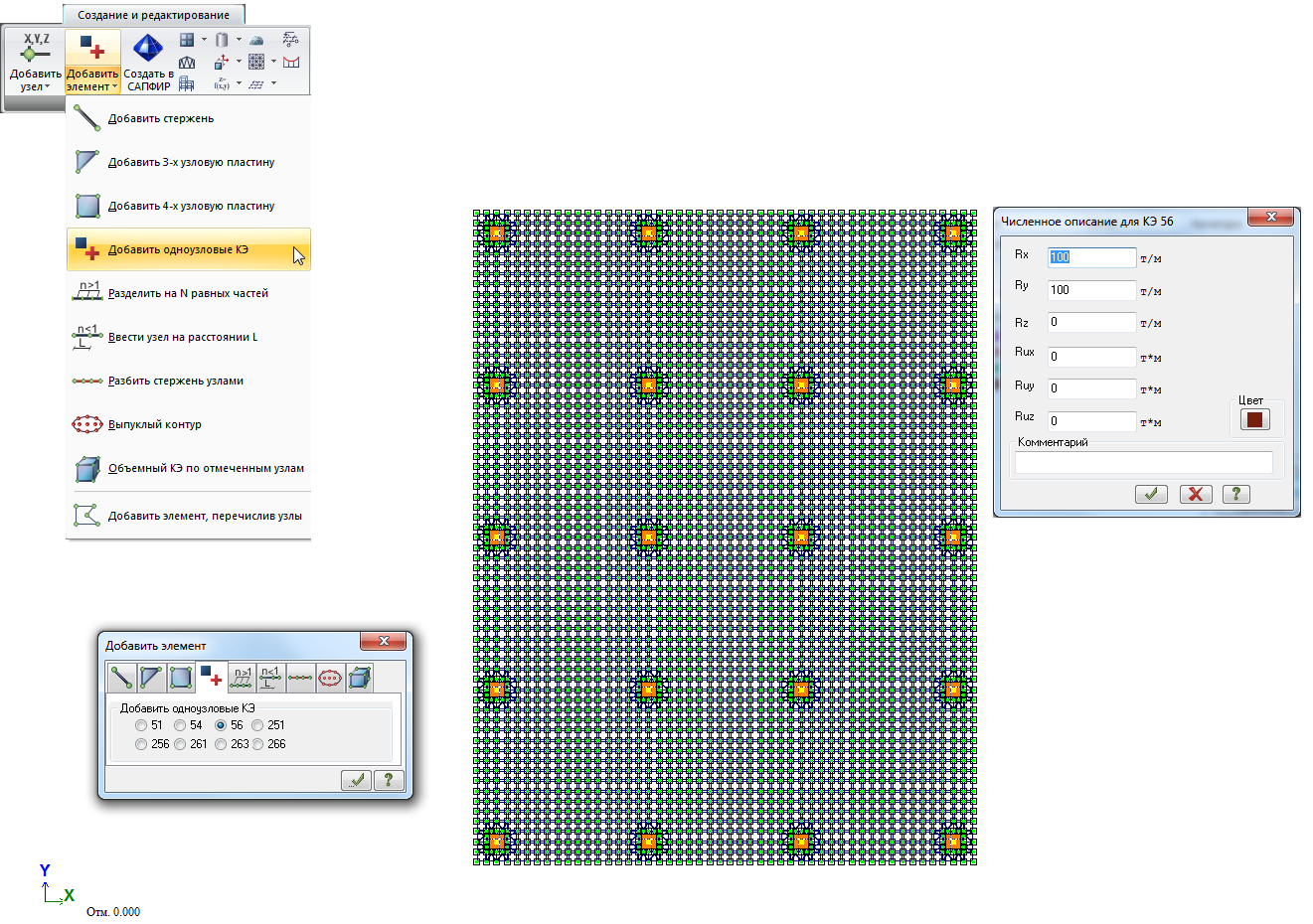
Другой вариант задания граничных условий — применения связей конечной жесткости КЭ 56. При использовании данного варианта во все узлы фундаментной плиты вводятся одноузловые конечные элементы 56 типа. В описании типа жесткости данного конечного элемента следует задать жесткостные характеристики в горизонтальном направлении — Rx и Ry:

Значения Rx и Ry можно определить, зная количество n элементов 56 типа (равно количеству узлов фундаментной плиты, в которые вводятся эти элементы) и величину сдвиговой жесткости основания K_x/y:

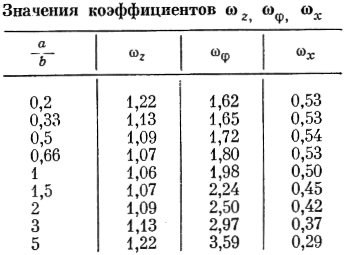
Жесткость основания в горизонтальной плоскости Kx/y может быть определена из решения статической задачи о штампе на упругом основании [1] стр. 25:

где А — площадь фундамента; Е — модуль деформаций грунта основания; ν — коэффициент Пуассона грунта основания, ωz и ωx — коэффициенты, зависящие от соотношения сторон фундамента a и b.

Другой подход к определению K_x/y базируется на решении задачи о колебаниях штампа на упругом основании [2] стр. 97:

где А — площадь фундамента, Cz — коэффициент упругого равномерного сжатия.

Этот подход включен в нормы на проектирования [3].

Источник

Коэффициент постели для плитного фундамента

Рис.3. Задание нагрузок на основание

Система выполняет следующие операции:

— определение полей осадок грунтового и свайного оснований для существующих и проектируемых зданий в соответствии с заданными нагрузками и инженерно-геологическими условиями грунтов;
— определение границы сжимаемой толщи в соответствии с условиями различных нормативов;
— вычисление коэффициентов постели упругого (грунтового) основания С1 и С2 в соответствии с моделями грунта Винклера и Пастернака;
— вычисление разностей осадок, а также перекосов фундаментов существующих зданий с учетом влияния проектируемых сооружений.

Для выполнения вычислений производится триангуляция областей, ограниченных заданными контурами. В узлах триангуляции, шагом которой можно управлять, вычисляются все необходимые параметры.

В соответствии с приложенными нагрузками определяются осадки грунта под проектируемыми фундаментами и свайными ростверками. При этом учитываются положения действующих в Украине и России норм по проектированию оснований зданий и сооружений и свайных фундаментов – ДБН В.2.1-10:2009, СНиП 2.02.01-83, СП 50-101-2004, СП 22.13330.2011 и СП 24.13330.2011.

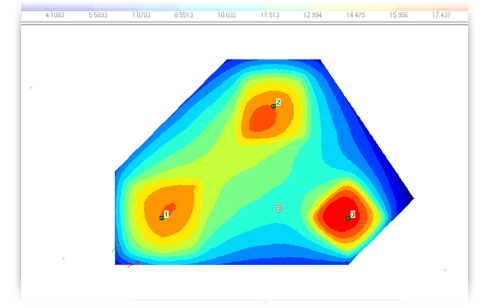
Вычисление осадок S производится методом послойного суммирования с использованием схемы линейно-деформируемого полупространства (задача Буссинеска) (Рис.4).

Рис.4. Изополя осадок и эпюра вертикального напряжения

Достижение границы сжимаемой толщи H_С регулируется выполнением условия σ_zp = k*σ_zg с помощью задаваемого коэффициента глубины сжимаемой толщи k.

Вычисляются следующие слагаемые:

Если собственный вес грунта на уровне подошвы больше среднего давления под подошвой, то осадка S = 0.8*W3, иначе осадка S = 0.8*(W1 + W2).

Вычисление коэффициентов постели

Для вычисления коэффициентов постели используются усредненные (в пределах зафиксированной глубины сжимаемой толщи H_С) значения модуля деформации E_ГР и коэффициента бокового расширения m_ГР. Эти значения вычисляются по формулам.

Коэффициент постели С1 вычисляется тремя методами.

Метод 1. Коэффициент постели С1 вычисляется на основании усредненных значений E_ГР и m_ГР по формуле:

Метод 2. Коэффициент постели С1 вычисляется по формуле Винклера:

Метод 3. Для определения коэффициента постели С1 используется формула метода 1. Отличие состоит в том, что для определения усредненного модуля деформации Е_ГР3 вводится поправочный коэффициент u к величине модуля деформации i–того подслоя. Этот коэффициент изменяется от u1=1 на уровне подошвы фундамента до u_n=12 на уровне уже вычисленной границы сжимаемой толщи. Принято, что коэффициент u изменяется по закону квадратной параболы:

Кроме того, принимается, что дополнительное вертикальное напряжение по глубине распределено равномерно. Тогда

Суть метода 3 изложена в работах и состоит в том, что в действительности модуль деформации грунта по глубине нарастает. Не учет этого факта приводит к неоправданно завышенным значениям осадок, а, следовательно, и к заниженным значениям коэффициента постели С1.

Для методов 1 и 3 коэффициент постели С2 вычисляется по формуле:

Для метода 2 коэффициент постели С2 не вычисляется.

По результатам работы программы выполняется построение полей осадок, границ сжимаемой толщи, коэффициентов постели Пастернака и Винклера. Выполняется построение эпюр вертикальных напряжений в любой точке приложенной нагрузки (Рис. 4, 5).

Рис.5. Эпюра вертикального напряжения при различном распределении нагрузки вдоль свай

Расчет осадки свайного фундамента, как условного, строго в соответствии с нормами выполняется при K1, K2 = 0 и K3 = 1.

Если внешняя нагрузка на свайный фундамент задана на несколько уровней, то эпюра напряжений от нее будет иметь ступенчатый вид, отражающий уровни приложения соответствующих долей нагрузки. Так на Рис. 5-а показана эпюра вертикального напряжения при К1 = 0, К2 = 0, К3 = 1. На Рис. 5-б показана эпюра вертикального напряжения при К1 = 0.05, К2 = 0.9, К3 = 0.05. Причем, К2 разбит еще на 10 подуровней (количество подуровней может изменяться по желанию пользователя). На Рис. 5-в показана эпюра вертикального напряжения при К1 = 0.1, К2 = 0.6, К3 = 0.3.

По результатам вычисления осадок предоставляется возможность вычисления их разностей между существующими и проектируемыми фундаментами. Определяются также перекосы фундаментов существующих зданий, возникающие от проектируемых сооружений (Рис. 6). Перекосы вычисляются между парами точек, заданных пользователем.

Рис.6. Таблицы осадок и перекосов

Система ГРУНТ входит в состав таких программных комплексов как ЭСПРИ 2013, ЛИРА-САПР и МОНОМАХ-САПР.

ВЫВОДЫ. Система ГРУНТ позволяет производить экспертную оценку осадок, кренов и перекосов сооружений, как на естественном, так и на свайном основании и оценивать влияние проектируемых новых зданий на существующую окружающую застройку.

Авторы: Д.А. Городецкий, В.П. Максименко, Д.В. Медведенко, Е.Б. Стрелец-Стрелецкий
ООО ЛИРА САПР, Киев.

Источник