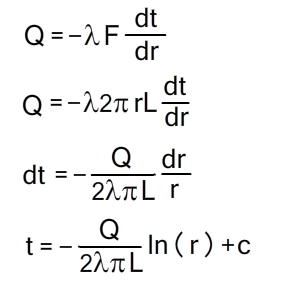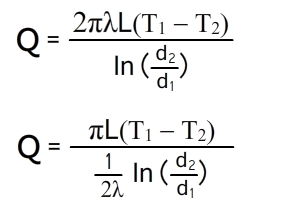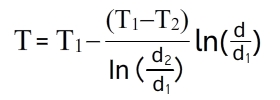Количество тепла проходящего через стену

Теплопроводность через стенку

Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.

Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача — величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической — по логарифмическому закону, т.е.

Q = const и T = f(x) — линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).

Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.

Теплопередача через непроницаемую стенку включает в себя следующие процессы:

1. теплоотдачу от горячей среды к стенке;
2. теплопроводность внутри стенки;
3. теплоотдачу от стенки к холодной среде.

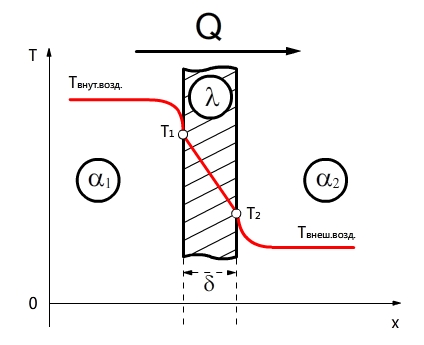
Теплопередача через плоскую стенку (граничные условия первого рода)

Теплопроводность — первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.

Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.

Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.

Тепловой поток Q [Вт] — это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).

Поверхностная плотность теплового потока рассчитывается по формуле:

где Q — тепловой поток [Вт]; F — площадь стенки [м 2 ].

На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:

где δ = dx — толщина стенки, λ

λ/δ; [Вт/м 2 *К] — коэфициент тепловой проводности стенки.

а обратная величина —

R = δ/λ; [м 2. К/Вт] — термическое сопротивление стенки.

Для теплового потока формулу так же можно представить в виде:

Общее количество теплоты проходящее через площадь стены S за время t можно представить как:

Распределение температуры в плоской стенке

Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C₁; T=C₁х+С₂ (1). Определим С₁ и С₂ через граничные условия.

При х=0 T=T₁, подставим в уравнение (1) и получим T₁=С₂.
При х=δ T=T₂, подставим в уравнение (1) и получим T₂=С₁*δ+С₂, T₂=С₁*δ+T₁, получим: С₁=(Т₂-T₁)/δ. Теперь подставим в уравнение (1) найденные С₁ и С₂, получим следующее распределение температуры в нашей стене:

Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:

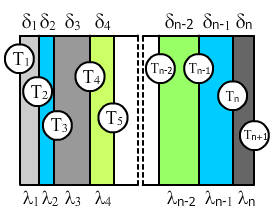
Теплопроводность через многослойную стенку

Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λ_i и разной толщиной δ_i.

Термическое сопротивление стенки считается так:

Для теплового потока формула будет иметь вид:

Температура на границе слоя вычисляется по следующей формуле:

Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:

Эквивалентная теплопроводность многослойной стенки:

Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)

Теплопередача — это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.

Коэффициент теплоотдачи α, Вт/(м 2 ·К) — это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.

Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:

q = k * (T_{возд.внутри} — T_{возд.снаружи}); Вт/м 2

Коэффициент теплопередачи для n слойной стенки:

Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:

Тогда общее термическое сопротивление теплопередаче будет равно:

Температуры на поверхности стенки можно определить по формулам:

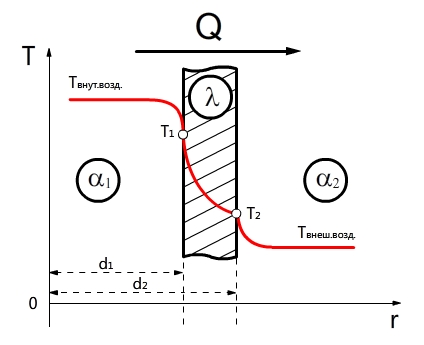
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)

Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа «труба в трубе», кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.

Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:

Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:

Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:

Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F₁ или внешней F₂ поверхности трубы. При этом расчетные формулы принимают следующий вид:

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Источник

Количество тепла проходящего через стену

Чтобы понять, как считать теплопроводность — необходимо представить материал в виде вымышленной стены. На практике такие стены будут реальными. Данная статья поможет нам рассчитать теплопотери стены. Сложив все теплопотери стен — получим теплопотери всего дома. Но это только один фактор из трех составляющих теплопотерь дома. Не забывайте про вентиляцию и излучение тепла. О них поговорим в других статьях.

t₁, t₂ — точки температур. L — толщина стены. S — площадь стены.

Теплопроводность представляет собой количество теплоты, которое проходит в единицу времени через единицу толщины слоя материала.

Если быть точнее! То это отношение поверхностной плотности теплового потока к температурному градиенту.

Температурный градиент — это произведение толщины стенки материала на разность температур между противоположными плоскостями одной стенки.

Температурный градиент = L х ( t₁ — t₂ ).

Плотность теплового потока — это количество теплоты в единицу времени. Количество теплоты измеряется в Калориях. О калориях поговорим ниже.

Сначала я Вам покажу формулу нахождения теплопроводности и связи между ними.

λ — Коэффициент теплопроводности.

t₁,t₂ — температуры стенки по разные стороны. Измеряется либо в Цельсиях [°C] либо в Кельвинах [K].

[ Вт / (м•°С) ] либо [ Вт / (м•K) ]

В редких случаях за место (Вт) может использоваться (Калория).

L — Толщина стенки, измеряется в метрах(м).

Q — Количество теплоты, измеряется в калориях(K) или в ваттах(Вт).

Эталоном значения одной калории является: Количество теплоты необходимое для того, чтобы нагреть один грамм воды на 1 градус Цельсия или Кельвина, при атмосферном давлении (101325 Па).

1 Дж = 0,2388 калорий 1000 Калорий = 1 кКалория = 1,163 Ватт • час 1 Калория = 4,1868 Дж

Для глубокого понимания коэффициента теплопроводности, нужно понимать, как находят количество теплоты. То есть нам нужно найти количество теплоты, которое расходуется между наружными плоскостями одной стены. Мы фактически находим потерянное тепло через стену.

Данная формула помогает нам найти проходящее количество теплоты в сквозь стену.

Также еще выражаются в такой форме:

R — Температурное сопротивление, измеряется: (м 2 • °С) / Вт, или: (м 2 • K) / Вт

Q — Количество теплоты. Измеряется в Ваттах (Вт) или Калориях (К)

t₁,t₂ — температура стенки по разные стороны. Измеряется либо в Цельсиях [°C] либо в Кельвинах [K].

S — площадь стенки, измеряется в квадратных метрах (м 2 ). Площадь находится умножением высоты на длину стенки. S = a • b.

Чем больше значение λ, тем большей теплопроводностью обладает вещество. В общем случае теплопроводность для данного вещества не является величиной постоянной: для твердых тел λ зависит от температуры, а для жидких и газообразных — еще и от давления.

Для металлов (кроме алюминия) теплопроводность с увеличением температуры несколько убывает, что означает, что холодный металл проводит теплоту лучше, чем нагретый. Теплопроводность металлов λ составляет 2,3-420 Вт/(м•К).

Для изоляционных и огнеупорных материалов λ при повышении температуры возрастает. Последнее объясняется тем, что большинство изоляционных материалов не представляют монолитной массы, а являются пористыми телами — конгломератом отдельных частиц с воздушными прослойками между ними. Эти воздушные прослойки уменьшают теплопроводность, но лучистый теплообмен, происходящий в этих прослойках, в итоге увеличивает суммарный теплоперенос при повышении температуры пористого тела. Для таких материалов λ зависит не только от свойств собственно материала, но и от степени его уплотнения, т.е. от плотности. Кроме того, на теплопроводность указанных материалов большое влияние оказывает влажность. С увеличением влажности теплопроводность возрастает. Для влажного материала λ выше, чем для сухого материала и воды, взятых в отдельности. Так, например, для сухого кирпича λ = 0,35 Вт/(м•К), для воды λ = 0,58 Вт/(м•К), а для влажного кирпича λ = 1,05 Вт/(м•К). Это объясняется тем, что адсорбированная в капиллярно-пористых телах вода отличается по физическим свойствам от свободной воды. Поэтому по отношению к такого рода веществам правильнее говорить о так называемой видимой теплопроводности. Теплопроводность теплоизоляционных материалов составляет 0,02—3,0 Вт/(м•К).

Для газов с увеличением температуры теплопроводность также возрастает, но от давления λ практически не зависит, кроме очень низких (менее 2,5 кПа) и очень высоких (более 200 МПа) давлений. Теплопроводность газов колеблется от 0,006 до 0,6 Вт/(м•К).

Для большинства капельных жидкостей теплопроводность находится в пределах 0,09—0,7 Вт/(м•К) и с повышением температуры уменьшается. Вода является исключением: с ростом температуры от 0 до 150 °С теплопроводность возрастает, а при дальнейшем увеличении температуры уменьшается.

У меня дома в квартире, в комнате имеется наружная не утепленная стена площадью ( 2,5 х 5метров ), зимой очень холодно. Температура стены 20 °C. Стена без окна. Определить сколько уходит тепла через стену на улицу зимой, когда на улице температура -30 градусов. Стена кирпичная. Толщина 80 см.

S=2,5 х 5 = 12,5 м 2

t1 = 20 °C, K1 = t1 + 273,15 = 293,15

t2 = -30 °C, K2 = t1 + 273,15 = 243,15

L = 80см = 0,8 метров.

Для кирпича из других источников:

λ = 0,44 Вт/(м•К) в переводе на Цельсия: = 0,44 Вт/(м•°С)

Решение простое: Просто вставляем в формулу имеющиеся значения и занимаемся арифметикой.

Q = 0,44 х (20-(-30))/0,8 х 12,5 = 0,44 х 50/0,8 х 12,5 = 343,75 Вт

Ответ: Теряется тепло стены на 344 Вт.

Если посчитать за месяц, то это будет: 344 Вт х 24 часа х 30 дней = 247,7 кВт•ч.

И это одна только стена столько потребляет! А сколько таких стен может быть?

Конечно, точность расчетов зависит от значения коэффициента теплопроводности для материала, из которого сделана стена. Влажность, тоже имеет значение. Так что этих коэффициентов в инете полным-полно, можете подобрать из различных таблиц.

В целом такой расчет очень даже полезный и почти совпадает с реальными цифрами.

Таблицы я позже приготовлю! В других статьях будут. А так продолжение следует.

Источник

Поверхность стены, термического сопротивления и температуры поверхности контакта кирпича и теплоизоляционного материала

Цель работы: научиться определять количества тепла, проходимое через поверхность стены, термическое сопротивление и температуры поверхности контакта кирпича и теплоизоляционного материала

Теплопроводность в значительной мере зависит от величины пористости, размера и характера пор. У пористых материалов тепловой поток проходит через твердый «каркас» материала и воздушной ячейки. Теплопроводность воздуха очень низкая ─ 0,023 ВТ/(м• о С), а вещества, из которых построен твердый каркас материала, имеют значительно большую теплопроводность. Мелкопористые материалы и материалы с замкнутыми порами обладают меньшей теплопроводностью, чем крупнопористые материалы и материалы с сообщающимися порами. Это связано с тем, что в крупных и сообщающихся порах усиливаются перенос теплоты конвекцией, что и повышает суммарную теплопроводность.

Теплопроводность материалов учитывается при теплотехнических расчетах толщины стен и перекрытий отапливаемых зданий, а также при определении требуемой толщины тепловой изоляции горячих поверхностей и холодильников. Она связана с термическим сопротивлением слоя материала R (м 2 •С/Вт), которое определяется по формуле:

R=h/λ, (1)

где h ─ толщина слоя, см, м; λ ─ теплопроводность слоя материала, Вт/ м 2 •С.

В таблице 1 приведены значения теплопроводности некоторых строительных материалов в воздушно-сухом состоянии.

Таблица 1 – Теплопродность некоторых строительных материалов

Наименование материала	Теплопровод-ность слоя материала, Вт/ м 2 •С	Наименование материала	Теплопроводность слоя материала, Вт/ м 2 •С
Керамический кирпич с технологическими пустотами	0,8	Бетон тяжелый	3,0
Бетон легкий	0,58	Древесноволокнистые плиты	0,08
Пенобетон	0,15	Фибролит	0,14

В таблице 2 для представлены необходимые данные для расчетов различных вариантов.

Таблица 2 – Варианты для расчета количества тепла, температуры поверхности контакта кирпича и теплоизоляционного материал и термического сопротивления

Вари-ант	Материал	d кирпича, см	t1, о С	t2, о С	λ1, Вт/(м• о С)	d1, см
Керамический кирпич с технологическими пустотами	-28	0,7	2,6
Бетон легкий	-27	0,71	2,4
Пенобетон	-26	0,72	2,3
Бетон тяжелый	-25	0,73	2,7
Древесноволокнистые плиты	-24	0,74	2,8
Фибролит	-23	0,75	2,9
Бетон легкий	-27	0,71	2,34
Керамический кирпич с технологическими пустотами	-27	0,65	2,63
Пенобетон	-25	0,71	2,3
Бетон тяжелый	-25	0,72	2,7
Древесноволокнистые плиты	-23	0,73	2,8
Фибролит	-23	0,74	2,88
Керамический кирпич с технологическими пустотами	-27	0,75	2,34
Бетон легкий	-27	0,71	2,64
Пенобетон	-25	0,65	2,22
Бетон тяжелый	-24	0,73	2,3
Древесноволокнистые плиты	-25	0,72	2,7
Фибролит	-23	0,73	2,8
Бетон легкий	-23	0,74	2,88
Пенобетон	-27	0,75	2,34
Бетон тяжелый	-27	0,71	2,64
Древесноволокнистые плиты	-25	0,65	2,22
Фибролит	-27	0,75	2,34
Бетон легкий	-27	0,71	2,64
Пенобетон	-25	0,65	2,22

В качестве примера сделаем расчет для нулевого варианта.

На первом этапе расчетов для определения количества тепла через кирпичную стену воспользуемся формулой:

Условия задачи для нулевого варианта (таблица 2):

Наружная сторона кирпичной стены толщиной d=64см имеет температуруt₁ = -28 о С, внутренняя t₂─ +22 о С (таблица 2). Какое количество тепла проходит через 1 м 2 поверхности стены за 1 час, если теплопроводность кирпича λ=0,8 Вт/(м• о С) (таблица 1). Внимание, при расчетах сокращения не допускаются.

1. Q=225 кДж

На втором этапе расчетов необходимо определить температуру поверхности контакта кирпича и теплоизоляционного материала, если известно, что теплопроводность теплоизоляционного материала λ₁=0,7 Вт/(м• о С), а толщина d₁=2,6определяется по формуле:

Так как Q=Q₁, то225=2520[(22-х)/2,6]или585=2520(22-х).

0,232=22-х; отсюда х=22-0,232=21,68.

2. t_х (температура поверхности контакта кирпича и теплоизоляционного материала)= 21,68 о С.

На третьем этапе расчетов сначала рассчитываем R=h/λдля кирпича,

R_кирп.=64/0,8=80 (м 2 • о С/Вт)

3. R_кирп.=80 (м 2 • о С/Вт),

а затем для теплоизоляционного материала

R_{теплоиз.}=2,6/0,7=3,714 (м 2 • о С/Вт)

4. R_{теплоиз.}= 3,714 (м 2 • о С/Вт)

На четвертом этапе все полученные расчетные данные (подчеркнутые) согласно своего варианта вносим в таблицу 3.

Таблица 3 – Расчетные данные нулевого варианта

1. Q, кДж	2. tх (температура поверхности контакта кирпича и теплоизоляционного материала), о С	3. Rкирп., (м 2 • о С/Вт),	Rтеплоиз. (м 2 • о С/Вт)
21,68	3,714

Вопросы для защиты практического занятия №4

1. От чего в значительной мере зависит теплопроводность?

2. Как проходит тепловой поток?

3. У кого очень низкая теплопроводность?

4. Какие материалы обладают меньшей теплопроводностью и с чем это связано?

5. Что такое термическое сопротивление?

6. Что определяется на первом этапе расчетов, написать формулу?

7. Что определяется на втором этапе расчетов, написать формулу?

8. Что определяется на третьем этапе расчетов, написать формулу?

9. Что определяется на четвертом этапе расчетов, написать формулу?

10. Что определяется на пятом этапе расчетов

Источник