Метод местных упругих деформаций применяемый при расчете гибких фундаментов учитывает

Строй-справка.ру

Отопление, водоснабжение, канализация

Для получения полного решения уравнения (7.6) необходимо к общему решению (7.7) добавить частное решение z, зависящее от нагрузки q0. При условии, если q0 может быть представлена алгебраическим полиномом степени не выше третьей от х, то частное решение может быть найдено с помощью полинома соответствующей степени с помощью метода неопределенных коэффициентов.

Постоянные интегрирования выражения (7.7) определяют из граничных условий.

В общем случае действия на балку различных нагрузок, разбивая балку на определенное количество участков, приходится для каждого из них находить свои значения произвольных постоянных. Это приводит к необходимости для различных, встречающихся на практике, нагрузок составлять и решать большое количество уравнений со многими неизвестными, что существенно усложняет расчет. Однако дальнейшие исследования показали, что в большинстве случаев любую систему нагрузок, приложенных к балке конечной длины, удается заменить системой балок бесконечной длины, прикладывая в их сечениях фиктивные силы и моменты, обеспечивая при этом выполнение граничных условий и заменяя на основании принципа независимости действия сил решение сложной задачи системой простых схем, расчетные усилия для которых известны.

Учет сдвигающих напряжений, вовлекающих в работу ненагруженные зоны грунта рядом с нагруженными, с помощью второго коэффициента постели позволил значительно усовершенствовать метод местных упругих деформаций.

Главное отличие данной модели заключается в том, что основание с двумя коэффициентами постели имеет осадки и за пределами лежащей на нем балки.

Расчет плит с помощью метода местных деформаций значительно сложнее расчета балок.

В настоящее время разработано достаточно большое количество методов расчета, позволяющих получать решение уравнения (7.13) с помощью использования алгебраических полиномов, компенсирующих нагрузок, вариационных методов, конечных элементов и конечных разностей. Разработан целый комплекс программ, дающих возможность проводить расчет плитных фундаментов на ЭВМ с дополнительным учетом касательных напряжений по подошве фундамента, а также жесткости надфундаментных конструкций.

Согласно теории местных упругих деформаций при равномерной нагрузке на балку реакция основания будет одинаковой по всей площади контакта с грунтом, что не подтверждается экспериментальными данными. Аналогичный результат будет получен и при расчете по данному методу жестких фундаментных конструкций.

Еще раз заметим, что метод местных упругих деформаций допускается применять при проектировании гибких фундаментов при наличии в основании слабых грунтов или слоя сжимаемого грунта небольшой мощности.

Рис. 7.2. Схема длинной балки, затру- подстилаемого плотным несжиженнои посередвдеойСосредото,енной маемым.

Источник

Расчет гибких ф. с помощью метода местных деформаций

Теории расчета балок и плит на упругом основании и условия их применимости к расчету гибких фундаментов

Для гибких ф., которые в основном воспринимают изгибающие моменты, образующиеся в результате совместной работы с основанием, предположение о линейном распределении реактивных давлений оказывается неприемлемым, потому что оно зависит от жесткости ф. и податливости грунтового основания.

Замена реальной эпюры контактных давлений линейно распределенной приводит к существенным погрешностям при определении изгибающих моментов и перечных сил.

К гибким ф. можно отнести ленточные и отдельные ж. б. ф., а также сплошные ж. б. плиты и некоторые типы коробчатых ф.

В настоящее время большое распространение при проектировании гибких ф. получили теории расчета балок и плит на упругом основании, которые справедливы для линейно деформируемых оснований, причем наибольшее применение получили следующие методы:

— местных деформаций с постоянным и переменными коэффициентами постели;

— упругого слоя ограниченной толщины на несжимаемом основании;

— упругого слоя с переменным модулем деформации основания по глубине.

Эти теории исходят из предположения о совместности деформации, ф. и грунта, т.е. считается, что перемещение ф. в данной точке контакта равно осадке поверхности грунта.

В основу расчета гибких ф. по этому методу положена гипотеза о том, что осадка в данной точке основания не зависит от осадки других точек и прямо пропорциональна реактивному давлению в этой точке, что выражается зависимостью

где z – осадка основания в точке действия реактивного давления p(x); k_S – коэфф. пропорциональности («коэфф. постели»), Па/м, зависящий от физических свойств грунтов.

Подставляя эту зависимость в дифференциальное уравнение изгиба балки, получим дифференциальное уравнение изгиба балки на упругом основании по методу местных упругих деформаций

EJz IV +bk_Sz=q(x),

где q(x) – внешняя нагрузка на ф.;

EJ – изгибная жесткость ф.;

b – ширина ф.

Для получения полного решения данного дифф. уравнения необходимо к общему решению (при q(x)=0) добавить частное решение, зависящее от q(x).

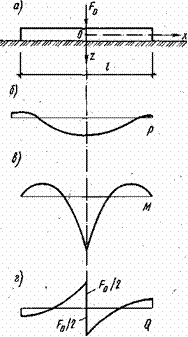
В частности, рассматривая случай загружения бесконечно длинного гибкого ф. сосредоточенной силой, приложенной в середине, получим следующие выражения

z(x)=P/(8EJa 3 )e — a x (cosax+sinax);

M(x)=P/(4a)e — a x (cosax-sinax);

Q(x)=-P/2e — a x cosax,

где a=(k_Sb/(4EJ)) 1/4 – упругая характеристика ф.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Лекции по Основаниям и фундаментам. DOC / Проектирование гибких фун-ов

Проектирование гибких фундаментов

При расчете жестких фундаментов была принята линейная зависимость распределений напряжений под подошвой фундамента. При расчете фундаментов конечной жесткости (гибких фундаментов- балок и плит) условная линейная эпюра распределения напряжений под подошвой гибкого фундамента не приемлема.

В этом случае необходимо учитывать M и Q, возникающие в самой конструкции фундамента, вследствие действия неравномерных контактных реактивных напряжений по подошве фундамента. Не учет возникающих усилий может привести к неправильному выбору сечения фундамента или % его армирования.

Поэтому необходимо решать задачу совместной работы фундаментной конструкции и сжимаемого основания.

Какие же фундаменты считать гибкими?

Гибкие фундаменты — это те, деформации изгиба которых того же порядка, что и осадки этого же фундамента

∆ S(см) ≈ f(см); ∆ S – осадка фундамента (деформация основания)

f – деформация изгиба фундамента

Таким образом, при расчете гибких фундаментов необходимо одновременно учитывать и деформации фундамента и его осадки.

конструкция грунт

При расчете ленточных фундаментов, загруженных неравномерно сосредоточенными силами — необходимо учитывать изгиб в продольном направлении.

Вследствие изгиба фундамента конечной жесткости давление на грунт увеличивается в местах передачи фундаменту сосредоточенных сил и уменьшается в промежутках между этими силами.

Единого метода расчета гибких фундаментов нет, а существует несколько способов.

h

Критерий, определяющий состояние фундамента

> — абсолютно жесткие фундаменты

(Рассматриваются при опирании конструкции стены. Расчитываются гибкие конструкции типа рандбалок, ж/б поясов).

Бесконечно простирающаяся полоса и нагрузка приложена вдоль всей полосы.

Для расчета необходимо рассматривать единичный элемент.

Рассчитываются гибкие ленточные конструкции — фундамент под стены.

(ж/б фундамент под колонну)

Расчет балок по методу

местных упругих деформаций ( гипотеза Винклера).

; где

P_x – интенсивность давления, передающегося на основание (реактивный отпор грунта в т. Х)

Z_x – величина перемещения в т. Х (зависит от жесткости балок, характера распределения нагрузки, размеров балки и деформируемости основания

Впервые этот метод был применён при расчете шпал под ж/дор., тогда считали, что С_z = f (грунта), но потом выяснилось, что С_z = f (грунта и ширины подошвы фундамента)

P_x =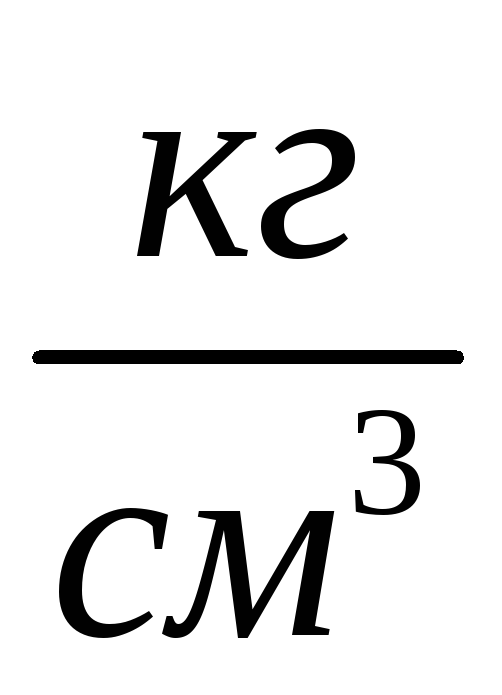; С_z =; Z_x = см

Из сопромата известно уравнение, описывающее изгиб балки:

; ;

Значение Р_х заменяем исходной формулой:

Решая это уравнение мы найдем Z_x :

; А_1, А_2, А_3, А₄ — произвольные постоянные, определяемые из

В конечном итоге находим С_z и Р_х , а следовательно М_х и Q_x .

Решение этой задачи во многих случаях приведено в табличной форме в зависимости от конструкции фундаментов (Справочник проектировщика).

;

Расчет балок по методу общих упругих деформаций.

(Гипотеза упругого полупространства)

; где Г — гибкость балки;

l — полудлина балки;

h – высота балки;

Е – модуль упругости материала балки;

Е₀ – модуль общей деформации грунта.

Г 10 — жёсткая балка (метод Горбунова-Посадова)

Г>10 — гибкая балка

Часто при расчете гибких фундаментов (особенно если жесткость балки применима)- переходят к решению задач по методу Жемочкина Б.Н. (Исследование приемов строительной механики для решения статически неопределимых систем).

Метод Жемочника для расчета фундаментных балок

на упругом основании.

В 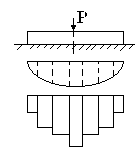основу метода положены следующие допущения:

Действительная криволинейная эпюра

распределения давлений под подошвой

балки заменяется ступенчатой

Распределение давлений на ширине балки

также принимаются равномерным.

Между балкой и сжимаемым основанием предполагаются жесткие шарниры опирающиеся стержни, воспринимающие усилия от балки и равномерно распределяющие это усилие на основание.

4. Условие совместимости работы балки и основания и удовлетворяются равенством прогиба балки и осадки основания в месте закрепления опорного стержня y_i=S_i .

Этот метод является универсальным и позволяет решать любые задачи с любой степенью сложности.

Составляется система канонических уравнений (строительная механика):

Задача решается смешанным методом.

— единичное перемещение по направлению «к» связи от воздействия «i» связи

— единичное перемещение, вызванное осадкой основания

— единичное перемещение, вызванное прогибом балки

; -находятся обычно по таблицам

Решив систему уравнений и найдя Xi, определяют величины реактивных давлений Рi, соответствующих ширине принятых участков ступенчатой эпюры (см. допущение № 1):

Затем с использованием метода сечений строят эпюры изгибающих моментов M, а по ним окончательно определяют сечение балки и ее армирование

Источник