Как распределяется напряжение в основании. Определение несущей способности основания
Чтобы рассчитать осадку фундамента и проверить прочность (несущую способность) основания, нужно знать распределение напряжений в основании, т. е. его напряженное состояние. Необходимо иметь сведения о распределении напряжений не только по подошве фундамента, но и ниже нее, так как осадка фундамента является следствием деформации толщи грунта, расположенной под ним. Для расчета несущей способности основания также приходится определять напряжения в грунте ниже подошвы фундамента. Без этого нельзя установить наличие и размеры областей сдвигов, проверить прочность прослойки слабого грунта и т. д.
Для теоретического определения напряжений в основании используют, как правило, решения теории упругости, полученные для линейно деформируемого однородного тела. В действительности грунт не является ни линейно деформируемым, телом, так как деформации его не прямо пропорциональны давлению, ни однородным телом, так как плотность его меняется с глубиной. Однако эти два обстоятельства не сказываются существенно на распределении напряжений в основании.
В данной главе рассматриваются не все вопросы напряженного состояния оснований, а только методика определения нормальных напряжений, действующих в грунте по горизонтальным площадкам.
Распределение напряжений по подошве фундамента
В мостовом и гидротехническом строительстве, как правило, применяют жесткие фундаменты, деформациями которых можно пренебречь, поскольку они малы по сравнению с перемещениями, связанными с осадкой.
Измерения нормальных напряжений (давлений) по подошве фундамента, выполненные с помощью специальных приборов, вмонтированных на уровне подошвы, показали, что эти напряжения распределены по криволинейному закону, зависящему от формы и размеров фундамента в плане, свойств грунта, среднего давления на основание и других факторов.
Рис. 2.1. Фактическая и теоретическая эпюры нормальных напряжений по подошве фундамента
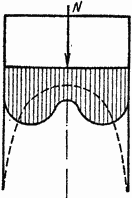
В качестве примера на рис. 2.1 сплошной линией показано фактическое распределение нормальных напряжений (эпюра нормальных напряжений) по подошве фундамента, когда нагрузка (сила N) значительно меньше несущей способности основания, а пунктиром — распределение напряжений, полученное на основе решений теории упругости.
В настоящее время, несмотря на накопленный экспериментальный материал и теоретические исследования, не представляется возможным устанавливать в каждом конкретном случае действительное распределение давлений по подошве фундамента. В связи с этим в практических расчетах исходят из прямолинейных эпюр давлений.
Рис. 2.2. Прямолинейные эпюры нормальных напряжений по подошве фундамента а — при центральном сжатии; б— при внецентренном сжатии и e W/A
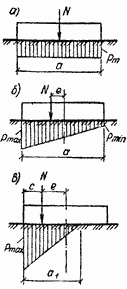
Рис. 2.2. Прямолинейные эпюры нормальных напряжений по подошве фундамента а — при центральном сжатии; б— при внецентренном сжатии и e W/AПри центральном сжатии (рис. 2.2, а) напряжения Pm, кПа, по подошве принимают равномерно распределенными и равными:
Pm = N/A, (2.1)
где N — нормальная сила в сечении по подошве фундамента, кН; А — площадь подошвы фундамента, м 2 .
При внецентренном сжатии эпюру напряжений принимают в виде трапеции (рис. 2.2, б) или треугольника (рис. 2.2, в). В первом из этих случаев наибольшее ртах и наименьшее Pmin напряжения определяются выражениями:
Pmax = N/A + M/W;
Pmin = N/A – M/W (2.2)
где M — Ne — изгибающий момент в сечении по подошве фундамента, кН·м (здесь е — эксцентриситет приложения силы N, м); W — момент сопротивления площади подошвы фундамента, м 3 .
Формулы (2.2) справедливы в случаях, когда изгибающий момент действует в вертикальной плоскости, проходящей через главную центральную ось инерции подошвы фундамента.
При подошве фундамента в виде прямоугольника с размером, перпендикулярным плоскости действия момента М, b и другим размером a имеем A = ab и W = ba2/6. Подставляя выражения A и W в формулы (2.2) и учитывая, что M = Ne, получаем:
Pmax =N/ba(1+6e/a)
Pmin=N/ba(1-6e/a) (2.3)
Напряжение Pmin, кПа, вычисленное по формуле (2.2) или (2.3) при эксцентриситете e> W/A, получается отрицательным (растягивающим). Между тем в сечении по подошве фундамента таких напряжений практически быть не может. При е> W/A край подошвы фундамента, более удаленный от силы N, поднимается под действием этой силы над грунтом. На некотором участке подошвы фундамента (со стороны этого края) контакт между фундаментом и грунтом нарушается (происходит так называемое отлипание фундамента от грунта), а потому эпюра напряжений P имеет вид треугольника (см. рис. 2.2, в). Этого обстоятельства формулы (2.2) и (2.3) не учитывают, поэтому ими нельзя пользоваться при е> W/A.
Формулы для определения размера а1, м, части подошвы, по которой сохраняется контакт фундамента с грунтом, и наибольшего напряжения Pmax, кПа (см. рис. 2.2, в), можно получить, если учесть, что напряжения P должны уравновесить силу N, кН, действующую на расстоянии с от ближайшего к этой силе края подошвы фундамента.
Отсюда вытекают два условия: 1) центр тяжести эпюры напряжений P расположен на линии действия силы N; 2) объем эпюры равен величине этой силы. Из первого условия при прямоугольной подошве фундамента следует
А1=3с, (2.4)
а из второго
(Pmax а1/2)b = N. (2.5)
Из формул (2.4) и (2.5) получаем
Pmax =2N/(3cb). (2.6)
Итак, при эксцентриситете е> W/A = a/6 наибольшее давление по прямоугольной подошве фундамента Pmax следует определять по формуле (2.6).
Источник
5.5.3. Определение основных размеров фундаментов (ч. 1)
Основные размеры фундаментов мелкого заложения (глубина и размеры подошвы) в большинстве случаев определяются исходя из расчета оснований по деформациям, который включает:
- – подсчет нагрузок на фундамент;
- – оценку инженерно-геологических и гидрогеологических условий площадки строительства; определение нормативных и расчетных значений характеристик грунтов;
- – выбор глубины заложения фундамента;
- – назначение предварительных размеров подошвы по конструктивным соображениям или исходя из условия, чтобы среднее давление на основание равнялось расчетному сопротивлению грунта, приведенному в табл. 5.13;
- – вычисление расчетного сопротивления грунта основания R по формуле (5.29), изменение в случае необходимости размеров фундамента с тем, чтобы обеспечивалось условие p ≤ R ; в случае внецентренной нагрузки на фундамент, кроме того, проверку краевых давлений;
- – при наличии слабого подстилающего слоя проверку соблюдения условия (5.35);
- – вычисление осадок основания и проверку соблюдения неравенства (5.28); при необходимости корректировку размеров фундаментов.
В случаях, оговоренных в п. 5.1, выполняется расчет основания по несущей способности. После этого производятся расчет и конструирование самого фундамента.
А. ЦЕНТРАЛЬНО НАГРУЖЕННЫЕ ФУНДАМЕНТЫ
Определение размеров подошвы фундамента по заданному значению расчетного сопротивления грунта основания. Обычно вертикальная нагрузка на фундамент N0 задается на уровне его обреза, который чаще всего практически совпадает с отметкой планировки. Тогда суммарное давление на основание на уровне подошвы фундамента будет:
где 
— среднее значение удельного веса фундамента и грунта на его обрезах, принимаемое обычно равным 20 кН/м 3 ; d и А — глубина заложения и площадь подошвы фундамента.
Если принять p = R , получим следующую формулу для определения необходимой площади подошвы фундамента:
Задавшись соотношением сторон подошвы фундамента η = l/b , получим:
Зная размеры фундамента, вычисляют его объем и вес Nf , а также вес грунта на его обрезах Ng и проверяют давление по подошве:
Определение размеров подошвы фундамента при неизвестном значении расчетного сопротивления грунта основания. Как видно из формулы (5.29), расчетное сопротивление грунта основания зависит от неизвестных при проектировании размеров фундамента (глубины его заложения d и размеров в плане b×l ), поэтому обычно эти размеры определяются методом последовательных приближений. В качестве первого приближения принимают размеры фундамента по конструктивным соображениям или из условия (5.41), т.е. принимая R = R0 .
Однако необходимые размеры подошвы фундамента можно определить за один прием. Из формулы (5.41)
ηb 2 (R – d) – N0 = 0 ,
а с учетом формулы (5.29) при b kz = 1)
Уравнение (5.43) приводится к виду:
для ленточного фундамента
для прямоугольного фундамента
;
;
Решение квадратного уравнения (5.44) производится обычным способом, а уравнения (5.45) — методом последовательного приближения или по стандартной программе.
После вычисления значения b с учетом модульности и унификации конструкций принимают размеры фундамента и проверяют давление по его подошве по формуле (5.42).
Пример 5.7. Определить ширину ленточного фундамента здания жесткой конструктивной схемы без подвала ( db = 0). Отношение L/H = 1,5. Глубина заложения фундамента d = 2 м. Нагрузка на фундамент на уровне планировки n0 = 900 кН/м. Грунт — глина с характеристиками, полученными при непосредственных испытаниях: φII = 18°, cII = 40 кПа, γII = γ´II = 18 кН/м 3 , IL = 0,45.
Решение. по табл. 5.10 имеем: γс1 = 1,2 и γс2 = 1,1; по табл. 5.11 при φII = 18°; Мγ = 0,43; Мq = 2,73; Мc = 5,31. Поскольку характеристики грунта приняты по испытаниям, k = 1.
Для определения ширины фундамента b предварительно вычисляем:
;
a1 = 1,2·1,1(2,73 · 2 · 18 + 5,31 · 40) – 20 · 2 = 370,1.
Подставляя эти значения в формулу (5.44), получаем 10,22 b 2 + 370,1 b – 900 = 0, откуда
м.
Принимаем b = 2,4 м.
Пример 5.8. Определить размеры столбчатого фундамента здания гибкой конструктивной схемы ( γс2 = 1). Соотношение сторон фундамента η = l/b = 1,5, нагрузка на него составляет: N0 = 4 МН = 4000 кН. Грунтовые условия и глубина заложения те же, что и в предыдущем примере.
a0η = 1,2 · 1 · 0,43 · 18 · 1,5 = 13,93;
a1η = [1,2 · 1(2,73 · 2 · 18 + 5,31 · 40) – 20 · 2] 1,5 = 499,22.
Затем, подставляя в уравнение (5.45) полученные величины (13,93 b 3 + 499,22 b 2 – 4000 = 0) и решая его по стандартной программе, находим b = 2,46 м, тогда l = 1,5 b = 3,7 м.
Принимаем фундамент с размерами подошвы 2,5×3,7 м.
Определение размеров подошвы фундамента при наличии слабого подстилающего слоя. При наличии в пределах сжимаемой толщи основания (на глубине z от подошвы фундамента) слоя грунта с худшими прочностными свойствами, чем у лежащего выше грунта, размеры фундамента необходимо назначать такими, чтобы обеспечивалось условие (5.35). Это условие сводится к определению суммарного вертикального напряжения от внешней нагрузки и от собственного веса лежащих выше слоев грунта ( σz = σzp + σzg ) и сравнению этого напряжения с расчетным сопротивлением слабого подстилающего грунта R применительно к условному фундаменту, подошва которого расположена на кровле слабого грунта.
Пример 5.9. Определить размеры столбчатого фундамента при следующих инженерно-геологических условиях (см. рис. 5.24). На площадке от поверхности до глубины 3,8 м залегают песни крупные средней плотности маловлажные, подстилаемые суглинками. Характеристики грунтов по данным испытаний: для песка φII = 38°, сII = 0, γII = γ´II = 18 кН/м 3 , E = 40 МПа; для суглинков φII = 19°, сII = 11 кПа, γII = 17 кН/м 3 , E = 17 МПа. Здание — с гибкой конструктивной схемой без подвала ( db = 0). Вертикальная нагрузка на фундамент на уровне поверхности грунта N0 = 4,7 MH. Глубина заложения фундамента d = 2 м. Предварительные размеры подошвы фундамента примяты исходя из R = 300 кПа (табл. 5.13) равными 3×3 м.
Решение. по формуле (5.29) с учетом табл. 5.11 и 5.12 получаем;
кПа.
Для определения дополнительного вертикального напряжения от внешней нагрузки на кровле слабого грунта предварительно находим:
среднее давление под подошвой
p = N0/b 2 + d = 4,7 · 10 3 /3 2 + 20 · 2 = 520 + 40 = 560 кПа;
дополнительное давление на уровне подошвы
По табл. 5.4 при ζ = 2z/b = 2 · 1,8/3 = 1,2 коэффициент α = 0,606. Тогда дополнительное вертикальное напряжение па кровле слабого слоя от нагрузки на фундамент будет:
Ширина условного фундамента составит:
м.
Для условного фундамента на глубине z = 1,8 м при γc1 = γc2 = k = 1 расчетное сопротивление суглинков по формуле (5.29) будет:
Rz = 0,47 · 4 · 17 + 2,88 · 3,8 · 18 + 5,48 · 11 = 30 + 196 + 60 = 286 кПа.
Вертикальное нормальное напряжение от собственного веса грунта на глубине z = 3,8 м
Проверяем условие (5.35):
315 + 62 = 377 > Rz = 286 кПа,
т.е. условие (5.35) не удовлетворяется и требуется увеличить размеры фундамента. Расчет показал, что в данном случае необходимо принять b = 3,9 м.
Сорочан Е.А. Основания, фундаменты и подземные сооружения
Источник