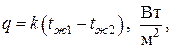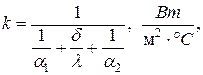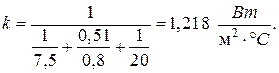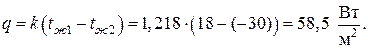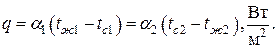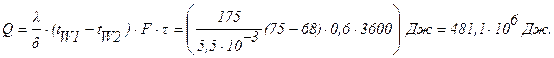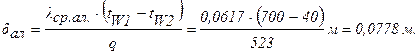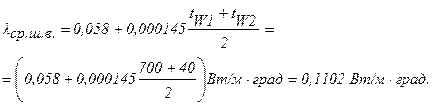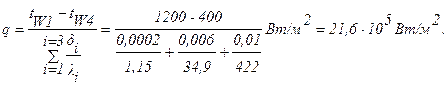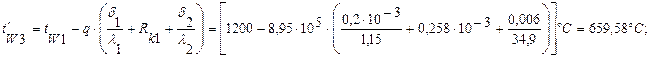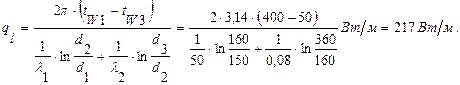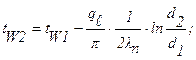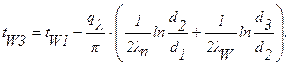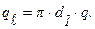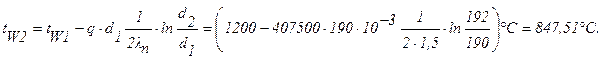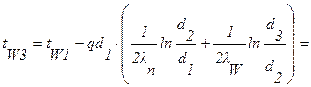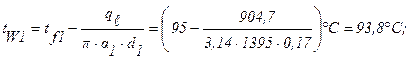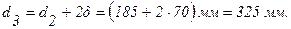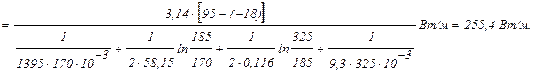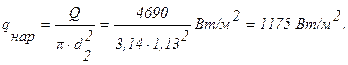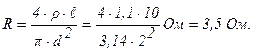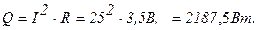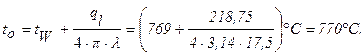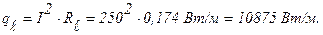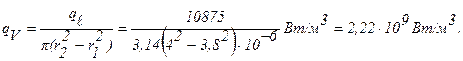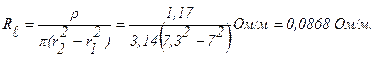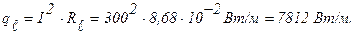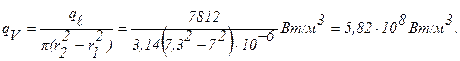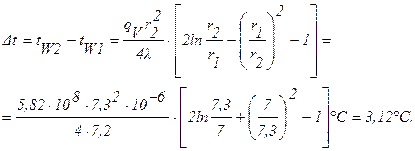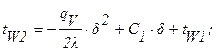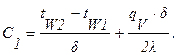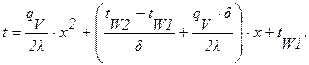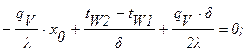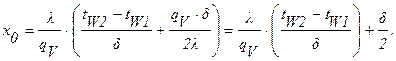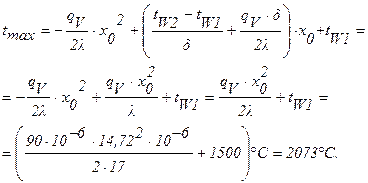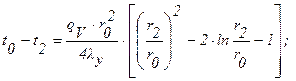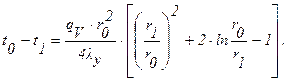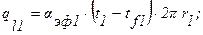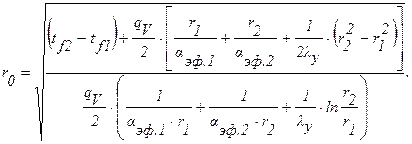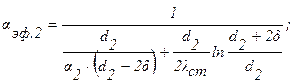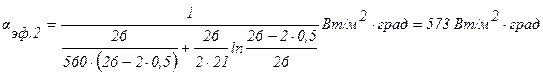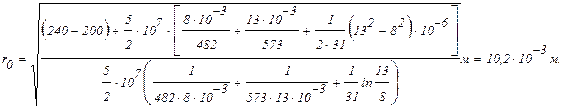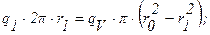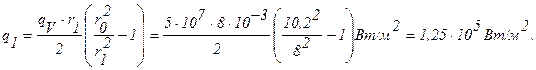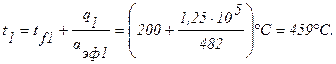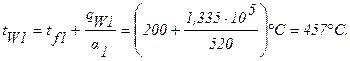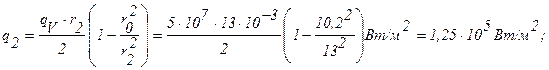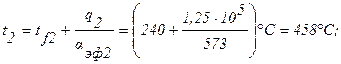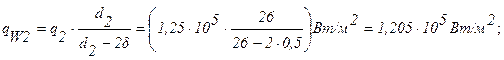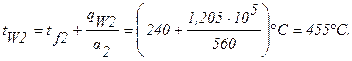Найти тепловой поток через стену

Расчет коэффициентов теплопередачи онлайн

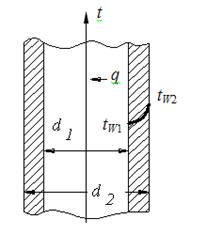
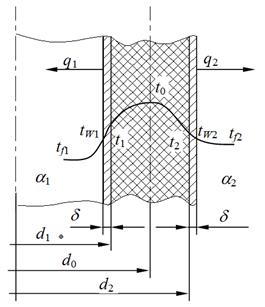
При расчете теплообменных аппаратов, анализе теплового баланса работающего оборудования, оценке тепловых потерь ирешении многих других задач теплообмена, часто необходимо рассчитать тепловой поток, проходящий через твердую стенку, разделяющую жидкости или газы при различных температурах, который в простейшем случае вычисляется по формуле:

K — коэффициент теплопередачи;

T_f1 , T_f2 — температуры жидкости или газа между которыми происходит теплообмен

Как видно, наибольшую сложность здесь представляет определение коэффициента теплопередачи k, который зависит от физических свойств теплоносителя, режима течения и коэффициента теплопроводности твердой стенки. Коэффициент теплопередачи плоской стенки можно выразить через коэффициенты теплоотдачи поверхностей стенки:

α₁ , α₂ — коэффициенты теплоотдачи поверхностей стенки;

λ — коэффициент теплопроводности стенки;

δ — толщина стенки;

Вычислив коэффициенты теплоотдачи, на данной странице можно рассчитать тепловой поток, передаваемую мощность, коэффициент теплопередачи и температуру плоской или цилиндрической стенки.

Расчет теплопередачи через плоскую стенку

Исходные данные:

H — толщина стенки, миллиметрах;

S — площадь стенки, метрах 2 ;

T_fa — температура среды А, в °C;

α_a — коэффициент теплоотдачи поверхности А, в ватт/метр 2 ×°C;

T_fb — температура среды B, в °C;

α_b — коэффициент теплоотдачи поверхности B, в ватт/метр 2 ×°C.

ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ

Толщина стенки, H, мм

Площадь стенки, S, м 2

Теплопроводность стенки λ, Вт/(м* 0 C×сек)

Температура среды А, Т_fа, 0 С

Коэффициент теплоотдачи, α_а, Вт/м 2 * 0 С

Температура среды B, Т_fb, 0 С

Коэффициент теплоотдачи, α_b, Вт/м 2 * 0 С

Источник

Задача №1.17

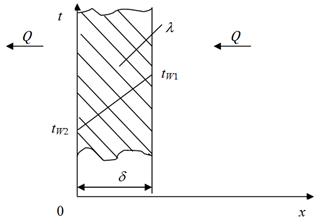
Определить тепловой поток через 1м 2 кирпичной стены помещения толщиной в два кирпича (δ= 510 мм) с коэффициентом теплопроводности λ=0,8 Вт/(м ºС). Температура воздуха внутри помещения t_ж1 = 18°C; коэффициент теплоотдачи к внутренней поверхности стенки α₁=7,5Вт/(м 2º С); температура наружного воздуха t_ж2 = -30°C; коэффициент теплоотдачи от наружной поверхности стены, обдуваемой ветром, α₂=20Вт/(м 2º С). Вычислить также температуры на поверхностях стены t_с1 и t_с2.

Дано: δ= 510мм; λ =0,8 Вт/(м∙ º С); α1 =7,5 Вт/(м 2 ∙ º С); α2 =20 Вт/(м 2 ∙ º С); tж1 = 18 °C; tж2 = -30 °C; Найти: рассчитать плотность теплового потока, 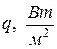; определить температуру tc1 и tc2

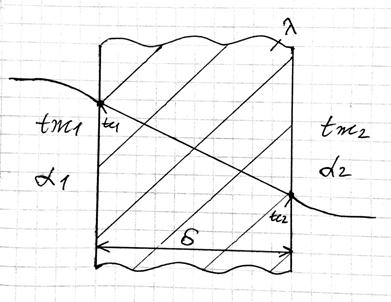Решение

1. Согласно уравнению теплопередачи через плоскую стенку, плотность теплового потока вычисляется:

где 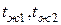-температура воздуха внутри помещения и снаружи соответственно, ˚С; k — коэффициент теплопередачи, который характеризует интенсивность теплопередачи, и численно равен плотности теплового потока, передающейся от первой жидкости (воздуха внутри помещения) к другой (воздуху снаружи помещения) через разделяющую их стенку при разности температур между жидкостями в 1 ˚С, Вт/(м 2 ∙ º С).

Коэффициент теплопередачи определяется следующим образом:

где 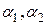-коэффициент теплоотдачи к внутренней поверхности и от наружной поверхности обдуваемой ветром соответственно, этот коэффициент характеризует интенсивность теплоотдачи и численно равен плотности теплового потока, передаваемого при разности температур равной 1 ˚С, Вт/(м 2 ∙ º С).

Значит плотность теплового потока:

2. Согласно закону Ньютона – Рихмана:

Из этого соотношения и определим температуры стенок t_c1 и t_c2.

Источник

Найти тепловой поток через стену

Чтобы понять, как считать теплопроводность — необходимо представить материал в виде вымышленной стены. На практике такие стены будут реальными. Данная статья поможет нам рассчитать теплопотери стены. Сложив все теплопотери стен — получим теплопотери всего дома. Но это только один фактор из трех составляющих теплопотерь дома. Не забывайте про вентиляцию и излучение тепла. О них поговорим в других статьях.

t₁, t₂ — точки температур. L — толщина стены. S — площадь стены.

Теплопроводность представляет собой количество теплоты, которое проходит в единицу времени через единицу толщины слоя материала.

Если быть точнее! То это отношение поверхностной плотности теплового потока к температурному градиенту.

Температурный градиент — это произведение толщины стенки материала на разность температур между противоположными плоскостями одной стенки.

Температурный градиент = L х ( t₁ — t₂ ).

Плотность теплового потока — это количество теплоты в единицу времени. Количество теплоты измеряется в Калориях. О калориях поговорим ниже.

Сначала я Вам покажу формулу нахождения теплопроводности и связи между ними.

λ — Коэффициент теплопроводности.

t₁,t₂ — температуры стенки по разные стороны. Измеряется либо в Цельсиях [°C] либо в Кельвинах [K].

[ Вт / (м•°С) ] либо [ Вт / (м•K) ]

В редких случаях за место (Вт) может использоваться (Калория).

L — Толщина стенки, измеряется в метрах(м).

Q — Количество теплоты, измеряется в калориях(K) или в ваттах(Вт).

Эталоном значения одной калории является: Количество теплоты необходимое для того, чтобы нагреть один грамм воды на 1 градус Цельсия или Кельвина, при атмосферном давлении (101325 Па).

1 Дж = 0,2388 калорий 1000 Калорий = 1 кКалория = 1,163 Ватт • час 1 Калория = 4,1868 Дж

Для глубокого понимания коэффициента теплопроводности, нужно понимать, как находят количество теплоты. То есть нам нужно найти количество теплоты, которое расходуется между наружными плоскостями одной стены. Мы фактически находим потерянное тепло через стену.

Данная формула помогает нам найти проходящее количество теплоты в сквозь стену.

Также еще выражаются в такой форме:

R — Температурное сопротивление, измеряется: (м 2 • °С) / Вт, или: (м 2 • K) / Вт

Q — Количество теплоты. Измеряется в Ваттах (Вт) или Калориях (К)

t₁,t₂ — температура стенки по разные стороны. Измеряется либо в Цельсиях [°C] либо в Кельвинах [K].

S — площадь стенки, измеряется в квадратных метрах (м 2 ). Площадь находится умножением высоты на длину стенки. S = a • b.

Чем больше значение λ, тем большей теплопроводностью обладает вещество. В общем случае теплопроводность для данного вещества не является величиной постоянной: для твердых тел λ зависит от температуры, а для жидких и газообразных — еще и от давления.

Для металлов (кроме алюминия) теплопроводность с увеличением температуры несколько убывает, что означает, что холодный металл проводит теплоту лучше, чем нагретый. Теплопроводность металлов λ составляет 2,3-420 Вт/(м•К).

Для изоляционных и огнеупорных материалов λ при повышении температуры возрастает. Последнее объясняется тем, что большинство изоляционных материалов не представляют монолитной массы, а являются пористыми телами — конгломератом отдельных частиц с воздушными прослойками между ними. Эти воздушные прослойки уменьшают теплопроводность, но лучистый теплообмен, происходящий в этих прослойках, в итоге увеличивает суммарный теплоперенос при повышении температуры пористого тела. Для таких материалов λ зависит не только от свойств собственно материала, но и от степени его уплотнения, т.е. от плотности. Кроме того, на теплопроводность указанных материалов большое влияние оказывает влажность. С увеличением влажности теплопроводность возрастает. Для влажного материала λ выше, чем для сухого материала и воды, взятых в отдельности. Так, например, для сухого кирпича λ = 0,35 Вт/(м•К), для воды λ = 0,58 Вт/(м•К), а для влажного кирпича λ = 1,05 Вт/(м•К). Это объясняется тем, что адсорбированная в капиллярно-пористых телах вода отличается по физическим свойствам от свободной воды. Поэтому по отношению к такого рода веществам правильнее говорить о так называемой видимой теплопроводности. Теплопроводность теплоизоляционных материалов составляет 0,02—3,0 Вт/(м•К).

Для газов с увеличением температуры теплопроводность также возрастает, но от давления λ практически не зависит, кроме очень низких (менее 2,5 кПа) и очень высоких (более 200 МПа) давлений. Теплопроводность газов колеблется от 0,006 до 0,6 Вт/(м•К).

Для большинства капельных жидкостей теплопроводность находится в пределах 0,09—0,7 Вт/(м•К) и с повышением температуры уменьшается. Вода является исключением: с ростом температуры от 0 до 150 °С теплопроводность возрастает, а при дальнейшем увеличении температуры уменьшается.

У меня дома в квартире, в комнате имеется наружная не утепленная стена площадью ( 2,5 х 5метров ), зимой очень холодно. Температура стены 20 °C. Стена без окна. Определить сколько уходит тепла через стену на улицу зимой, когда на улице температура -30 градусов. Стена кирпичная. Толщина 80 см.

S=2,5 х 5 = 12,5 м 2

t1 = 20 °C, K1 = t1 + 273,15 = 293,15

t2 = -30 °C, K2 = t1 + 273,15 = 243,15

L = 80см = 0,8 метров.

Для кирпича из других источников:

λ = 0,44 Вт/(м•К) в переводе на Цельсия: = 0,44 Вт/(м•°С)

Решение простое: Просто вставляем в формулу имеющиеся значения и занимаемся арифметикой.

Q = 0,44 х (20-(-30))/0,8 х 12,5 = 0,44 х 50/0,8 х 12,5 = 343,75 Вт

Ответ: Теряется тепло стены на 344 Вт.

Если посчитать за месяц, то это будет: 344 Вт х 24 часа х 30 дней = 247,7 кВт•ч.

И это одна только стена столько потребляет! А сколько таких стен может быть?

Конечно, точность расчетов зависит от значения коэффициента теплопроводности для материала, из которого сделана стена. Влажность, тоже имеет значение. Так что этих коэффициентов в инете полным-полно, можете подобрать из различных таблиц.

В целом такой расчет очень даже полезный и почти совпадает с реальными цифрами.

Таблицы я позже приготовлю! В других статьях будут. А так продолжение следует.

Источник

Задача № 1 — Контрольная работа по дисциплине «Основы энергосбережения»

Определить тепловой поток через стены здания общей поверхностью F (м²) для трех вариантов:

1. Стена бетонная, толщиной δ = 300мм, коэффициент теплопроводности λб = 1 .

2. Стена кирпичная, толщиной δ = 300 мм, коэффициент теплопроводности λк = 0,7 .

3. Стена кирпичная, между двумя слоями кирпичной кладки с толщиной каждого слоя δ = 150 мм, установлена прокладка пенопласта толщиной δп = 50 мм с коэффициентом теплопроводности λп = 0,05 .

Температуры на внутренней и внешней поверхностях стен соответственно равны tвн и tн . Рассчитать снижение потерь тепла через стены эдания по сравнению с комбинированной стеной и определить экономию условного топлива, если продолжительность отопительного сезона τ = 4600 часов. Данные для решения задачи выбрать из таблицы 1.

F = 5000 м², tвн = 14°C, tн = -15°C.

1. Определим термическое сопротивление стен и тепловой поток через стены здания для трех вариантов по следующему выражению:

Вариант 1: Rб=0,3/1=0,3 (м2*град/Вт);

Вариант 2: Rк=0,3/0,7=0,43 (м2*град/Вт);

Вариант 3: Rкомб=(2*0,15/0,7)+0,05/0,05=1,43 (м2*град/Вт).

2. Рассчитаем тепловой поток через плоские поверхности для трех вариантов по следующему выражению:

Q = tвн – tн / t=1nRi * F * 10-3 (кВт),

где Ri = δi / λi – термическое сопротивление плоской стенки (м2*град/Вт);

Вариант 1: Qб=29/0,3*5000*10-3=483,33 (кВт);

Вариант 2: Qк=29/0,43*5000*10-3=337,2 (кВт);

Вариант 3: Qкомб=29/1,43*5000*10-3=101,39 (кВт).

3. Определим расход условного топлива на отопление здания по формуле:

где Qн.у.т=29300 (кДж/кг) – теплота сгорания условного топлива.

Вариант 1: Ву.т.=483/29300*3600=59,38 (кг/ч);

Вариант 2: Ву.т.=337,2/29300*3600=41,43 (кг/ч);

Вариант 3: Ву.т.=101,39/29300*3600=12,45 (кг/ч).

4. Определим расход топлива в сезон по формуле:

Вариант 1: Вгод.= 59,38*4600=273148 (кг);

Вариант 2: Вгод=41,43*4600=190578 (кг);

Вариант 3: Вгод=12,45 * 4600=57270(кг).

5. Сравнить экономию между вариантами:

Экономия в сравнении 1 и 2 вариантов:∆в1-2=273148-190578=82570 кг;

Экономия в сравнении 2 и 3 вариантов:∆в2-3=190578-57270=133308 кг;

Экономия в сравнении 1 и 3 вариантов:∆в1-3=273148-57270=215878 кг.

Ответ: При выборе комбинированных стен зданий вместо кирпичных экономия условного топлива за отопительный сезон составит 133308 кг, а при выборе комбинированных стен вместо бетонных экономия условного топлива за отопительный сезон составит 215878 кг.

Поможем написать любую работу на аналогичную тему

Источник

Примеры решения задач по теплопроводности.

Задача 1. Определить количество теплоты, которое передается в течение 1 часа через стенки картера авиадвигателя, если толщина стенок d = 5,5 мм, площадь поверхности стенок F = 0,6 м 2 , температура на внутренней поверхности картера t_W1= 75°С, на наружной t_W2= 68°С, а средний коэффициент теплопроводности стенок

Решение : Количество теплоты, передаваемое через стенки картера в течение 1 часа, будет равно:

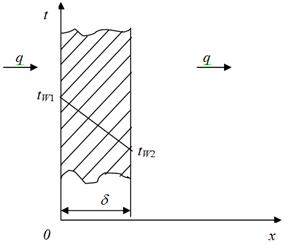
Задача 2. Вычислить плотность теплового потока через плоскую однородную стенку(l — коэффициент теплопроводности), толщина которой значительно меньше ширины и высоты, если стенка выполнена:

а) из стали (l= 40 Вт/м×град);

б) из бетона (l= 1,1 Вт/м×град);

в) из кирпича (l= 0,11 Вт/м×град).

Во всех трех случаях толщина стенки d =50 мм. Температуры на поверхностях стенки поддерживаются постоянными и равными t_W1=100°С и t_W2=90°С.

Решение: Плотность теплового потока q определяется выражением (1.6):

.

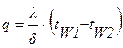
для стенки из стали ;

для стенки из бетона ;

для стенки из кирпича .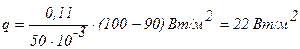

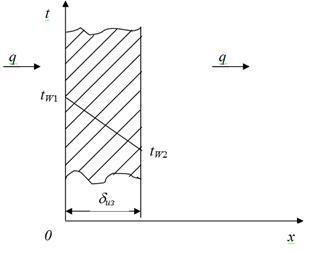
Задача 3. Определить толщину тепловой изоляции d, выполненной из:

2) шлаковой ваты.

Удельные потери теплоты через изоляционный слой q =523 Вт/м 2 , температуры его поверхности t_W1=700°C и t_W2=40°C. Коэффициент теплопроводности альфоля l= 0,0302+0,000085×t и коэффициент теплопроводности шлаковой ваты
l= 0,058+0,000145×t. Здесь t – средняя температура изоляции в °C.

Решение: В случае линейной зависимости коэффициента теплопроводности от температуры плотность теплового потока определяется по формуле для постоянного коэффициента теплопроводности, взятого при средней температуре стенки /20, задача 1-6/, т.е.:

Определяем толщину альфолиевой изоляции:

Определяем l_ср шлаковой ваты:

Толщина тепловой изоляции из шлаковой ваты:

.

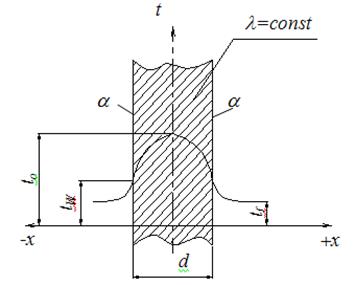
Задача 4. Плоская стенка (коэффициент теплопроводности l = 11,6 Вт/м×град, толщина d = 0,005 м) омывается с одной стороны горячими газами с температурой

t_f1 = 2000°С, а с другой стороны охлаждается водой с t_f2 = 27°С. Коэффициенты теплоотдачи от газа к стенке a₁ = 467 Вт/м 2 ×град, от стенки к воде
a₂ = 3500 Вт/м 2 ×град. Определить удельный тепловой поток и температуры стенки t_W1, t_W2.

Решение : Удельный тепловой поток через стенку равен (формула 1.12):

.

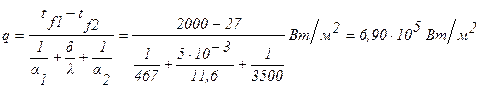
Температуры стенок определяются (формулы 1.10, 1.11):

;

.

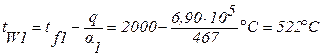
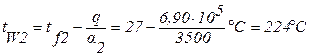
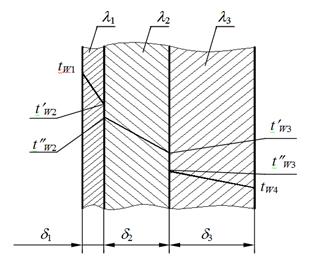
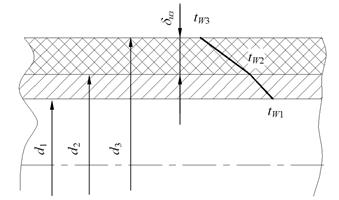
Задача 5. Определить удельный тепловой поток с учетом и без учета теплового сопротивления контакта через многослойную плоскую стенку, состоящую из слоя окиси циркония толщиной d₁ = 0,2 мм, слоя стали толщиной d₂ = 6 мм, слоя алюминия толщиной d₃=10мм, если температуры на внешних поверхностях стенки поддерживаются постоянными и равными t_W1 = 1200°С и t_W4 = 400°С; коэффициент теплопроводности окиси циркония l₁ = 1,15 Вт/м×град, стали l₂ = 34,9 Вт/м×град и алюминия l₃ = 422 Вт/м×град. Термическое сопротивление контакта между слоями окиси циркония и стали R_к1 = 0,258×10 -3 м 2 град/Вт, а между слоями стали и алюминия R_к2 = 0,266×10 -3 м 2 град/Вт. Определить температуры на контактирующих поверхностях каждого слоя.

Решение: Для трехслойной стенки при стационарной теплопроводности с учетом теплового сопротивления контакта удельный тепловой поток определяется выражением (формула 1.9 для n-слойной стенки):

.

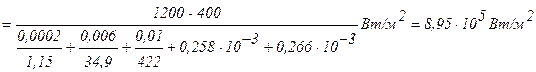
Для трехслойной стенки без учета теплового сопротивления удельный тепловой поток определяется формулой (1.7), т.е.:

Температуры на контактирующих поверхностях будут равны:

Задача 6. Змеевики пароперегревателя выполнены из труб жаропрочной стали диаметром d₁/d₂=32/42 мм с коэффициентом теплопроводности l=14 Вт/м×град. Температура внешней поверхности трубы t_W2=580°С, внутренней – t_W1=450°С. Вычислить удельный тепловой поток через стенку на единицу длины трубы.

Решение: Поток тепла, проходящий через единицу трубы, представляющей собой цилиндрическую стенку, равен (формула 1.18):

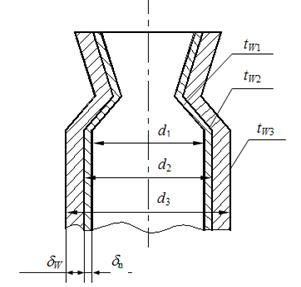
Задача 7. Паропровод диаметром 150/160 мм покрыт слоем тепловой изоляции толщиной d_из=100мм. Коэффициенты теплопроводности стенок трубы

l₁=50 Вт/м×град и изоляции l₂=0,08 Вт/м×град. Температура на внутренней поверхности паропровода t_W1=400°С и на наружной поверхности изоляции t_W3=50°С. Найти тепловые потери с 1 м паропровода и температуру на границе соприкосновения паропровода и изоляции t_W2.

Решение: Внешний диаметр паропровода равен:

.

Тепловые потери с 1м паропровода будут равны (формула 1.19):

Температура t_W2 будет равна (из формулы 1.18):

Задача 8. Определить температуры на поверхности соприкосновения слоев стенки t_W2 камеры сгорания жидкостного ракетного двигателя и на внешней поверхности t_W3, если диаметр камеры d₁=190 мм, толщина защитного покрытия d_n=1 мм и его коэффициент теплопроводности l_n=1,15 Вт/м×град, а толщина основной стенки

d_W=2 мм и ее коэффициент теплопроводности l_W=372 Вт/м×град. Удельный тепловой поток q=407500 Вт/м 2 , температура на поверхности покрытия со стороны камеры t_W1=1200°С.

Решение: Из формул (1.18) и (1.19) будем иметь:

Из условий задачи:

;

;

.

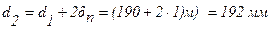
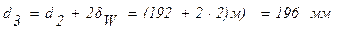
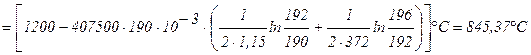
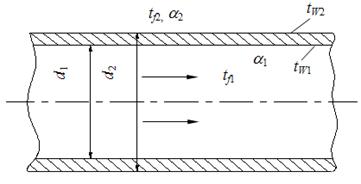
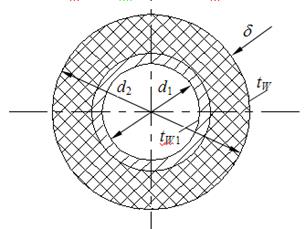
Задача 9. По неизолированному трубопроводу диаметром 170/185 мм, проложенному на открытом воздухе, протекает вода со средней температурой t_f1= 95°С, температура окружающего воздуха t_f2= -18°С. Определить потерю теплоты с 1м длины трубопровода и температуры на внутренней и внешней поверхностях этого трубопровода, если коэффициент теплопроводности материала трубы

l=58,15 Вт/м×град, коэффициент теплоотдачи от воды к стенке трубы
a₁=1395 Вт/м×град и от трубы к окружающему воздуху
a₂= 13,95 Вт/м×град.

Решение: Потеря тепла с 1м длины трубопровода будет равна (формула 1.21):

Температуры на внутренней и внешней поверхностях практически равны (формулы для определения температур аналогичны выражениям (1.10), (1.11) для плоской стенки):

Задача 10. Определить тепловые потери на 1м длины трубопровода, а также температуры на внутренней и внешней поверхностях при условии, что трубопровод, рассматриваемый в задаче 1.9, покрыт слоем изоляции толщиной d =70 мм с коэффициентом теплопроводности l_из= 0,116 Вт/м×град, а коэффициент теплоотдачи поверхности изоляции к окружающей среде a₂=9,3 Вт/м 2 ×град. Остальные условия те же, что и в задаче 1.9.

Решение: В соответствии с условиями задачи

Тепловые потери на 1 м длины трубопровода можно определить по формуле (1.22):

Температуры на поверхностях трубопровода будут равны:

Задача 11. Шаровой реактор, внутренний диаметр которого d₁ = 1м, имеет общую толщину стенки и слоя изоляции d = 65мм с эквивалентным коэффициентом теплопроводности l_экв = 1,047 Вт/м×град. Определить удельную тепловую нагрузку внутренней и наружной поверхностей стенки реактора, если температура внутренней поверхности стенки t_W1 = 160°С, а внешней t_W2= 60°С.

Решение: Из условий задачи: d₂= d₁ +2d =(1000+2×65) мм=1130 мм.

Общее количество теплоты, выделяемое реактором (формула 2.63 /14/):

Удельная тепловая нагрузка на внутренней и наружной поверхностях:

Задача 12. Электронагреватель выполнен из нихромовой проволоки диаметром d = 2 мм, длиной l = 10 м. Он обдувается холодным воздухом с температурой t = 20°С. Вычислить тепловой поток с 1 м нагревателя, а также температуры на поверхности и на оси проволоки, если сила тока I, проходящего через нагреватель, составляет 25А. Удельное электрическое сопротивление нихрома r =1,1 Ом×мм 2 /м, коэффициент теплопроводности нихрома l =17,5 Вт/м 2 ×град и коэффициент теплоотдачи от поверхности нагревателя к воздуху a=46,5Вт/м 2 ×град.

Решение: Электрическое сопротивление нагревателя:

Тепловой поток, выделяемый нагревателем на длине 1 м:

Температура поверхности проволоки будет равна:

Температура на оси проволоки нагревателя равна
(из формулы 2-147 /14/):

Задача 13. Трубка из нержавеющей стали с внутренним диаметром d₁= 7,6 мм и наружным диаметром d₂= 8 мм включена в электрическую цепь. Все тепло отводится через внутреннюю поверхность трубки. Вычислить объемную производительность источников тепла и перепад температур в стенке трубки, если по трубке пропускается ток силой I=250 А. Удельное электрическое сопротивление и коэффициент теплопроводности стали соответственно равны r=0,85 Ом×мм 2 /м, l =18,6 Вт/м×град.

Решение: Электрическое сопротивление на единицу длины трубки:

Тепловой поток на единицу длины:

Объемная производительность внутренних источников тепла:

Перепад температур в стенке трубы (формула 1.35):

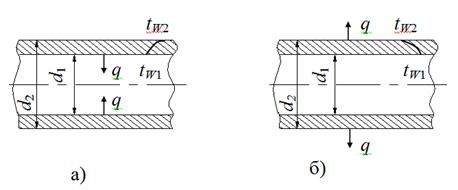
Задача 14. Через трубку из нихромовой стали диаметром 14/14,6 мм пропускается ток силой I=300А. Определить объемную теплопроизводительность источников теплоты и перепад температуры в стенке трубки в предположении, что теплота отводится:

а) только через внутреннюю поверхность трубки;

б) только через наружную поверхность трубки.

Электрическое сопротивление материала трубки r =1,17 Ом×мм 2 /м и коэффициент теплопроводности l = 7,2 Вт/м×град.

Решение: Электрическое сопротивление на единицу длины трубки:

Здесь r₁=7 мм и r₂=7,3 мм – внутренний и внешний радиусы трубки.

Тепловой поток на единицу длины:

Объемная производительность внутренних источников тепла:

а) Перепад температур в стенке трубки при отводе теплоты через внутреннюю поверхность трубки (формула 1.35):

б) Перепад температур в стенке трубки при отводе теплоты через наружную поверхность трубки (формула 1.32¢):

Задача 15. Вычислить максимальное значение температуры тепловыделяющего элемента (ТВЭЛ) ядерного реактора, имеющего форму неограниченной плоской пластины. Производительность равномерно распределенных по объему пластины внутренних источников тепла q_V =90 МВт/м 3 ,температуры поверхности пластины равны t_W1 =1500°С и t_W2 =2000°С, толщина пластины d =20 мм. Коэффициент теплопроводности материала пластины l = 17 Вт/м×град. Также определить закон изменения температуры внутри пластины и расстояние х₀ от поверхности пластины с температурой t_W1 до сечения, в котором t = t_max.

Решение: Уравнение стационарной теплопроводности для плоской пластины с внутренними источниками тепла:

Общее решение уравнения (формула 2-133/14/):

Постоянные интегрирования С₁ и С₂ будут равны:

Максимальное значение температуры будет при х=х₀.

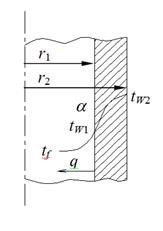
В точке х=х₀ 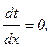т.е.:

Задача 16. Рассчитать распределение температуры в поперечном сечении тепловыделяющего элемента (ТВЭЛ), имеющего форму длинного полого цилиндра с внутренним диаметром d₁=16 мм и наружным d₂=26 мм, выполненного из урана. Коэффициент теплопроводности урана l_у= 31 Вт/м×град. Обе поверхности ТВЭЛа покрыты плотно прилегающими оболочками из нержавеющей стали толщиной

d =0,5 мм. Коэффициент теплопроводности нержавеющей стали l_ст=21 Вт/м×град. Объемная плотность тепловыделения в уране принята равномерной по сечению и равной q_V=5×10 7 Вт/м 3 . ТВЭЛ охлаждается газообразной двуокисью углерода СО₂, движущейся по внутреннему каналу с внешней стороны ТВЭЛа. Среднемассовая температура СО₂ во внутреннем канале t_f1=200°С, во внешнем канале t_f2 =240°С. Коэффициенты теплоотдачи от поверхностей оболочек к газу соответственно равны a₁=520 Вт/м 2 ×град и a₁=560Вт/м 2 ×град. Определить максимальную температуру ТВЭЛа t₀, температуры на поверхностях оболочек t_W1 и t_W2 и на поверхностях урана t₁ и t₂.

Решение: Тепло отводится через внутреннюю и наружную поверхности ТВЭЛа. При двусторонней теплоотдаче внутри цилиндрической стенки существует максимум температуры. Изотермическая поверхность, соответствующая максимальной температуре t₀, разделяет цилиндрическую стенку на два слоя. Во внутреннем слое тепло q₁ передается внутрь трубы, во внешнем слое тепло q₂ отводится наружу. Максимальной температуре соответствует диаметр d₀ или радиус r₀. Максимальные перепады температур во внешнем и внутренних слоях цилиндрической урановой стенки определяются уравнениями (формулы 1.32¢, 1.35):

Здесь r₁ и r₂, соответственно, внутренний и внешний радиусы цилиндрической стенки.

Из совместного решения этих уравнений для r₀ получим:

.

Введем в рассмотрение эффективные коэффициенты теплоотдачи от поверхностей ТВЭЛа к охлаждающему газу во внутреннем и внешнем каналах ТВЭЛа a_эф1 и a_эф2 по выражениям:

Совместное решение этих уравнений относительно r₀ приводит к выражению:

Для цилиндрической стенки тепловые сопротивления теплоотдачи на соответствующих поверхностях, определяемых диаметрами d₁, d₂, d₁-2d, d₂+2d, будут соответственно равны:

Тепловые сопротивления внутренней и внешней стенки будут равны соответственно:

, .

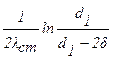
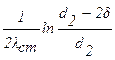
Из условий теплового баланса будем иметь:

Подставляя численные значения переменных, получим:

Плотность теплового потока на внутренней поверхности урана равна:

Температура на внутренней поверхности урана:

Плотность теплового потока на внутренней поверхности оболочки:

Температура на внутренней поверхности оболочки:

Плотности теплового потока q₂ и q_W2 и температура t₂ и t_W2 на внешней поверхности ТВЭЛа определяются аналогично:

Распределение температуры по сечению ТВЭЛа определяется уравнением (формула 1.34, r₂=r₀):

Источник