Расчет осадок фундамента. Виды деформаций. Методы расчета осадок. Методика расчета
Страницы работы
Содержание работы
РАСЧЕТ ОСАДОК ФУНДАМЕНТА
Цель расчета по второму предельному состоянию – ограничить осадку предельно допустимыми значениями, регламентированными СНиП.
1. Осадка – это деформация, происходящая в результате уплотнения грунта под действием внешних нагрузок или собственного веса грунта без коренного изменения его структуры.
2. Просадка – это деформация, возникающая в результате уплотнения грунта от действия внешних нагрузок и собственного веса грунта (а также дополнительных нагрузок – замачивание, оттаивание) с коренным изменением структуры грунта.
3. Подъем и осадка – это деформации, связанные с изменением объемов грунтов при изменении их влажности или воздействии дополнительных факторов (оттаивание, набухание, усадка, замерзание).
4. Оседание – это деформация, возникающая в результате разработки полезных ископаемых, вызывающая понижение уровня грунтовых вод (УГВ) и др.
5. Горизонтальное перемещение – это деформация, связанная с действием горизонтальных нагрузок на основание или со значительными вертикальными перемещениями при оседаниях и просадках грунтов.
Основные причины неравномерных осадок:
1. Неоднородное напряженное состояние грунтов в основании, т.е. нецентренно-нагруженный фундамент или использование различных видов фундаментов под сооружением.
2. Неравномерная сжимаемость грунтов в основании под фундаментом.
Методы расчета осадок
1. Метод послойного суммирования.
2. Метод эквивалентного слоя (метод Цытовича).
3. Метод линейно-деформированного слоя конечной толщины (метод Егорова).
1. Метод послойного суммирования
Нс – сжимаемые слои;
hА – активные слои.
Разбиваем основание на слои.
Допущения, принимаемые при расчете:
1. Грунт в основании представляет собой сплошное изотропное деформируемое тело.
2. Осадка обусловлена действием только вертикальной нагрузки, напряжения σzp.
3. Боковое расширение грунта в основании невозможно.
4. Деформация рассматривается только в пределах сжимаемой толщи Нс, ниже считается, что деформации нет.
5. Значение коэффициента β=0,8 не зависимо от характера грунта.
1. Разбиваем основание на слои толщиной hi ≤ 0,4b.
2. Определяем вертикальные напряжения от веса грунта в каждом слое:
где γ´ — удельный вес грунта выше подошвы фундамента;
d – глубина залегания фундамента;
γi– удельный вес i-го слоя грунта;
3. Определяем вертикальные напряжения от действительной нагрузки на грунт и строим эпюру:
где α – безразмерный коэффициент, определяют по приложению СНиП.
4. Нижней границы достигают, когда σzp = 0,2σzqв грунтах с модулем деформации Е ≥ 5 МПа; σzp = 0,1σzq для грунтов с Е 2 для однородных или слоистых оснований, в которых сжимаемость отдельных слоев грунта мало отличается друг от друга.
Сущность метода заключается в следующем:
Грунтовое основание на всю глубину сжатия принимается однородным, с равномерно нагруженными слоями, т.е. возможно замещение эквивалентным слоем грунта.
Эквивалентный слой — это слой грунта, осадка которого (S2) при сплошной нагрузке равна осадке фундамента (S1) при той же нагрузке и тех же условиях.
Допущения, принимаемые при расчете:
1. Грунт однороден в пределах сжимаемой толщи;
2. Грунт есть линейно-деформируемое тело (т.е. деформация пропорциональна напряжению).
Для однородного основания
Осадка определяется по формуле:
mυ – коэффициент относительной сжимаемости грунта: 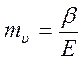
Р0 – дополнительное вертикальное давление сверх расчетного (из прил. СНиП).
где ω – коэффициент осадки, зависящий от формы площади нагружения, от жесткости фундамента и месторасположения точки, в которой определяется осадка.
А – коэффициент, определяемый как 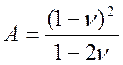
А·ω – коэффициент эквивалентного слоя, определяемый по табл. Цытовича.
Для слоистого основания
Осадка определяется по формуле:
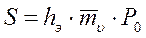
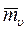
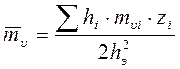
mυi – коэффициент относительной сжимаемости i-го слоя грунта;
zi – расстояние от нижней границы сжимаемой толщи до середины i-го слоя.
Сжимаемая толща или активная зона – это такая толща грунта, ниже которой деформация не учитывается (Нс
3. Метод линейно-деформированного слоя
Метод используется в следующих случаях:
1) Если в пределах сжимаемой толщи залегает слой грунта с модулем деформации Е ≥ 100 МПа и толщиной h1 с соблюдением условия:
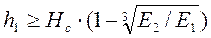
Е2 – модуль деформации подстилающего слоя грунта (ниже прослойки h1).
В этом случае толщина линейно-деформированного слоя Н ограничивается кровлей грунта с модулем Е1.
2) Если ширина или диаметр фундамента больше 10 м и модуль деформации Е > 10 МПа.
где Н – толщина или мощность линейно-деформированного слоя;
— для оснований, сложенных пылевато-глинистыми грунтами
— для оснований, сложенных песчаными грунтами
Для нахождения промежуточных значений применяется интерполяция.
 |
Осадка определяется по формуле:
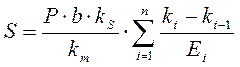
Р – среднее давление под подошвой фундамента;
kS и km– определяются по табл. 2 и 3 прил. 2 СНиП;
ki и ki—1 – коэффициенты, определяемые по табл. 4 прил. 2 СНиП, зависящие от формы фундамента и соотношения сторон;
Еi – модуль деформации i-го слоя грунта;
n – число слоев, различающихся по сжимаемости в пределах рассчитываемой величины сжимаемого слоя.
Допущения, принимаемые при расчете:
1. Мощность несущего слоя грунта ограничена.
2. Деформация прямо пропорциональна напряжениям.
3. Учтено влияние всех составляющих напряжений.
4. Жесткость фундамента не учитывается.
Достоинства метода: самый точный метод.
Источник
Методы расчёта осадок оснований.
При проектировании оснований сооружений одним из основных условий является ограничение перемещений предельными их значениями, т.е. производится расчет по второй группе предельных состояний.
Совместная деформация основания и сооружения может характеризоваться:
· абсолютной (конечной) осадкой отдельного фундамента S;
· средней осадкой основания сооружения;
· относительной неравномерностью осадок фундаментов ∆S/L;
· креном фундамента или сооружения в целом i;
· горизонтальным перемещением фундамента или сооружения в целом и.
Расчет оснований гидротехнических сооружений по второй группе предельных состояний (по деформациям) заключается в выполнении условий:

где Su; Su ; UU; iU — соответственно предельные абсолютные и средние осадки, горизонтальные перемещения и крены, при которых гарантируются нормальные условия эксплуатации и обеспечивается требуемая долговечность сооружения (принимаются по СНиП 2.02.01—83*).
Левая часть неравенства S ≤ Su характеризует деформируемость грунтов основания. Она учитывает общие инженерно-геологические условия строительной площадки, особенности напластования и свойств грунтов основания.
Правая часть неравенства S≤Su учитывает особенности проектируемых зданий и сооружений, условия их эксплуатации и напряженные состояния надземных частей зданий и сооружений. Чем ближе S и Su, тем экономичнее будут запроектированы основание и фундамент.
Для определения осадок основания выбирается расчетная схема с учетом показателей механических свойств, характера их напластования в основании и особенностей сооружения.
Наиболее употребимыми при проектировании являются следующие методы расчета осадки:
· определение осадки слоя грунта при сплошной неравномерной нагрузке (основная задача);
· определение осадки неоднородного (слоистого) грунта основания (линейно-деформируемого полупространства) — метод послойного суммирования;
· определение осадок линейно-деформируемого слоя конечной толщины;
· расчет осадки во времени;
· определение неравномерности осадок и крена фундамента.
44.Расчёт осадки слоя грунта при сплошной нагрузке (основная задача).
Основная задача. При действии сплошной нагрузки, распространенной на значительные расстояния в стороны, слой грунта испытывает только сжатие без возможности бокового расширения, т.е. аналогично компрессионному сжатию (рис. 7.10,а).
Рис. 7.10. Схема испытания грунта при сплошной нагрузке: а — схема нагрузки; б — компрессионная кривая
В этом случае будем иметь строго одномерную задачу компрессионного уплотнения грунтов и для определения полной стабилизированной осадки слоя грунта воспользуемся результатами компрессионных испытаний (см. рис. 7.10,б).
Осадка грунта происходит из-за изменения объема за счет уменьшения пористости при увеличении внешнего давления, а объем твердых частиц, как было ранее сказано, при этом остается неизменным.
Выделим в рассматриваемом слое (см. рис. 7.10,а) на всю его высоту цилиндр площадью поперечного сечения А, принимая во внимание, что объем
твердых частиц Vs в единице объема грунта равен m = 1 / 1 + e, так как m+n=1.
Приравняем Vs выделенного цилиндра до приложения нагрузки к объему после полного компрессионного уплотнения под нагрузкой.

где е1 — начальный коэффициент пористости, соответствующий условиям естественного залегания; е2 — то же, после действия внешней нагрузки; h — высота слоя грунта;
h’ — конечная (стабилизированная после уплотнения) высота слоя грунта. Сократив обе части уравнения (7.4), получим
формула (7.5)
Согласно рис. 7.10,а осадка S равна разности высот грунта до уплотнения нагрузкой и после, тогда получим
Таким образом, осадка слоя грунта при сплошной нагрузке определяется по формуле

Учитывая, что изменение коэффициента пористости прямо пропорционально изменению давления, т.е. е1 — е2 = m0(Р2— Р1) = m0P, получим

Подставив (7.7) в (7.6) получим

где m0 / 1+e1 = mv есть коэффициент относительной сжимаемости грунта.
Подставляя в (7.8), получим наиболее простой вид формулы для осадки слоя грунта при сплошной нагрузке

где β — коэффициент, который зависит от коэффициента относительной поперечной деформации грунта (аналогично коэффициенту Пуассона): для песков β = 0,8; супесей β = 0,7; суглинков β = 0,5; глин β = 0,4.
Эта формула (7.10) справедлива для любых грунтов в пределах линейной зависимости между напряжениями и общими деформациями.
Источник
Методы расчета осадок фундаментов
Как было уже отмечено, что из четырех составляющих частей осадки в данном разделе рассматривается только осадка уплотнения, т. е. осадка, происходящая вследствие деформации грунта под воздействием напряженного состояния, возникающего от нагрузки, передаваемой фундаментом на грунт основания. Развивается эта осадка во времени, как правило, медленно (в течение нескольких лет после возведения здания). Медленное нарастание деформаций грунтов связано с развитием деформаций ползучести пленочной воды, а также с постепенным выдавливанием воды из пор грунта основания при водонасыщенном его состоянии.
Поскольку конструкции здания или сооружения получают наибольшие деформации при полном развитии осадки в конце срока стабилизации ограничивает эти значения осадок, называемые конечными или просто осадками. Последний термин, как более краткий, будет использован в дальнейшем, так как ниже рассматривается расчет только конечных осадок. Таким образом, осадкой фундамента называется полное вертикальное перемещение его вследствие деформации толщи грунта основания, медленно развивающейся во времени. Осадкой слоя грунта называется величина, на которую уменьшается его толщина вследствие деформации грунта этого слоя. Разработано семнадцать методов расчета осадок. Однако в проектной практике в большинстве случаев пользуются двумя основными методами: методом суммирования и методом эквивалентного слоя. Анализ всех методов расчета занял бы много времени, поэтому остановимся лишь на некоторых из них.
Определение осадки методом суммирования
Рассматриваемый метод расчета основан на следующих допущениях: 1) грунт под фундаментом не имеет бокового расширения; 2) вертикальные деформации слоев грунта прямо пропорциональны напряжениям pz, убывающим с глубиной; 3) на глубинах, где дополнительное напряжение pz составляет менее 20% от веса вышележащих слоев грунта (природное давление), считается, что грунт не испытывает деформаций; 4) напряжения рz определяются под центром загружения методами теории упругости без учета изменения деформативных характеристик грунта по глубине; 5) безразмерный коэффициент р, зависящий от коэффициента пикового расширения грунта, принимается равным 0,8 для всех видов грунтов и рассматривается как коэффициент, корректирующий упрощенную расчетную схему; 6) жесткость фундаментов и надфундаментных конструкций не учитывается. На основе перечисленных допущений расчет осадки фундамента производится по формуле:
где n — число слоев, на которые разбита сжимаемая толща основания; hi — толщина i-го слоя грунтов в см; Ei — модуль общей деформации i-го слоя в кГ/см 2 ; β — безразмерный коэффициент, равный 0,8; pZi — полусумма вертикальных нормальных напряжений в кГ/см 2 , возникающих на верхней и нижней границах i-го слоя грунта от давления, передаваемого фундаментом, вычисляемых по формуле (39). В случае учета влияния загружения соседних фундаментов дополнительно от каждого учитываемого фундамента вертикальные нормальные напряжения рассчитываются по формуле (42). При определении мощности сжимаемой толщи основания руководствуются условием:
где pz — вертикальные напряжения на глубине z, возникающие от загружения рассматриваемого фундамента и определяемые по формуле (39). В тех случаях, когда необходимо учесть загружения соседних фундаментов, pz вычисляется по (42); Рбг — природное давление, определяемое по формуле (37). СНиП рекомендует следующий прием оценки необходимости учета загружения соседних фундаментов.
Считается, что осадки отдельных фундаментов следует определять с учетом влияния, нагрузок от соседних фундаментов в тех случаях, когда имеет место условие: Кг Lф ≤ Lг, (49) где Lф — фактическое расстояние между осями фундаментов в см; Lг— расстояние, получаемое по графикам (см. рис. 13), в см; Кт — коэффициент, определяемый по формуле:
b — ширина подошвы фундамента, необходимость учета влияния которого рассматривается, в см. Е — модуль деформации грунта, принимаемый средним в пределах сжимаемой толщи, в кГ/см 2 ; 0,6 — коэффициент, имеющий размерность, в см 3 /кГ. Величина Lг для прямоугольных фундаментов с промежуточным значением отношения l/b определяется интерполяцией.
Рис. 13. Графики для определения расстояния между осями фундаментов в случае учета влияния загружения соседнего фундамента а — для квадратного фундамента; б —для прямоугольного фундамента при l/b ≥ 5.
Поскольку метод, рекомендованный СНиПом, может быть использован далеко не во всех случаях (например, при наличии двух соседних фундаментов, расположенных на различном расстоянии от рассчитываемого), целесообразно принять простейшую приближенную оценку необходимости учета загружения соседних фундаментов или поверхности грунта полезной нагрузкой.
В порядке первого приближения следует учитывать все нагрузки, приложенные на расстоянии менее мощности сжимаемой толщи рассчитываемого фундамента. Мощность этой толщи сначала приходится оценивать ориентировочно. В ходе расчета она уточняется в зависимости, от напряжений как от загрузки рассчитываемого фундамента, так и соседних.
Расчет осадки фундамента методом эквивалентного слоя
Метод суммирования, как показывают приведенные выше примеры, громоздок. Кроме того, он не является точным, так как основан на ряде ранее отмеченных допущений. Во многих случаях расчет осадки фундаментов может быть произведен по более простому методу эквивалентного слоя. Основные допущения рассматриваемого метода при мощном слое однородного грунта: 1) однородный грунт имеет бесконечное распространение и пределах полупространства; 2) деформации в пределах полупространства пропорциональны напряжениям, т. е. полупространства линейно деформируемо; 3) деформации полупространства устанавливаются методами теории упругости. Из теории упругости известно, что осадка поверхности линейно деформируемого полупространства может быть найдена по формуле:
где ω — коэффициент осадки, зависящий от формы площади загружения, жесткости фундамента и места расположения точки, в которой определяется осадка; рд — интенсивность приложенного давления, деформирующего рассматриваемое полупространство (грунты основания), в кГ/см 2 ; b — ширина площади загружения в см; Е — модуль общей деформации грунта в кГ/см 2 ; μ — коэффициент бокового расширения грунта основания. Эта формула учитывает ограниченное боковое расширение грунтов основания и деформации их под действием всех компонентов напряжений.
Расчет осадок при слоистом напластовании грунтов
Для определения осадки фундамента при слоистом залегании различных грунтов предложено приближенное решение. Рекомендовано эпюры напряжений сложных очертаний заменить на суммарную эквивалентную треугольную эпюру уплотняющих давлений (рис. 16), под действием которой разовьется осадка, равная осадке, определяемой по формуле (56). Из этого положения находят высоту треугольной эпюры уплотняющих давлений:
Величина Н рассматривается как мощность активной зоны, в пределах которой практически деформируется грунт под действием уплотняющих давлений, распределенных по треугольной эпюре. В таком случае при наличии нескольких слоев грунта в пределах мощности активной зоны рекомендует определять среднее значение коэффициента относительной сжимаемости а0m по формуле:
Где hi -толщина i-го слоя грунта в пределах активной зоны, равной 2 hs в см; а0i— коэффициент относительной сжимаемости i-го слоя
грунта в см 2 /кГ; Zi — расстояние от точки, соответствующей глубине 2 hs, до середины i-го слоя (рис. 17) в см; hs — мощность эквивалентного слоя в см; п — число слоев в активной зоне. Формулой (61) можно пользоваться и при непрерывном изменении приведенного коэффициента сжимаемости грунта по глубине отдельного слоя. В этом случае слой надо разбить на части, в пределах которых можно принять значение коэффициента относительной сжимаемости постоянным.
Зная средний коэффициент относительной сжимаемости слоистой толщи грунтов, легко определить осадку фундамента по уже известной формуле: S = hsa0mPд(62) В этом случае при определении величины коэффициента эквивалентного слоя по табл. 13 принимают среднее значение коэффициента бокового расширения грунта μ.
Рис.16. Расчетная схема эквивалентной эпюры.
Расчет осадки фундамента по методу Егорова
При расчете осадки фундамента исходят из следующих допущений: 1) деформирующаяся толща грунтов ограничена по мощности; 2) деформации в пределах каждого слоя пропорциональны напряжениям, т. е. грунт каждого слоя является линейно деформируемым; 3 деформации отдельных слоев устанавливаются с учетом всех составляющих напряжений; 4) осадка фундамента равна средней величине осадки поверхности грунта под действием равномерно распределенной нагрузки; 5) жесткость фундамента не учитывается; 6) распределение напряжений в слое грунта принимается в соответствии с задачей однородного полупространства, а жесткость подстилающего слоя учитывается поправочным коэффициентом М.
Выведена формула для конечной осадки:
Где b — ширина фундамента; рд — среднее давление, под действием которого уплотняется грунт основания; Еi — модуль деформации i-гo слоя грунта; Кi — коэффициент, зависящий от формы подошвы и отношения Н/b , определяемый по табл. 14. М — коэффициент, учитывающий концентрацию напряжений при наличии жесткого подстилающего слоя (принимается по табл. 14). Коэффициент М одновременно учитывает отсутствие перемещений по контакту сжимаемого слоя грунта и подстилающего недеформируемого массива. Величина М зависит от коэффициента Пуассона μ = 0,30. Мощность активной зоны Н, в пределах которой следует учитывать деформации грунтов основания, по этому методу установить нельзя, поэтому при отсутствии подстилающих скальных пород определяет ее в соответствии с методом суммирования. Кроме того, этот метод пока не позволяет определять осадку фундамента с учетом влияния загружения соседних площадей и фундаментов. Однако весьма ценно, что по этому методу определяются деформации не под действием одного компонента напряжений, а с учетом напряженного состояния в пределах каждого рассматриваемого линейно деформируемого слоя.
Расчет крена фундамента
При внецентренной нагрузке напряжения по подошве фундамента распределяются по треугольной или трапециевидной эпюре. В этом случае фундамент, кроме вертикального перемещения (осадки), будет поворачиваться. Этот поворот обычно выражается величиной крена. Когда грунт может рассматриваться как линейно деформируемая среда, осадку и крен легко определить раздельно. Осадку фундамента определяют обычным способом как для центрально нагруженного фундамента. Крен, т. е. тангенс угла поворота фундамента, можно вычислить по формулам. Крен продольной оси прямоугольного фундамента определяется по формуле:
и крен поперечной оси фундамента — по формуле:
где ЕСР и μср — модуль деформации (в кГ/см 2 ) и коэффициент бокового расширения грунта, принимаемые средними в пределах сжимаемой толщи; k1 и k2 — безразмерные коэффициенты, определяемые в зависимости от соотношения сторон подошвы фундамента Кn= l/b по графикам, приведенным на рис. 19.
Рис.19. Графики для определения коэффициентов, необходимых для вычисления кренов фундаментов а—коэффициента k1;б—коэффициента k2;
N H — вертикальное усилие от нормативных нагрузок, действующее в плоскости подошвы фундамента с эксцентриситетом, в кГ; l и b — соответственно большая и меньшая стороны подошвы фундамента в см; е1 — эксцентриситет усилия N H в плоскости подошвы фундамента (по продольной его оси в см; е2 — то же, по поперечной оси фундамента в см. Для квадратных фундаментов принимают к1 = к2=0,5. Рекомендуются следующие значения коэффициента μ для различных грунтов: крупнообломочных = 0,27 песков и супесей = 0,30 суглинков = 0,35 глин = 0,42
Крен отдельного круглого фундамента б при эксцентричном его загружении определяется по формуле:
где е — эксцентриситет усилия N a в плоскости подошвы фундамента в см; r — радиус фундамента в см. При форме подошвы фундамента в виде правильного многоугольника крен вычисляют по формуле (66). В этом случае за радиус принимают величину:
где F — площадь подошвы фундамента в см 2 . Крен кольцевых фундаментов определяется, по формуле (20):
где ω (п)—коэффициент, зависящий от величины п = rвн / rнар rвн — внутренний радиус подошвы кольцевого фундамента (радиус вырезки); rнар — наружный радиус подошвы фундамента.
Фундаменты получают крен не только при внецентренном приложении нагрузки. Крен фундамента или сооружения может развиваться вследствие неодинаковой сжимаемости грунтов под отдельными их частями, а также различия во влиянии загружения соседних фундаментов или площадей. В этих случаях правильнее всего вычислить осадки в ряде точек, расположенных по оси фундамента, крен которой определяется. Полученную кривую следует аппроксимировать прямой, наклон этой прямой и будет креном фундамента. Следовательно, такие вычисления трудоемки и проводятся в исключительных случаях. Для упрощения СНиП рекомендуют определять крен фундаментов в случае взаимного влияния по формуле:
где S1 и S2 — осадки, подсчитанные у краев фундамента, в см; b — размер фундамента в направлении крена в см.
Осадки краев фундамента определяются методом угловых точек, который позволяет учитывать и влияние загружения соседних фундаментов. При определении осадок S1 и S2 руководствуются напластованием грунтов под рассматриваемыми краями фундамента. Так как непосредственно под краем фундамента напряжения и грунте равны только половине интенсивности давления по подошве фундамента, под действием котором деформируются грунты основания, получаемые результаты будут весьма приближенными.
Более точные результаты можно получить, если осадки S1 и S2 определять для точек А и В (рис. 20), расположенных под фундаментом и удаленных от края его на расстояние 10—15% размера подошвы фундамента вдоль оси, крен котором вычисляется. Крен жестких сооружений на отдельных фундаментах также может быть найден по формуле (69). При этом S1 и S2 будут осадки отдельных фундаментов, лежащих в направлении определяемого крена, а размер b принимается равным расстоянию между осями этих фундаментов (см. рис. 5).
При проектировании высоких сооружений (дымовые трубы, водонапорные башни, телевизионные мачты и т. п.) определяют крен сооружения от действия ветровой нагрузки. Кроме крена, при значительных постоянных горизонтальных усилиях возникает необходимость рассчитывать фундаменты на горизонтальное смещение. Такого рода расчеты производят в соответствии с расчетами гидротехнических сооружений.
Рис.20. Расчетная схема для определения крена фундамента; а — разрез; б — план
Источник



















