- Определение напряжений по подошве фундаментов и сооружений
- 5.5.4. Расчет деформаций основания (ч. 1)
- А. ОСАДКИ ФУНДАМЕНТОВ
- ТАБЛИЦА 5.17. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА kc
- ТАБЛИЦА 5.18. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА km
- ТАБЛИЦА 5.19. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА k
- ТАБЛИЦА 5.20. ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ k0, k1, k2, k3
- ТАБЛИЦА 5.21. ЗНАЧЕНИЕ КОЭФФИЦИЕНТА kr
- ТАБЛИЦА 5.22. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА ω
Определение напряжений по подошве фундаментов и сооружений
Общие положения.При взаимодействии фундаментов и сооружений с грунтами основания на поверхности контакта возникают контактные напряжения. Знание контактных напряжений необходимо как для расчета напряжений в основании, создаваемых сооружением, так и для расчетов самих конструкций.
Отметим, что расчет сооружений на действие контактных напряжений обычно рассматривается в курсе строительной механики.
Характер распределения контактных напряжений зависит от жесткости, формы и размеров фундамента или сооружения и от жесткости (податливости) грунтов основания. Различают три случая, отражающих способности сооружения и основания к совместной деформации:
1) абсолютно жесткие сооружения, когда деформируемость сооружения ничтожно мала по сравнению с деформируемостью основания, и при определении контактных напряжений сооружение можно рассматривать как недеформируемое;
2) абсолютно гибкие сооружения, когда деформируемость сооружения настолько велика, что оно свободно следует за деформациями основания;
3) сооружения конечной жесткости, когда деформируемость сооружения соизмерима с деформируемостью основания; в этом случае они деформируются совместно, что вызывает перераспределение контактных напряжений.
Характерными примерами абсолютно жестких конструкций являются массивные фундаменты под мостовые опоры, дымовые трубы, тяжелые прессы, кузнечные молоты и т. д., абсолютно гибких – земляные насыпи, днища металлических резервуаров и т. п. Большинство сооружений (плитные фундаменты, балки, ленточные фундаменты) по условиям работы конструкций имеют конечную жесткость.
Критерием оценки жесткости сооружения может служить показатель гибкости по М.И. Горбунову-Посадову
е ≈ 10 (El 3 /Eкh 3 ), (8.1)
где Еи Ек — модули деформации грунта основания и материала конструкции; l и h— длина и толщина конструкции.
Конструкция сооружения или фундамента считается абсолютно жесткой, если t≤1. В первом приближении жесткость конструкции можно оценить исходя из соотношения ее толщины и длины. При h/l>1/3 конструкция может рассматриваться как абсолютно жесткая.
Существенное значение имеет также соотношение длины l и ширины b сооружения. При 1/b≥0 распределение контактных напряжений соответствует случаю плоской задачи, при. l/b 2 ) – цилиндрическая жесткость полосы; f(x) –интенсивность заданной на полосу нагрузки; р(х) – интенсивность неизвестной эпюры контактных напряжений. Напомним, что индекс «к» относится к конструкции; следовательно, Еки vк – соответственно модуль упругости и коэффициент Пуассона материала полосы; Iк – момент инерции ее поперечного сечения.
В уравнении (8.2) содержатся две неизвестные величины: w(x) и р(х). Следовательно, для решения задачи необходимо введение дополнительного условия. Это условие определяется в зависимости от принятия той или иной модели: местных упругих деформаций или упругого полупространства.
Модель местных упругих деформаций.Предпосылки этой модели впервые были сформулированы русским академиком Фуссом в 1801 г., а сама модель разработана в 1867 г. Винклером для расчетов железнодорожных шпал. В дальнейшем модель местных упругих деформаций была развита в работах Н. П. Пузыревского, С. П. Тимошенко, А. Н. Крылова, П. Л. Пастернака и др.
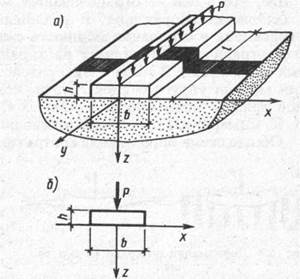
Рис. 8.2. Схема балки (а) и расчетная схема для случая плоской задачи (б)
Согласно этой модели, реактивное напряжение в каждой точке поверхности контакта прямо пропорционально осадке поверхности основания в той же точке:
p(x) = kw(x), (8.3)
где к — коэффициент пропорциональности, часто называемый коэффициентом постели, Па/м.
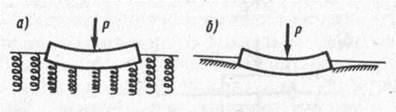
Схема деформирования такого основания показана на рис. 8.3, а. Видно, что в соответствии с моделью местных упругих деформаций осадки поверхности основания за пределами габаритов фундамента отсутствуют, т. е. фундамент как бы установлен на пружинах, сжимающихся только в пределах его контура.
Рис. 8.3. Деформации поверхности основания: а – по модели упругих деформаций; б – по модели упругого полупространства
Модель упругого полупространства.Эта модель была предложена Г. Э. Проктором в 20-х годах нашего столетия и развита благодаря работам Н. М. Герсеванова, М. И. Горбунова-Посадова, Б. Н. Жемочкина, А. П. Синицына и других ученых.
В отличие от предыдущей модели в этом случае поверхность грунта оседает как в пределах площади загрузки, так и за ее пределами (рис. 8.3, б), причем кривизна прогиба зависит от механических свойств грунтов и мощности сжимаемой толщи в основании.
В случае плоской деформации прогиб поверхности под действием сосредоточенной силы Р описывается уравнением
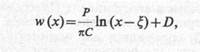
где С = Е/(1 – ν 2 ) – коэффициент жесткости основания; х — координата точки поверхности, в которой определяется осадка; ζ — координата точки приложения силы Р; D — постоянная интегрирования. При определении прогибов поверхности от действия распределенной нагрузки уравнение (8.4) следует проинтегрировать по площади загружения.
Недостаток модели упругого полупространства заключается в том, что в ней не ограничивается мощность сжимаемой толщи в основании сооружения. В реальных условиях взаимодействия фундамента и основания мощность сжимаемой толщи обычно бывает ограничена, что влияет на характер распределения контактных напряжений. В связи с этим разработаны различные модификации модели упругого слоя грунта, подстилаемого недеформируемой толщей, приведенные в работах О. Я. Шехтер, К. Е. Егорова, И. К. Самарина, Г. В. Крашенинниковой и др.
Общая схема определения контактных напряжений с использованием указанных выше моделей заключается в совместном решении уравнения (8.2) и условия (8.3) в случае модели местных упругих деформаций или уравнений (8.2) и условия типа (8.4) в случае модели упругого полупространства. Методы решения этих задач приведены, например, в учебнике П. Л. Иванова (1991).
Для практических расчетов контактных напряжений используются приведенные в табличной форме решения М. И. Горбунова-Посадова, Б. Н. Жемочкина, А. П. Синицьша, Г. В. Крашенинниковой и др. Наиболее полные сведения по этому вопросу представлены в монографии М. И. Горбунова-Посадова, Т. А. Маликовой, В. И. Соломина «Расчет конструкций на упругом основании», удостоенной в 1987 г. Государственной премии СССР.
Область применения различных моделей. Практика расчетов показывает, что модель местных упругих деформаций позволяет получить хорошее совпадение с действительностью при возведении фундаментов на сильносжимаемых грунтах (при Е≤ 5 МПа), на лёссовых просадочных грунтах, а также при ограниченной толще сжимаемых грунтов, подстилаемых практически недеформируемыми, например скальными породами. Модель упругого полупространства применима при наличии в основании достаточно плотных грунтов и при не слишком больших площадях опорных поверхностей. Для сооружений с площадью опирания в десятки и сотни квадратных метров более близкие к действительности результаты дает модель упругого слоя ограниченной мощности.
Контактные напряжения на подошве центрально-загруженных абсолютно жестких фундаментов.При определении контактных напряжений в этом случае исходят из того, что вертикальные перемещения любой точки поверхности грунта в уровне подошвы одинаковы, т. е. w(x,у)=const. Тогда для круглого в плане фундамента контактные напряжения определятся выражением
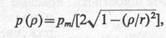
где рm — среднее напряжение под подошвой фундамента радиусом r; ρ — расстояние от центра фундамента до точки, в которой определяется ордината контактного напряжения р(ρ).
Аналогичным образом определяются и контактные напряжения под жестким полосовым фундаментом в случае плоской задачи:
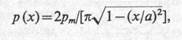
где х — расстояние от середины фундамента до рассматриваемой точки; а = b/2— полуширина фундамента.
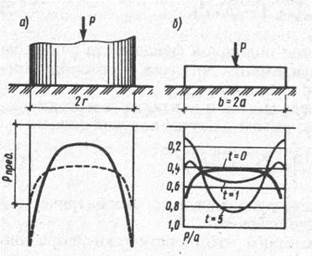
Приведенные решения показывают, что теоретически эпюра контактных напряжений под жестким фундаментом имеет седлообразный вид с бесконечно большими значениями напряжений по краям (при ρ = r или x=b/2). Однако вследствие пластических деформаций грунта в действительности контактные напряжения характеризуются более пологой кривой и у края фундамента достигают значений, соответствующих предельной несущей способности грунта (пунктирная кривая на рис. 8.4, а).
Рис. 8.4. Эпюры контактных напряжений: a — под жестким круглым штампом; б— под плоским фундаментом при различном показателе гибкости
Изменение показателя гибкости существенно сказывается на изменении характера эпюры контактных напряжений. На рис. 8.4, б в качестве примера приведены контактные эпюры для случая плоской задачи при изменении показателя гибкости t от 0 (абсолютно жесткий фундамент) до 5.
Как отмечалось выше, достоверное знание контактных напряжений необходимо для расчетов конструкции фундаментов сооружений, взаимодействующих с грунтом. При расчетах напряжений в основаниях от действия нагрузок, соответствующих контактным напряжениям, часто оказывается возможным вводить существенные упрощения. Это связано с тем, что неравномерное распределение контактных напряжений по подошве фундамента оказывает заметное влияние на изменение напряжений лить в верхней части основания на глубину порядка половины ширины фундамента.
Упрощенное определение контактных напряжений. Если контактные напряжения по подошве фундамента определяются для последующих расчетов напряжений в основании, то допускается независимо от жесткости фундамента .использовать формулы внецентренного сжатия. Тогда для центрально-нагруженного силой Р фундамента будет иметь место равномерное распределение напряжений по его подошве: р=Р/А, где А — площадь фундамента. В случае плоской задачи при нагружении фундамента силой Р и моментом М, действующим в этой плоскости, краевые значения контактных напряжений определятся выражением
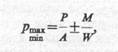
где W — момент сопротивления площади подошвы выделенной полосы фундамента. Распределение контактных напряжений между этими значениями будет иметь линейный характер.
Теперь уже распределение напряжений в основании ниже подошвы фундамента можно рассчитать, если рассматривать полученную таким образом эпюру контактных напряжений как абсолютно гибкую местную нагрузку, действующую в этой плоскости.
Источник
5.5.4. Расчет деформаций основания (ч. 1)
А. ОСАДКИ ФУНДАМЕНТОВ
Определение осадки методом послойного суммирования. В методе послойного суммирования приняты следующие допущения:
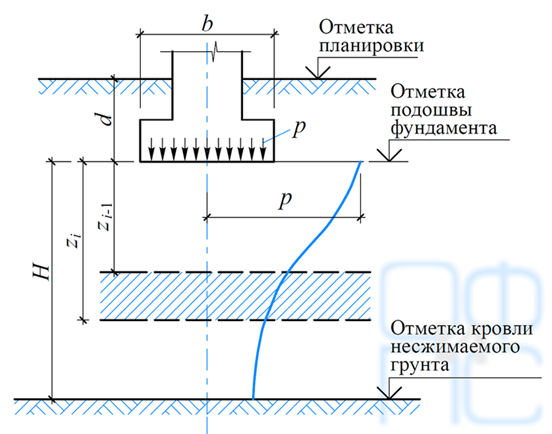
- – осадка основания вызывается дополнительным давлением р0 , равным полному давлению под подошвой фундамента р за вычетом вертикального нормального напряжения от собственного веса грунта на уровне подошвы фундамента: р0 = р – σzg,0 (при планировке срезкой принимается σzg,0 = γ´d , при отсутствии планировки и планировке подсыпкой σzg,0 = γ´dn , где γ´ — удельный вес грунта, расположенного выше подошвы; d и dn — глубина заложения фундамента от уровня планировки и природного рельефа);
- – распределение по глубине дополнительных вертикальных нормальных напряжений σzp от внешнего давления р0 принимается по теории линейно-деформируемой среды как в однородном основании (см. п. 5.2);
- – при подсчете осадок основание делится на «элементарные» слои, сжатие которых определяется от дополнительного вертикального нормального напряжения σzp , действующего по оси фундамента в середине рассматриваемого слоя;
- – сжимаемая толща основания ограничивается глубиной z = Нс , где выполняется условие
Если найденная по условию (5.59) нижняя граница сжимаемой толщи находится в слое грунта с модулем деформации Е z = Hc , нижняя граница сжимаемой толщи определяется исходя из условия σzp = 0,1σzg .
Осадка основания s методом послойного суммирования определяется по формуле
где β — безразмерный коэффициент, равный 0,8; σzp,i — среднее значение дополнительного вертикального нормального напряжения в i -м слое грунта, равное полусумме указанных напряжений на верхней zi-1 и нижней zi границах слоя по вертикали, проходящей через центр подошвы фундамента; hi и Еi — соответственно толщина и модуль деформации i -го слоя грунта; n — число слоев, на которое разбита сжимаемая толща основания.
При этом распределение вертикальных нормальных напряжений по глубине основания принимается в соответствии со схемой, приведенной на рис. 5.26.
Дополнительные вертикальные нормальные напряжения по вертикали, проходящей через центр рассматриваемого фундамента, на глубине z от его подошвы определяются:
σzp — от дополнительного давления р0 под подошвой рассчитываемого фундамента [см. формулу (5.12)]; σzp,A — от дополнительного давления р0j под подошвой j -го влияющего фундамента методом угловых точек по формуле (5.18).
Суммарное дополнительное напряжение по оси рассчитываемого фундамента с учетом влияния нагрузок от соседних фундаментов определяется по формуле (5.19).
Пример 5.12. Рассчитать осадку фундамента Ф-1 здания с гибкой конструктивной схемой с учетом влияния нагрузки на фундамент Ф-2 по условиям примера 5.2 (см. рис. 5.11) при следующих данных. С поверхности до глубины h + h1 = 6 м залегает песок пылеватый со следующими характеристиками, принятыми по справочным таблицам (см. гл. 1): γs = 26,6 кН/м 3 ; γ = 17,8 кН/м 3 ; ω = 0,14; е = 0,67; сII = 4 кПа; φII = 30°; E = 18 000 кПа. Ниже залегает песок мелкий с характеристиками: γs = 26,6 кН/м 3 ; γ = 19,9 кН/м 3 ; ω = 0,21; е = 0,62; сII = 2 кПа; φII = 32°; E = 28 000 кПа. Уровень подземных вод находится на глубине 6,8 м от поверхности. Суммарная нагрузка на основание от каждого фундамента (с учетом его веса) N = 5,4 МН.
Решение. По формуле (5.21) удельный вес песка мелкого с учетом взвешивающего действия воды
γsb = (26,6 – 10)/(1 + 0,62) = 10,2 кН/м 3 .
По табл. 5.11 находим: γc1 = 1,2 и γc2 = 1. По табл. 5.12 при φII = 30° находим: Mγ = 1,15; Мq = 5,59; Мc = 7,95. Поскольку характеристики грунта приняты по таблицам, k = 1,1.
По формуле (5.29) получаем:

Среднее давление под подошвой
р = 5400/4 2 = 338 кПа R = 341 кПа;
дополнительное давление на основание
Дополнительные вертикальные нормальные напряжения в основании фундаментов Ф-1 и Ф-2 подсчитаны в примере 5.2, приведены в табл. 5.6 и показаны на рис. 5.11. Дополняем табл. 5.6 подсчетом напряжений от собственного веса грунтов σzg для определения нижней границы сжимаемой толщи (табл. 5.16).
Из табл. 5.16 видно, что нижняя граница сжимаемой толщи под фундаментом Ф-1 находится на глубине z1 = 8,0 м (при учете нагрузки только на этот фундамент) и на глубине z2 = 8,8 м (при учете влияния фундамента Ф-2).
ТАБЛИЦА 5.16. К ПРИМЕРУ 5.12
| z , м | σzp1 | σzp2 | σzp | σzg | 0,2 σzg | E |
| 0 | 300 | 0 | 300 | 36 | 7 | 18 000 |
| 0,8 | 288 | 0 | 288 | 50 | 10 | |
| 1,6 | 240 | 0 | 240 | 64 | 13 | |
| 2,4 | 182 | 1 | 183 | 78 | 16 | |
| 3,2 | 135 | 2 | 137 | 93 | 19 | |
| 4,0 | 101 | 3 | 104 | 107 | 21 | |
| 4,8 | 77 | 4 | 81 | 123 | 25 | 28 000 |
| 5,6 | 60 | 5 | 65 | 131 | 26 | |
| 6,4 | 48 | 6 | 54 | 139 | 28 | |
| 7,2 | 39 | 6 | 45 | 147 | 29 | |
| 8,0 | 32 | 7 | 39 | 156 | 31 | |
| 8,8 | 27 | 7 | 34 | 164 | 33 |
Примечание. Значения напряжений и модуля даны в кПа.
Определяем осадку фундамента Ф-1 по формуле (5.60):
без учета влияния Ф-2

с учетом влияния Ф-2

Определение осадки основания с использованием схемы линейно-деформируемого слоя.
Средняя осадка фундамента на слое конечной толщины (рис. 5.27) определяется по формуле [4]
где р — среднее давление под подошвой фундамента; b — ширина прямоугольного или диаметр круглого фундамента; kc и km — коэффициенты, принимаемые по табл. 5.17 и 5.18; n — число слоев, различающихся по сжимаемости в пределах расчетной толщины слоя H ; ki и ki-1 — коэффициенты, определяемые по табл. 5.19 в зависимости от формы фундамента, соотношения сторон прямоугольного фундамента и относительной глубины, на которой расположены подошвы и кровля i -го слоя (соответственно ζi = 2zi/b и ζi-1 = 2zi-1/b) ; Ei — модуль деформации i -го слоя грунта.
Формула (5.61) служит для определения средней осадки основания, загруженного равномерно распределенной по ограниченной площади нагрузкой. Эту формулу допускается применять для определения осадки жестких фундаментов.
ТАБЛИЦА 5.17. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА kc
| Относительная толщина слоя ζ´ = 2H/b | kс |
| 0 ζ´ ≤ 0,5 | 1,5 |
| 0,5 ζ´ ≤ l | 1,4 |
| 1 ζ´ ≤ 2 | 1,3 |
| 2 ζ´ ≤ 3 | 1,2 |
| 3 ζ´ ≤ 5 | 1,1 |
| ζ´ > 5 | 1,0 |
ТАБЛИЦА 5.18. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА km
| Ширина фундамента, м | km при среднем значении Е , МПа | |
| b > 10 10 ≤ b ≤ 15 b > 15 | 1 1 1 | 1 1,35 1,5 |
Расчетная толщина линейно-деформируемого слоя H (см. рис. 6.27) принимается до кровли малосжимаемого грунта (см. п. 5.1), а при ширине (диаметре) фундамента b > 10 м и среднем значении модуля деформации грунтов основания E > 10 МПа вычисляется по формуле
где H0 и ψ — принимаются соответственно равными для оснований, сложенных пылевато-глинистыми грунтами 9 м и 0,15, а сложенных песчаными грунтами 6 м и 0,1; kp — коэффициент, принимаемый; kp = 0,8 при среднем давлении под подошвой фундамента p = 100 кПа; kp = 1,2 при р = 500 кПа; при промежуточных значениях — по интерполяции.
Если основание сложено и пылевато-глинистыми, и песчаными грунтами, значение Н определяется по формуле
где Нs — толщина слоя, вычисленная по формуле (5.62) в предположении, что основание сложено только песчаными грунтами; hci — суммарная толщина слоев пылевато-глинистых грунтов в пределах от подошвы фундамента до глубины Hci равной значению Н , вычисленному по формуле (5.62) в предположении, что основание сложено только пылевато-глинистыми грунтами.
ТАБЛИЦА 5.19. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА k
| ζ = 2z/b | k для фундаментов | |||||||
| круглых | прямоугольных с соотношением сторон η = l/b | ленточных ( η ≥ 10) | ||||||
| 1 | 1,4 | 1,8 | 2,4 | 3,2 | 5 | |||
| 0,0 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 0,4 | 0,090 | 0,100 | 0,100 | 0,100 | 0,100 | 0,100 | 0,100 | 0,104 |
| 0,8 | 0,179 | 0,200 | 0,200 | 0,200 | 0,200 | 0,200 | 0,200 | 0,208 |
| 1,2 | 0,266 | 0,299 | 0,300 | 0,300 | 0,300 | 0,300 | 0,300 | 0,311 |
| 1,6 | 0,348 | 0,380 | 0,394 | 0,397 | 0,397 | 0,397 | 0,397 | 0,412 |
| 2,0 | 0,411 | 0,446 | 0,472 | 0,482 | 0,486 | 0,486 | 0,486 | 0,511 |
| 2,4 | 0,461 | 0,499 | 0,538 | 0,556 | 0,565 | 0,567 | 0,567 | 0,605 |
| 2,8 | 0,501 | 0,542 | 0,592 | 0,618 | 0,635 | 0,640 | 0,640 | 0,687 |
| 3,2 | 0,532 | 0,577 | 0,637 | 0,671 | 0,696 | 0,707 | 0,709 | 0,763 |
| 3,6 | 0,558 | 0,606 | 0,676 | 0,717 | 0,750 | 0,768 | 0,772 | 0,831 |
| 4,0 | 0,579 | 0,630 | 0,708 | 0,756 | 0,796 | 0,820 | 0,830 | 0,892 |
| 4,4 | 0,596 | 0,650 | 0,735 | 0,789 | 0,837 | 0,867 | 0,883 | 0,949 |
| 4,8 | 0,611 | 0,668 | 0,759 | 0,819 | 0,873 | 0,908 | 0,932 | 1,001 |
| 5,2 | 0,624 | 0,683 | 0,780 | 0,834 | 0,904 | 0,948 | 0,977 | 1,050 |
| 5,6 | 0,635 | 0,697 | 0,798 | 0,867 | 0,933 | 0,981 | 1,018 | 1,095 |
| 6,0 | 0,645 | 0,708 | 0,814 | 0,887 | 0,958 | 1,011 | 1,056 | 1,138 |
| 6,4 | 0,653 | 0,719 | 0,828 | 0,904 | 0,980 | 1,031 | 1,090 | 1,178 |
| 6,8 | 0,661 | 0,728 | 0,841 | 0,920 | 1,000 | 1,065 | 1,122 | 1,215 |
| 7,2 | 0,668 | 0,736 | 0,852 | 0,935 | 1,019 | 1,088 | 1,152 | 1,251 |
| 7,6 | 0,674 | 0,744 | 0,863 | 0,948 | 1,036 | 1,109 | 1,180 | 1,285 |
| 8,0 | 0,679 | 0,751 | 0,872 | 0,960 | 1,051 | 1,128 | 1,205 | 1,316 |
| 8,4 | 0,684 | 0,757 | 0,881 | 0,970 | 1,065 | 1,146 | 1,229 | 1,347 |
| 8,8 | 0,689 | 0,762 | 0,888 | 0,980 | 1,078 | 1,162 | 1,251 | 1,376 |
| 9,2 | 0,693 | 0,768 | 0,896 | 0,989 | 1,089 | 1,178 | 1,272 | 1,404 |
| 9,6 | 0,697 | 0,772 | 0,902 | 0,998 | 1,100 | 1,192 | 1,291 | 1,431 |
| 10,0 | 0,700 | 0,777 | 0,908 | 1,005 | 1,110 | 1,205 | 1,309 | 1,456 |
| 11,0 | 0,705 | 0,786 | 0,922 | 1,022 | 1,132 | 1,233 | 1,349 | 1,506 |
| 12,0 | 0,710 | 0,794 | 0,933 | 1,037 | 1,151 | 1,257 | 1,384 | 1,550 |
Примечание. При промежуточных значениях ζ и η коэффициент k определяется по интерполяции.
Значение Н , найденное по формулам (5.62) и (5.63), должно быть увеличено на толщину слоя грунта с модулем деформации E H и толщина его не превышает 0,2 H . При большей толщине слоя такого грунта, а также если лежащие выше слои имеют модуль деформации E р = 0,3 МПа, если плита опирается на слой песка толщиной 5 м с модулем деформации E = 30 МПа, который подстилается моренным суглинком, имеющим Е = 40 МПа.
Решение. Расчетную толщину слои определяем но формуле (5.62) для двух случаев: основание сложено только песчаными и только пылевато-глинистыми грунтами (при р = 0,3 МПа коэффициент kр = 1):
Тогда по формуле (5.63)
H = 8 + 7/3 = 10,3 м ≈ 10 м.
При ζ´ = 2 · 10/20 = 1 по табл. 5.17 kc = 1,4; при Е > 10 МПа и b > 15 м по табл. 5.18 коэффициент km = 1,5.
Определяем коэффициенты ki по табл. 5.19, учитывая, что η = 100/20 = 5:
Тогда по формуле (5.61)

Осадки центра, середин сторон и угловых точек прямоугольной площади размером b×l при действии на нее равномерного давления р определяются по формуле [2]:
где E — модуль деформации грунта основания, принимаемый средним в пределах сжимаемой толщи; k´ = k0 коэффициент, принимаемый по табл. 5.20 для центра прямоугольника; k´ = k1 — то же, для середины большей стороны; k´ = k2 — то же, для середины меньшей стороны; k´ = k3 — то же, для угловой точки.
Осадки поверхности основания при действии на него равномерного давления р по круглой площадке радиусом r на расстоянии R от центра этой площадки также можно определить по формуле (5.64), в которой коэффициент k´ = kr принимается по табл. 5.21 [2]. Указанным способом допускается определять осадки поверхности основания за пределами жесткого круглого фундамента.
Влияние на осадку рассчитываемого фундамента других фундаментов, нагрузок на полы и т.п. может быть оценено по формуле (5.64) с использованием схемы фиктивных фундаментов аналогично определению напряжений в основании методом угловых точек либо с помощью ЭВМ по стандартной программе. Дополнительную осадку рассчитываемого фундамента от влияния других фундаментов допускается принимать равной дополнительной осадке его центра.
ТАБЛИЦА 5.20. ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ k0, k1, k2, k3
| η | ζ´ = 2H/b | k0 | k1 | k2 | k3 | η | ζ´ = 2H/b | k0 | k1 | k2 | k3 |
| 1 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,236 0,464 0,701 0,801 0,892 0,928 0,955 | 0,045 0,109 0,236 0,436 0,482 0,564 0,601 0,628 | 0,045 0,109 0,236 0,436 0,482 0,564 0,601 0,628 | 0,024 0,056 0,115 0,231 0,305 0,380 0,416 0,444 | 3 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,801 1,019 1,238 1,338 1,420 | 0,045 0,109 0,227 0,464 0,655 0,855 0,955 1,037 | 0,045 0,107 0,225 0,400 0,510 0,656 0,742 0,815 | 0,024 0,056 0,115 0,231 0,325 0,460 0,545 0,617 |
| 1,5 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,773 0,910 1,037 1,092 1,137 | 0,045 0,109 0,236 0,446 0,564 0,682 0,737 0,783 | 0,045 0,108 0,231 0,404 0,508 0,617 0,669 0,712 | 0,024 0,056 0,115 0,231 0,323 0,426 0,478 0,518 | 5 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,454 0,801 1,028 1,310 1,456 1,592 | 0,045 0,109 0,227 0,464 0,655 0,919 1,065 1,192 | 0,045 0,107 0,225 0,400 0,511 0,656 0,752 0,852 | 0,024 0,056 0,115 0,231 0,326 0,462 0,555 0,652 |
| 2 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,792 0,974 1,128 1,201 1,265 | 0,045 0,109 0,227 0,464 0,610 0,755 0,837 0,883 | 0,044 0,107 0,225 0,403 0,514 0,641 0,708 0,762 | 0,024 0,056 0,115 0,231 0,324 0,448 0,512 0,565 | 10 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,801 1,028 1,319 1,492 1,702 | 0,045 0,109 0,227 0,464 0,655 0,928 1,110 1,310 | 0,045 0,107 0,225 0,400 0,511 0,658 0,756 0,858 | 0,024 0,056 0,115 0,231 0,326 0,463 0,558 0,659 |
ТАБЛИЦА 5.21. ЗНАЧЕНИЕ КОЭФФИЦИЕНТА kr
| ζ´ = H/r | kr при ρ = R/r | |||||||||||
| 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 2 | 2,5 | 3 | 4 | 5 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,25 | 0,12 | 0,12 | 0,12 | 0,12 | 0,05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,5 | 0,24 | 0,24 | 0,23 | 0,22 | 0,11 | 0,01 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,75 | 0,35 | 0,35 | 0,34 | 0,29 | 0,16 | 0,03 | 0,01 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,45 | 0,44 | 0,42 | 0,35 | 0,21 | 0,07 | 0,02 | 0 | 0 | 0 | 0 | 0 |
| 1,5 | 0,58 | 0,57 | 0,53 | 0,45 | 0,28 | 0,13 | 0,07 | 0,02 | 0 | 0 | 0 | 0 |
| 2 | 0,65 | 0,64 | 0,60 | 0,52 | 0,34 | 0,17 | 0,10 | 0,04 | 0,01 | 0 | 0 | 0 |
| 3 | 0,74 | 0,73 | 0,68 | 0,59 | 0,41 | 0,23 | 0,16 | 0,08 | 0,04 | 0,02 | 0 | 0 |
| 5 | 0,81 | 0,79 | 0,74 | 0,66 | 0,47 | 0,30 | 0,22 | 0,13 | 0,09 | 0,06 | 0,02 | 0,01 |
| 7 | 0,84 | 0,82 | 0,77 | 0,69 | 0,50 | 0,33 | 0,24 | 0,15 | 0,11 | 0,08 | 0,04 | 0,02 |
| 10 | 0,85 | 0,83 | 0,79 | 0,71 | 0,52 | 0,35 | 0,27 | 0,18 | 0,13 | 0,10 | 0,06 | 0,04 |
| ∞ | 0,91 | 0,89 | 0,84 | 0,76 | 0,58 | 0,40 | 0,32 | 0,23 | 0,18 | 0,15 | 0,11 | 0,09 |
ТАБЛИЦА 5.22. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА ω
| Форма загруженной площади | η | ω для определения | |||
| осадки равномерно загруженной площади | осадки абсолютно жесткого фундамента ωconst | ||||
| в угловой точке ωc | в центре ω0 | в средней ωm | |||
| Прямоугольная | 1 | 0,5 ω0 | 1,12 | 0,95 | 0,88 |
| 1,5 | 1,36 | 1,15 | 1,08 | ||
| 2 | 1,53 | 1,30 | 1,22 | ||
| 3 | 1,78 | 1,53 | 1,44 | ||
| 4 | 1,96 | 1,70 | 1,61 | ||
| 5 | 2,10 | 1,83 | 1,72 | ||
| 6 | 2,23 | 1,96 | 1,83 | ||
| 7 | 2,33 | 2,04 | 1,92 | ||
| 8 | 2,42 | 2,12 | 2,00 | ||
| 9 | 2,49 | 2.19 | 2,06 | ||
| 10 | 2,53 | 2,25 | 2,12 | ||
| Круглая | – | 0,64 | 1,00 | 0,85 | 0,79 |
Определение осадки путем непосредственного применения теории линейно-деформируемой среды. Для предварительной оценки осадок фундаментов допускается пользоваться формулой
где ω — коэффициент, принимаемый по табл. 5.22; v — коэффициент Пуассона.
Во всех случаях формула (5.65) приводит к преувеличению расчетных осадок (по сравнению с методами, рекомендуемыми нормами). Достаточно удовлетворительные результаты эта формула дает при ширине фундамента b η = l/b
Сорочан Е.А. Основания, фундаменты и подземные сооружения
Источник