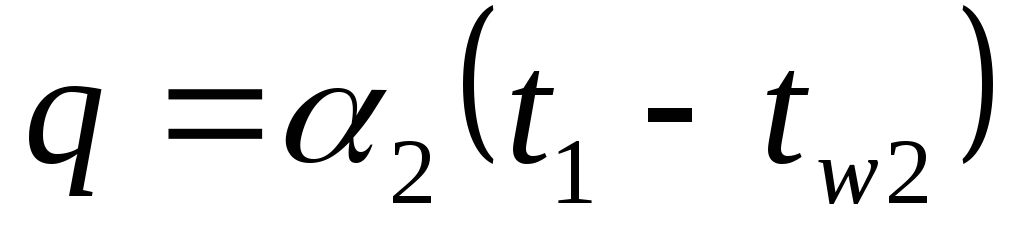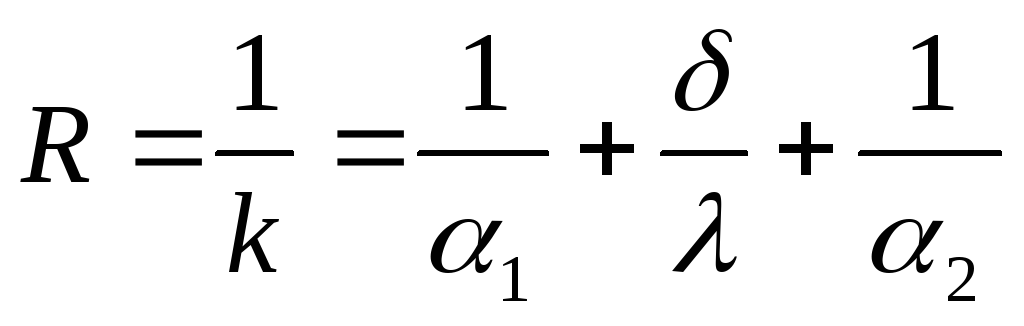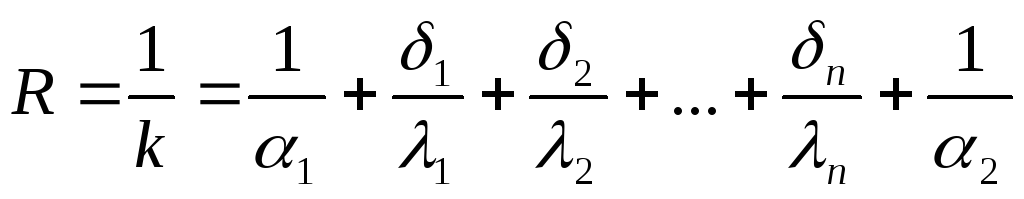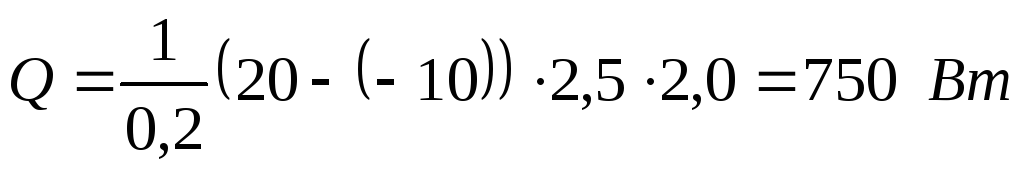Определить тепловой поток через бетонную стену здания

TOA_studentam / Лекции / 1.3 Теплопроводность при стационарном режиме

При установившемся, или стационарном тепловом режиме температура тела во времени остается постоянной. При этом полученное нами дифференциальное уравнение теплопроводности упрощается:

Если внутренние источники теплоты отсутствуют, то уравнение еще упростится:

Рассмотрим теплопроводность в телах простейшей геометрической формы.

Передача теплоты через плоскую стенку.

Рассмотрим передачу теплоты через плоскую стенку (рис. 1.3) в случае, когда заданы граничные условия первого рода. Стенка толщиной δ имеет постоянный коэффициент теплопроводности λ. На наружных поверхностях стенки поддерживаются постоянные температуры t₁ и t₂. При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки. Направим ось х, как показано на рис. 1.3, тогда для осей y и z справедливо:

Рис. 1.3.1 Передача теплоты

через плоскую стенку

связи с этим температура будет функцией только координаты х, а дифференциальное уравнение для этого случая будет иметь вид:

Граничные условия в рассматриваемой передаче запишем следующим образом:

Дифференциальное уравнение вместе с граничными условиями дают полную математическую формулировку поставленной задачи.

В результате решения этой задачи должно быть найдено распределение температуры в плоской стенке t = f(x), и получена формула для определения плотности теплового потока.

Закон распределения температуры в плоской стенке найдем выполнив интегрирование уравнения:

Таким образом, при постоянном коэффициенте теплопроводности, температура в стенке изменяется по линейному закону.

Константы определим из граничных условий:

при х = δ, t = t₂ =>

Для определения количества теплоты, проходящего через единицу поверхности стенки в единицу времени в направлении оси х, воспользуемся законом Фурье, согласно которому:

и , получим:

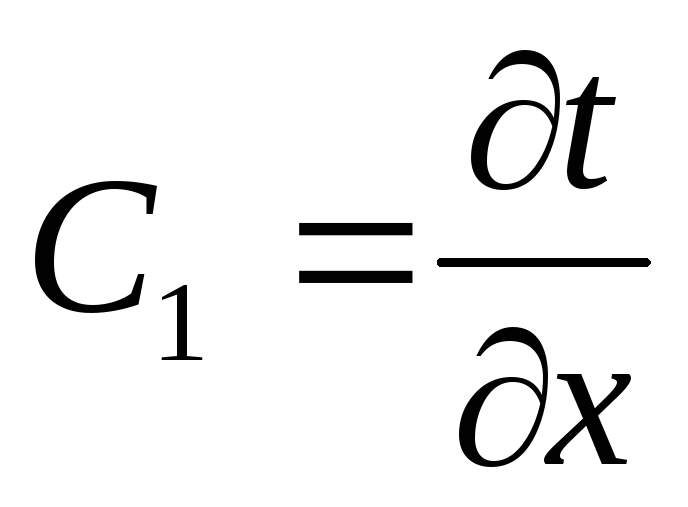
Из полученного уравнения следует, что количество теплоты, проходящее через единицу поверхности стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности λ и разности температур, и обратно пропорционально толщине стенке δ. Отметим, что тепловой поток определяется не абсолютным значением температур, а их разностью, которую называют температурным напором.

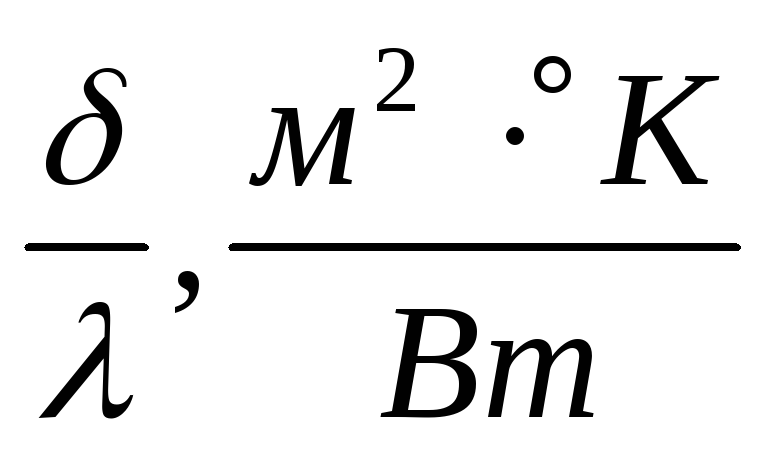
Отношение называется тепловой проводимостью стенки, а обратная величина – тепловым (термическим) сопротивлением стенки, которое представляет собой падение температуры в стенке на единицу плотности теплового потока.

Зная плотность теплового потока, легко вычислить общее количество теплоты Q, которое передается через стенку площадью F за промежуток времени τ:

Используя, полученные выражения, можем записать температурное поле в виде:

В действительности коэффициент теплопроводности λ является переменной величиной. Рассмотрим случай, когда коэффициент теплопроводности является функцией температуры λ = λ(t).

Для многих материалов зависимость коэффициента теплопроводности от температуры близка к линейной:

где – значение коэффициента теплопроводности при 0°С.

На основании закона Фурье, запишем:

Выполнив интегрирование 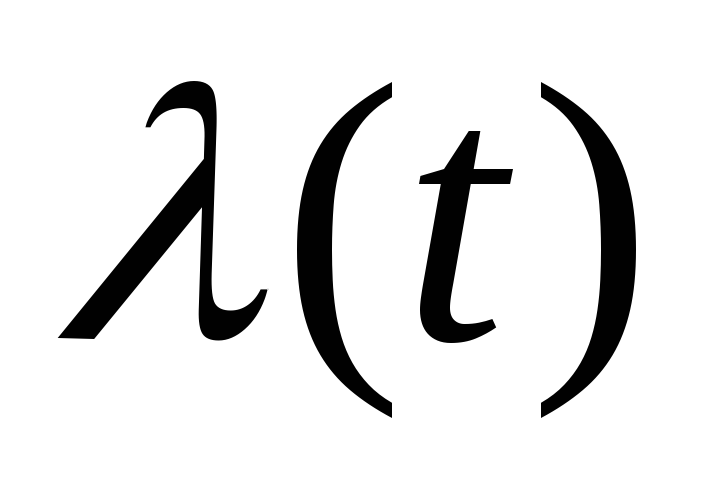, найдем среднеинтегральное значение коэффициента теплопроводности:

Тогда плотность теплового потока можно вычислить по формуле:

Таким образом, если коэффициент теплопроводности зависит от температуры, то для вычисления теплового потока можно использовать среднеинтегральное значение теплопроводности в заданном интервале температур.

Передача теплоты через многослойную плоскую стенку.

Рассмотрим теплопроводность многослойной плоской стенки, состоящей из n однородных слоев. Примем, что контакт между слоями полный и температура на соприкасающихся поверхностях двух слоев одинакова.

При стационарном режиме тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, один и тот же:

При заданных температурах на внешних поверхностях многослойной стенки, размерах слоев и соответствующих коэффициентах теплопроводности, можно составить систему уравнений:

Определив температурные напоры в каждом слое и выполнив суммирование, получим:

Отсюда можно получить плотность теплового потока:

Величина в знаменателе, равная сумме термических сопротивлений всех n слоев стенки, называется полным термическим сопротивлением многослойной стенки.

При сравнении переноса теплоты через многослойную стенку и стенку из однородного материала удобно ввести в рассмотрение эквивалентный коэффициент теплопроводности. Он равен коэффициенту теплопроводности однородной стенки, толщина которой δ равна толщине многослойной стенки , а термическое сопротивление равно термическому сопротивлению рассматриваемой многослойной стенки, т.е.

Из полученного уравнения следует, что эквивалентный коэффициент теплопроводности зависит не только от теплофизических свойств слоев, но и от их толщины. Температуры на границах соприкосновения двух соседних слоев равны:

Для многослойной стенки в целом температурная кривая представляет собой ломанную линию.

Передача теплоты от одной среды (жидкости или газа) к другой через разделяющую их стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости (газа) к стенке, теплопроводность в стенке и теплоотдачу от стенки к более холодной жидкости (газу).

Рис. 1.3.2 Теплопередача через плоскую стенку

ассмотрим теплопередачу от одной жидкости к другой через однослойную плоскую стенку (рис. 1.3.2). Пусть плоская стенка имеет толщину δ. Заданы коэффициент теплопроводности стенки λ, температуры окружающих сред, а также коэффициенты теплоотдачи. Будем считать, что все эти величины не меняются вдоль поверхности. Это позволяет рассматривать изменение температур стенки и жидкости только в направлении, перпендикулярном плоскости стенки.

При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности стенки.

Плотность теплового потока от горячей жидкости к стенке определяется уравнением:

Та же плотность теплового потока, обусловленная теплопроводностью, определится как:

Та же плотность теплового потока от второй поверхности стенки к холодной жидкости за счет теплоотдачи:

Определив из этих выражений температурный напор и выполнив суммирование, получим:

Отсюда плотность теплового потока:

Величина k имеет такую же размерность, что и α , и называется коэффициентом теплопередачи. Коэффициент теплопередачи численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.

Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи:

Термическое сопротивление теплопередачи складывается из термического сопротивления теплоотдачи от горячей жидкости к поверхности стенки, термического сопротивления теплопроводности стенки и термического сопротивления теплоотдачи от поверхности стенки к холодной жидкости.

Очевидно, что для многослойной стенки термическое сопротивление теплопередачи будет:

Тепловой поток Q, через поверхность стенки F равен:

Температуры поверхности стенки можно найти из уравнений:

Графический метод определения температур.

Рассмотрим графический метод определения температур на поверхности слоев многослойной стенки, в основу которого положено свойство линейной зависимости температурного напора от термического сопротивления стенки:

или для любого слоя:

Такая зависимость дает возможность построить фиктивную стенку, в которой толщины слоев будут пропорциональны соответствующим термическим сопротивлениям, а внешние термические сопротивления теплоотдачи учитываются путем введения двух условных граничных слоев соответствующей толщины. Сущность метода поясним на примере трехслойной стенки (рис. 1.3.3).

Термическое сопротивление теплопередачи через такую стенку равно:

Отложим на оси абсцисс отрезки соответственно равные термическим сопротивлениям перечисленным в формуле. На границах отрезков проведем перпендикуляры. На крайних перпендикулярах отложим в произвольном масштабе температуры жидкостей и соединим полученные точки прямой. Эта прямая отсечет на оставшихся перпендикулярах температуры на

Рис. 1.3.3 Теплопередача через многослойную стенку

поверхности слоев стенки. Из подобия треугольников АВС и abc следует, что:

или

Выполним некоторые преобразования:

Из полученных соотношений следует:

Аналогично доказывается, что и другие отрезки соответствуют температурам на поверхности слоев стенки.

Определить тепловой поток через бетонную стену здания толщиной 200 мм, высотой 2,5 м и длиной 2 м. Если температуры на поверхности стены: t₁ = 20°C; t₂ = —10°C, а коэффициент теплопроводности бетона λ = 1 Вт/(м·°К).

Так как процесс стационарный и внутренних источников тепла нет, то можно воспользоваться формулой, выведенной нами ранее:

На реке лед толщиной 300 мм покрыт слоем снега в 200 мм. Температура воздуха -15˚С. Коэффициент теплопроводности льда – 2,23 Вт/(м∙К), коэффициент теплопроводности снега – 0,46 Вт/(м∙К). Найти плотность теплового потока и температуру на границе льда и снега.

Источник