- Онлайн калькулятор. Площадь цилиндра.
- Найти площадь поверхности цилиндра
- Ввод данных в калькулятор для вычисления площади цилиндра
- Дополнительные возможности калькулятора вычисления площади цилиндра
- Теория. Площадь поверхности цилиндра
- Онлайн калькулятор площади цилиндра. Как узнать площадь цилиндра.
- Калькулятор онлайн расчета боковой и полной площади поверхности цилиндра с отображением формул и подробным решением.
- Площадь поверхности цилиндра: онлайн-калькулятор
- Нахождение площади поверхности цилиндра. Онлайн-калькулятор
- Площадь поверхности цилиндра
- Боковая поверхность цилиндра
- Площадь полной поверхности цилиндра
- Примеры расчета площади поверхности цилиндра
Онлайн калькулятор. Площадь цилиндра.
Используя этот онлайн калькулятор, вы сможете найти площадь боковой поверхности цилиндра, а также площадь полной поверхности цилиндра.
Воспользовавшись онлайн калькулятором для вычисления площади поверхности цилиндра, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь поверхности цилиндра
Введите значение радиуса цилиндра и его высоты
| R = |
| h = |
Ввод данных в калькулятор для вычисления площади цилиндра
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади цилиндра
- Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.
Теория. Площадь поверхности цилиндра
— геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями (основаниями), пересекающими её.
Цилиндр называется круговым, если его основание – круг. Расстояние между основаниями – высота цилиндра.
Формулы для вычисления площади боковой поверхности цилиндра
Формулы для вычисления площади полной поверхности цилиндра
S = 2 π R h + 2 π R 2 = 2 π R ( R + h )
где S — площадь,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Источник
Онлайн калькулятор площади цилиндра. Как узнать площадь цилиндра.
Для того что бы вычислить площадь цилиндра необходимо знать его высоту и радиус или диаметр. Если нам известны указанные величины, для нас не составит труда вычислить площадь.
Полная площадь цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
Площадь боковой поверхности цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
Где S – площадь, R – радиус, D – диаметр, h — высота, π – число Пи которое всегда примерно равно 3,14.
Источник
Калькулятор онлайн расчета боковой и полной площади поверхности цилиндра с отображением формул и подробным решением.
Калькулятора онлайн рассчитывает площадь площадь боковой и полной поверхности цилиндра и выводит формулы с подробным решением:
- площадь боковой Sside поверхности круглого цилиндра равна произведению длины окружности основания на высоту;
- площадь полной Sfull поверхности круглого цилиндра равна сумме площадей боковой поверхности круглого цилиндра и удвоенной площади основания. Основание круглого цилиндра есть круг и его площадь вычисляется по формуле площади круга .
| Исходные данные: | Решение: | ||
| Радиус основания | r = |  | |
| Высота цилиндра | h = | ||
I. Для справки:
1. Цилиндрической поверхностью называется поверхность, образуемая прямой, сохраняющей одно и тоже направление и пересекающей направляющую линию. Цилиндр — круговой если в основании его лежит круг.
2. Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
3. Площадь поверхности — аддитивная числовая характеристика поверхности.
Источник
Площадь поверхности цилиндра: онлайн-калькулятор
Высчитать площадь полной поверхности цилиндра с помощью нашего сервиса легко. Удобный интерфейс с чертежом иллюстрирует формулу и наглядно показывает, какие данные необходимы для решения задачи.
Все преобразования происходят автоматически и видны в расчетах. Вам остается только ввести известные величины. Сервис работает без регистрации и оплаты. Программа позволяет получить ход вычислений и быстрый ответ, что очень важно на экзаменах, зачетах, контрольных.
- Введите данные задачи в соответствующие окна.
- Установите нужные единицы измерения. Отправьте задачу на расчет кнопкой «Найти».
- Получите решение и ответ.
Нахождение площади поверхности цилиндра. Онлайн-калькулятор
Программа рассчитывает площадь поверхности цилиндра по формуле:
где R – радиус основания,
h – высота фигуры.
В разделе с калькуляторами собраны расчеты и для других фигур. Для решения составного задания ищите необходимые программы. Вычисления не ограничиваются в количестве. Отсылайте нужное число запросов для усвоения материала. Автоматизированные подсчеты с пошаговыми действиями помогают самостоятельно изучать тему и запоминать алгоритм.
- Школьникам. Самостоятельная подготовка к урокам становится проще и быстрее, когда есть возможность свериться с ответом. Кроме этого родителям больше не понадобится вникать в тему, чтобы проверить подготовку ребенка.
- Студентам. Получить проходной балл можно благодаря автоматизированному подсчету.
- Преподавателям. За счет экономии времени на проверке расчетов можно составить больше индивидуальных заданий и не пересчитывать их вручную.
Если возникли вопросы по теме, обратитесь к консультанту. Наш сотрудник поможет найти преподавателя по вашему запросу. Услуги по объяснению непонятной темы, решению задач и онлайн-помощи стоят недорого.
Источник
Площадь поверхности цилиндра
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Боковая поверхность цилиндра
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
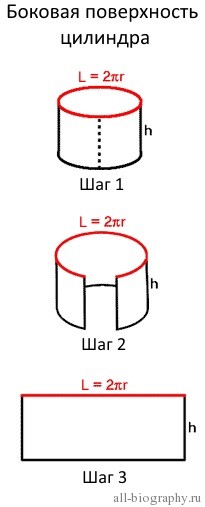
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Sбок. = 2 * 3,14 * 2 * 3
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
S = 226,08 + 150,72
Площадь поверхности цилиндра равна 376,8.
3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.
Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:
Значение радиуса получаем из формулы: d = 2r
Источник