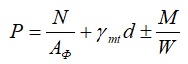Расчет фундамента ленточного или под колонну

6.5. РАСЧЕТ ПЛИТНЫХ И ЛЕНТОЧНЫХ ФУНДАМЕНТОВ ПОД КОЛОННЫ

6.5.1. Общие положения

Расчет ленточных и плитных фундаментов, работающих на изгиб, проводится с учетом совместной работы конструкции и грунтового основания согласно теории конструкций на упругом основании. В этом случае предположение о линейном распределении реактивных давлений уже не может рассматриваться как достаточно точное, так как изгиб конструкции изменяет распределение этих давлений и, следовательно, отражается и на усилиях в балках и плитах. Линейное распределение давлений используется лишь для предварительного определения сечений конструкций.

6.5.2. Предварительное назначение размеров сечений

Предварительное назначение размеров сечений рассмотрим на примере ленточного фундамента под колонны, исходя из схемы линейного распределения реактивных давлений. Изгибающие моменты в каждом сечении ленты определяются по формуле

где M_l — момент в данном сечении от площади эпюры реактивных давлений, расположенной левее данного сечения; ΣP_il_i — сумма моментов для данного сечения от нагрузок, передаваемых колоннами, расположенными левее сечения (здесь Р_i — нагрузка от колонны i ; l_i —расстояние от колонны до сечения); ΣМ_i — сумма внешних моментов, передаваемых колоннами, расположенными левее данного сечения.

За положительное направление моментов принимается направление по часовой стрелке.

Таким образом, изгибающие моменты определяются простейшим способом по схеме статически определяемой балки. Не рекомендуется пользоваться расчетом статически неопределимой неразрезной балки, нагруженной трапецеидальной эпюрой давлений, при котором опорные реакции оказываются отличными от расчетных нагрузок, передаваемых на балку колоннами; кроме того, такой расчет сложнее. Использование схемы неразрезной балки оправдано лишь в случае, если жесткость верхнего строения очень велика и не позволяет смещаться опорным точкам колонн нелинейно относительно друг друга. В этом случае учитывается перераспределение внешней нагрузки по колоннам исходя из учета жесткости верхнего строения.

6.5.3. Расчет фундаментных балок и плит как конструкций на упругом основании

Для учета влияния изгиба на распределение реактивных давлений используется одно из двух предположений.

1. Основание работает согласно гипотезе коэффициента постели (Винклера). Эта гипотеза предполагает, что осадка какой-либо точки (элемента) поверхности основания s пропорциональна давлению р , приложенному в той же точке, т.е. что p = k_ss . Коэффициент k_s , Па/м, называется коэффициентом постели. Осадка данной точки (элемента) зависит только от давления, приложенного в этой точке, и не зависит от давлений, действующих по соседству (рис. 6.32, а).

2. Основание работает как среда, к которой применимы формулы теории упругости, связывающие напряжения и осадки. Грунт принимается за однородное упругое тело, бесконечно простирающееся вниз и в стороны и ограниченное сверху плоскостью (упругое полупространство), а соответствующее предположение называется гипотезой упругого полупространства. Поверхность упругого полупространства деформируется не только непосредственно под нагрузкой, но и по соседству с ней (рис. 6.32, б). Деформационные свойства грунта характеризуются в основном модулем деформации Е₀ , МПа.

Согласно гипотезе коэффициента постели, грунт лишен распределительной способности, т.е. деформации соседних с нагрузкой элементов поверхности грунта отсутствуют. Коэффициент постели для данного типа основания предполагается величиной, не зависящей от площади фундамента (в действительности — зависит).

В гипотезе упругого полупространства распределительная способность преувеличена. Модуль деформации является характеристикой, представляющей одновременно как упругие, так и остаточные деформации. При многократном приложении нагрузки остаточные деформации исчезают, модуль общей деформации Е₀ переходит в модуль упругости Е , значительно больший, чем Е₀ , При ширине фундамента примерно от 70 см до 7 м значение модуля деформации меняется незначительно. При превышении ширины 7 м модуль деформации заметно возрастает.

6.5.4. Связь между расчетными значениями модуля деформации и коэффициента постели

Между расчетными значениями модуля деформации Е₀ и коэффициентом постели, исходя из приравнивания осадок, вычисленных по той и другой гипотезе, устанавливается связь

Значение k₀ определяется по рис. 6.33 в зависимости от отношения сторон прямоугольного фундамента α, его опорной площади А и коэффициента Пуассона грунта ν₀ , принимаемого для песков ν₀ = 0,3, для суглинков и супесей ν₀ = 0,35, для глин ν₀ = 0,4.

Осадки жесткого прямоугольного фундамента на однородном основании определяются по формуле

где Р — суммарная центрированная нагрузка на фундамент.

Осадки жесткой плиты лишь немного меньше (на 7 %) средних осадок гибкой плиты при равномерной нагрузке.

Расчеты по обеим гипотезам, даже при использовании формулы (6.126), дают, как правило, различные результаты в отношении изгибающих моментов в конструкции и ее изгиба. Только для узких балок при α ≥ 10 можно подобрать отличное от определяемого формулой (6.127) значение коэффициента постели, при котором результаты расчета будут близки. Однако при равномерной нагрузке или при нагрузке, приближающейся к ней, получить близкие результаты расчета при любом соотношении между E₀ и k невозможно. Формула соотношения между Е₀ и k , для узких балок шириной В имеет вид:

Гибкие фундаменты в настоящее время рассчитываются преимущественно по гипотезе упругого полупространства. Этот расчет при фундаментах большой опорной площади, в десятки или сотни квадратных метров, дает, однако, преувеличенное значение осадки, изгиба и изгибающих моментов, так как гипотеза игнорирует уплотнение грунта с глубиной, вызванное действием его собственного веса. Кроме того, при больших опорных площадях грунт под фундаментом сжимается в основном без возможности бокового расширения, что не учитывается при опытном определении модуля деформации штампом.

Чтобы приблизить расчетные условия к действительным, при больших опорных площадях используют схему, согласно которой основание представляет собой сжимаемый слой, подстилаемый несжимаемым основанием. Удобно также использовать схему однородного полупространства с повышенным модулем деформации так, чтобы расчет по этой схеме давал значение, равное ожидаемой осадке.

Сорочан Е.А. Основания, фундаменты и подземные сооружения

Источник

Онлайн калькулятор расчета размеров, арматуры и количества бетона монолитного ленточного фундамента

Информация по назначению калькулятора

Онлайн калькулятор монолитного ленточного фундамента предназначен для расчетов размеров, опалубки, количества и диаметра арматуры и объема бетона, необходимого для обустройства данного типа фундамента. Для определения подходящего типа фундамента, обязательно обратитесь к специалистам.

Л енточный фундамент представляет собой монолитную замкнутую железобетонную полосу, проходящую под каждой несущей стеной строения, распределяя тем самым нагрузку по всей длине ленты. Предотвращает проседание и изменение формы постройки вследствие действия сил выпучивания почвы. Основные нагрузки сконцентрированы на углах. Является самым популярным видом среди других фундаментов при строительстве частных домов, так как имеет лучшее соотношение стоимости и необходимых характеристик.

С уществует несколько видов ленточных фундаментов, такие как монолитный и сборный, мелкозаглубленный и глубокозаглубленный. Выбор зависит от характеристик почвы, предполагаемой нагрузки и других параметров, которые необходимо рассматривать в каждом случае индивидуально. Подходит практически для всех типов построек и может применяться при устройстве цокольных этажей и подвалов.

П роектирование фундамента необходимо осуществлять особенно тщательно, так как в случает его деформации, это отразится на всей постройке, а исправление ошибок является очень сложной и дорогостоящей процедурой.

Д алее представлен полный список выполняемых расчетов с кратким описанием каждого пункта.

Источник

buildingbook.ru

Информационный блог о строительстве зданий

• Home
• /
• Железобетонные конструкции
• /
• Конструкции зданий и сооружений
• /
• Расчёт столбчатого фундамента под колонну при действии вертикальной нагрузки и момента в одном направлении

Расчёт столбчатого фундамента под колонну при действии вертикальной нагрузки и момента в одном направлении

В этой статье рассмотрим расчёт фундамента под колонну по 1-му предельному состоянию при нагружении фундамента вертикальной нагрузкой и горизонтальной нагрузкой с изгибающим моментом, действующими в одной плоскости.

Исходные данные

Исходными данными для расчёта фундамента будут нагрузки, приходящие на фундамент от колонны и инженерно-геологические изыскания.

В результате расчёта рамы в расчётной программе получили следующие нагрузки на фундамент:

N=21.3 т (вертикальная нагрузка)

Mx=14.8 т*м (изгибающий момент)

My=0, Qy=0 (Расчёт при действии моментов в 2-х плоскостях рассмотрю отдельно в следующих статьях)

Qx=2.8 т (поперечная нагрузка)

Хочу отметить, что лучше всего проверить 2-а расчётных сочетания:

1. Полная ветровая, снеговая, вес конструкций, равномерно-распределённая
2. Полная ветровая и вес конструкций

Дело в том, что одно из условий расчёта является недопущение отрыва края фундамента от земли и при отсутствии снеговой нагрузки вертикальная нагрузка будет меньше и соответственно меньше сопортивления изгибающему моменту.

Глубина сезонного промерзания – 1,79 м;

Уровень грунтовых вод 1,6 м;

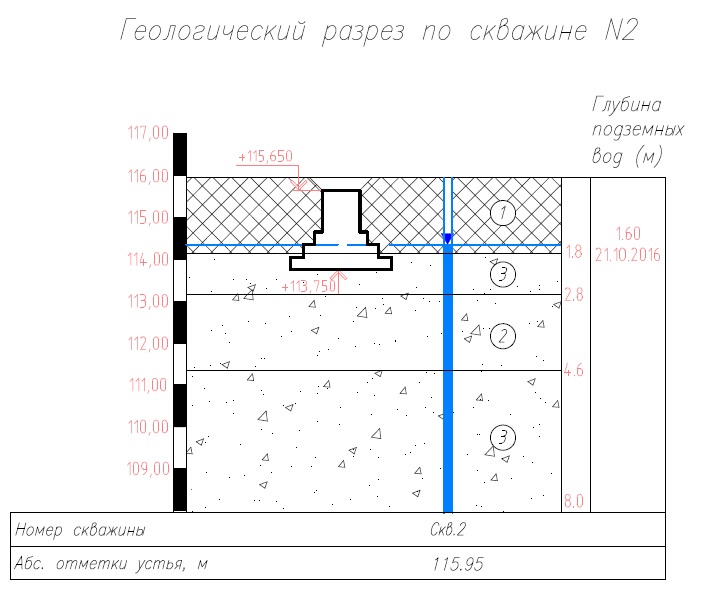
Прочностные свойства грунтов определяются по инженерно-геологическим изысканиям. Для этого ищем инженерно-геологический разрез под нужный фундамент и таблицу с нормативными и расчётными характеристиками грунтов. Для расчёта по 1-му предельному состоянию (расчёту на прочность) необходимы расчётные характеристики при α=0.95 (доверительная вероятность расчётных значений), согласно п.5.3.17 СП 22.13330.2016.

ИГЭ-1 — насыпной грунт — песок разной крупности c вкл. строительного мусора до 15-20%, комки суглика, обломки ж.д. плит (в расчёте не участвует т.к. отметка низа фундамента находится ниже этого слоя грунта);

ИГЭ-2 — песок средней крупности, средней плотности, водонасыщенный: (e=0.65, ρ=1,8 т/м³, Е=30 МПа, ϕ=35°, С=1 кПа).

ИГЭ-3 — песок средней крупности, с редкими прослоями текучей супеси, суглинка, глиниcтый средней плотности, водонасыщенный: (e=0.6, ρ=1,82 т/м³, Е=35 МПа, ϕ=36°, С=1,5 кПа).

Уровень грунтовых вод 1,8 м от уровня земли.

Расчёт фундамента

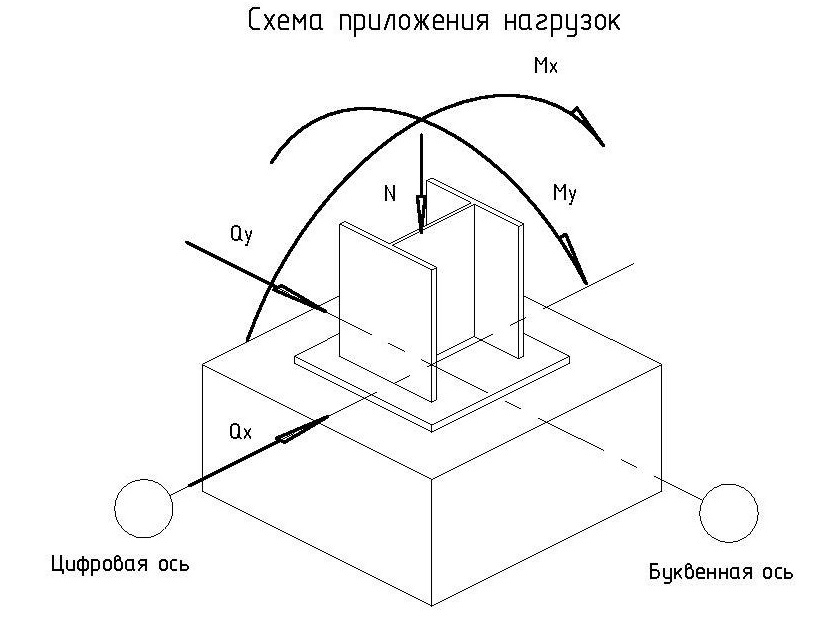
Схема приложения нагрузок на фундамент выглядит следующим образом:

Глубина заложения фундамента

Глубину заложения фундамента определяем в зависимости от максимальной глубины сезонного промерзания, которая дана в отчёте по инженерно-геологическим изысканиям. В моём случае нормативная глубина сезонного промерзания равна d_fn=1,79м.

Расчётная глубина сезонного промерзания вычисляется по формуле 5.4 СП 22.13330.2016

где k_h — коэффициент, учитывающий влияние теплового режима сооружения, принимаемый для наружных фундаментов отапливаемых сооружений — по таблице 5.2 СП 22.13330.2016; для наружных и внутренних фундаментов неотапливаемых сооружений k_h=1,1, кроме районов с отрицательной среднегодовой температурой;

В нашем случае здание неотапливаемое, поэтому

Глубина заложения фундамента должна быть не выше расчётной глубины промерзания (согласно таблице 5.3 СП 22.13330.2016). Для отапливаемых зданий допускается устраивать фундаменты внутри здания (не под наружными стенами) выше глубины промерзания, но должно быть гарантировано, что в холодное время года будет отопление здания. Если же допускается, что здание могут подвергнуть консервации или отключить отопление, тогда и внутренние фундаменты также должны быть заложены на расчётную глубину промерзания.

Предварительные размеры фундамента

Определяем предварительно площадь основания фундамента.

Предварительные размеры фундамента определяем по формуле:

N — вертикальная нагрузка от колонны, которую мы получили при расчёте каркаса здания (N=21,3 т=213 кН);

R₀ – расчётное сопротивление грунта, предназначенное для предварительного расчёта приведены в Приложении Б СП 22.13330.2016 (в нашем случае Таблица Б.2 для песка средней крупности и средней плотности R₀ = 400кПа, для глины и других грунтов см. другие таблицы в приложении Б);

Таблица Б.2 — Расчетные сопротивления R₀ песков

Пески	Значения R0, кПа, в зависимости от плотности сложения песков
плотные	средней плотности
Крупные	600	500
Средней крупности	500	400
Мелкие:
маловлажные	400	300
влажные и насыщенные водой	300	200
Пылеватые:
маловлажные	300	250
влажные	200	150
насыщенные водой	150	100

ȳ — среднее значение удельного веса фундамента и грунта на его обрезах, предварительно принимаемое ȳ=20 кН/м³;

d – глубина заложения фундамента (в нашем случае d=2 м)

+20% т.к. фундамент внецентренно сжатый 0,72 м²

Размеры подошвы фундамента назначаются с шагом 0,3 м, размером не менее 1,5х1,5м (Таблица 4 Пособия по проектированию фундаментов на естественном основании)

Таблица 4 Пособия по проектированию фундаментов на естественном основании

Эскиз фундамента	Модульные размеры фундамента, м, при модуле, равном 0,3
	h	hpl	соответственно hpl			подошвы		подколонника
			h1	h2	h3	квадратной b ´ l	прямоугольной b ´ l	под рядовые колонны bcf ´ lcf	под колонны в температурных швах bcf ´lcf
1,5	0,3	0,3	—	—	1,5´1,5	1,5´1,8	0,6´0,6	0,6´1,8
1,8	0,6	0,3	0,3	—	1,8´1,8	1,8´2,1	0,6´0,9	0,9´2,1
2,1	0,9	0,3	0,3	0,3	2,1´2,1	1,8´2,4	0,9´0,9	1,2´2,1
2,4	1,2	0,3	0,3	0,6	2,4´2,4	2,1´2,7	0,9´1,2	1,5´2,1
2,7	1,5	0,3	0,6	0,6	2,7´2,7	2,4´3,0	0,9´1,5	1,8´2,1
3,0	1,8	0,6	0,6	0,6	3,0´3,0	2,7´3,3	1,2´1,2	2,1´2,1
3,6	—	—	—	—	3,6´3,6	3,0´3,6	1,2´1,5	2,1´2,4
4,2	—	—	—	—	4,2´4,2	3,3´3,9	1,2´1,8	2,1´2,7
Далее с шагом	—	—	—	—	4,8´4,8	3,6´4,2	1,2´2,1	—
	5,4´5,4	3,9´4,5	1,2´2,4	—
0,3 м	—	—	—	—	—	4,2´4,8	1,2´2,7	—
или	—	—	—	—	—	4,5´5,1	—	—
0,6	—	—	—	—	—	4,8´5,4	—	—
—	—	—	—	—	5,1´5,7	—	—
—	—	—	—	—	5,4´6,0	—	—

Предварительно назначаем фундамент 1,5х1,5=2,25 м², что больше предварительного минимума 0,72 м².

Расчёт максимального и минимального краевого давления

Максимальное и минимальное краевое давление находим по формуле 5.11 СП 22.13330.2016

Где N=21,3т=213 кН вертикальная нагрузка от колонны в кН;

А_ф=2,25 м² – площадь фундамента, м²;

γ_mt – средневзвешенное значение удельных весов тела фундамента, грунтов и полов, принимаемое 20 кН/м³;

d=2 – глубина заложения фундамента, м;

M-момент от равнодействующей всех нагрузок, действующий по подошве фундамента в кН*м, находим по формуле:

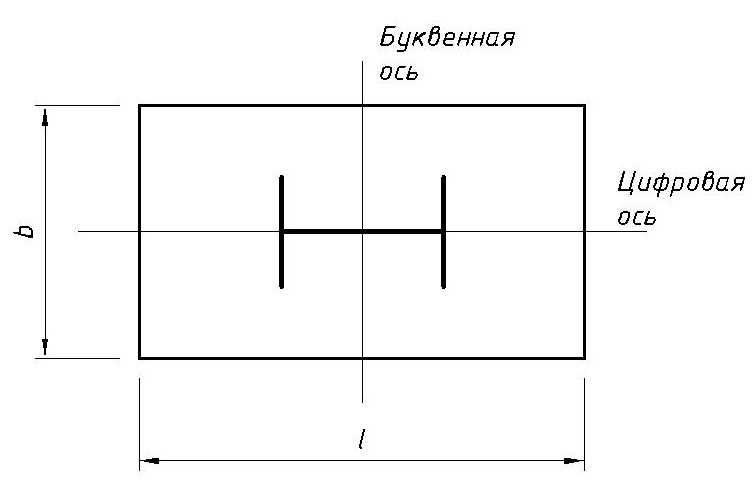
W – момент сопротивления подошвы фундамента, м³. Для прямоугольного сечения находится по формуле W=bl²/6 где в нашем случае b – это сторона подошвы фундамента вдоль буквенной оси, l – длина стороны подошвы фундамента вдоль цифровой оси (см. картинку ниже).

Т.к. предварительно мы приняли фундамент с размерами 1,5х1,5 м, то

W= bl²/6=1.5*1.5²/6=0.5625 м³

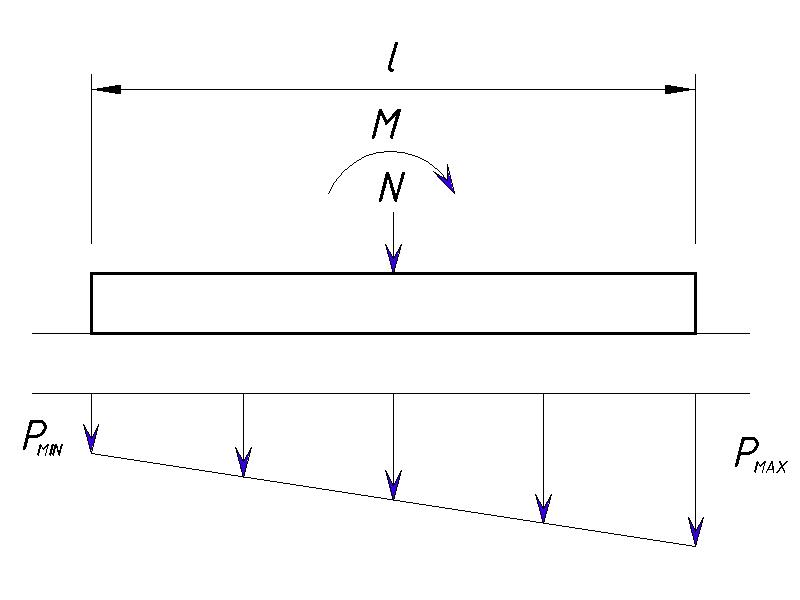
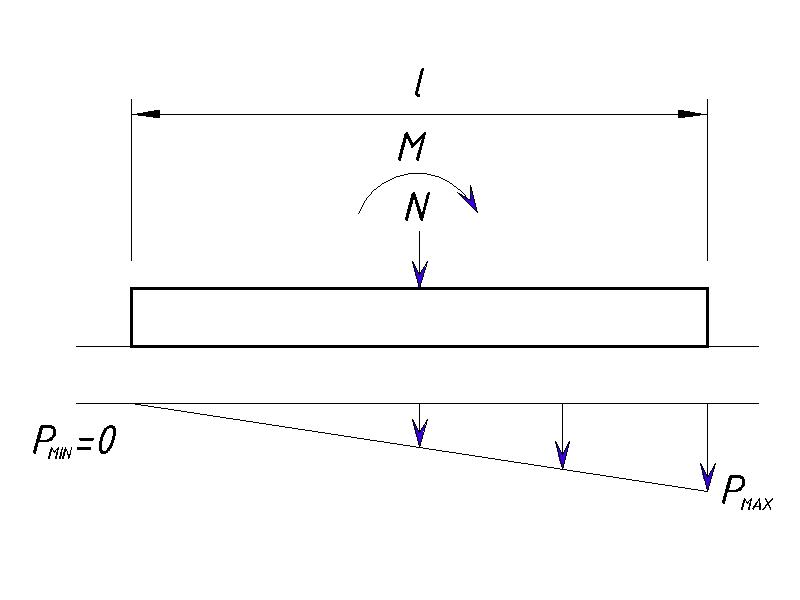
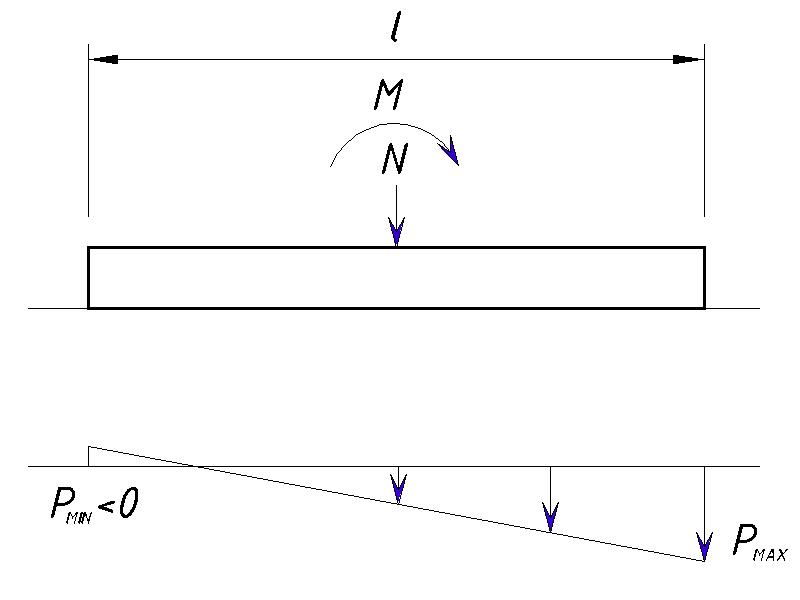
При действии вертикальной нагрузки на фундамент совместно с изгибающим моментом у нас может быть 3 варианта эпюр давления на грунты:

1. Треугольная с отрывом края фундамента

Нельзя допускать, чтобы происходил отрыв фундамента, т.е. Pmin всегда должен быть ≥0.

В нашем случае Pmin 0,5 1,1 1,0 1,0 Примечания

1 К сооружениям с жесткой конструктивной схемой относят сооружения, конструкции которых специально приспособлены к восприятию усилий от деформации оснований, в том числе за счет мероприятий, указанных в 5.9.

2 Для зданий с гибкой конструктивной схемой значение коэффициента γс2 принимают равным единице.

3 При промежуточных значениях L/H коэффициент γс2 определяют интерполяцией.

4 Для рыхлых песков γс1 и γс2 , принимают равными единице.

k=1 (п.5.6.7 СП 22.13330.2016 коэффициент, принимаемый равным единице, если прочностные характеристики грунта (φ_II и С_II ) определены непосредственными испытаниями, и k=1,1, если они приняты по таблицам приложения А).

My=1,68 (таблица 5.5 СП 22.13330.2016)

Mq=7,71 (таблица 5.5 СП 22.13330.2016)

Mc=9,58 (таблица 5.5 СП 22.13330.2016)

Тут хочу обратить внимание, несмотря на то, что мы опираемся на грунт ИГЭ-3, грунт ИГЭ-2 имеет более низкие прочностные характеристики и он заложен ниже грунта ИГЭ-3, поэтому мы принимаем считаем несущую способность основания по ИГЭ-2.

Таблица 5.5 СП 22.13330.2016

Угол внутреннего трения φII, град.	Коэффициенты
My	Mq	Mc
0	0	1,00	3,14
1	0,01	1,06	3,23
2	0,03	1,12	3,32
3	0,04	1,18	3,41
4	0,06	1,25	3,51
5	0,08	1,32	3,61
6	0,10	1,39	3,71
7	0,12	1,47	3,82
8	0,14	1,55	3,93
9	0,16	1,64	4,05
10	0,18	1,73	4,17
11	0,21	1,83	4,29
12	0,23	1,94	4,42
13	0,26	2,05	4,55
14	0,29	2,17	4,69
15	0,32	2,30	4,84
16	0,36	2,43	4,99
17	0,39	2,57	5,15
18	0,43	2,73	5,31
19	0,47	2,89	5,48
20	0,51	3,06	5,66
21	0,56	3,24	5,84
22	0,61	3,44	6,04
23	0,66	3,65	6,24
24	0,72	3,87	6,45
25	0,78	4,11	6,67
26	0,84	4,37	6,90
27	0,91	4,64	7,14
28	0,98	4,93	7,40
29	1,06	5,25	7,67
30	1,15	5,59	7,95
31	1,24	5,95	8,24
32	1,34	6,34	8,55
33	1,44	6,76	8,88
34	1,55	7,22	9,22
35	1,68	7,71	9,58
36	1,81	8,24	9,97
37	1,95	8,81	10,37
38	2,11	9,44	10,80
39	2,28	10,11	11,25
40	2,46	10,85	11,73
41	2,66	11,64	12,24
42	2,88	12,51	12,79
43	3,12	13,46	13,37
44	3,38	14,50	13,98
45	3,66	15,64	14,64

k_z=1 (п.5.6.7 СП 22.13330.2016 коэффициент, принимаемый равным единице при b 150 кПа, поэтому увеличивать размеры фундамента нет необходимости.

Следовательно, фундамент удовлетворяет требованиям по несущей способности основания.

После этого нужно сконструировать фундамент, назначить размеры, арматуру, бетон, что обязательно рассмотрю в следующих статьях.

Расчётную программу в Excel можно скачать по ссылке

This article has 3 Comments

Для всех типов фундаментов для ввода нагрузок на основания применяются результаты статического расчета от действия какого-либо загружения или комбинации загружений. В качестве альтернативы возможен и «ручной» ввод в соответствии с расчетной схемой.

Большое спасибо за программку! Очень сократили время расчетов!

Источник