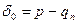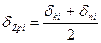Расчет фундаментов по второй группе предельных деформаций

При расчете приняты следующие допущения:

— распределение напряжений в толще основания принимается по теорией однородного изотропного линейно деформуемого полупространства при условии, что зоны пластической деформации грунта под подошвою фундамента могут иметь только ограниченное развитие;

— деформации отдельных слоев неоднородного основания определяются по нормативным давлениям и модулям деформаций, установленным для каждого слоя грунта.

Величина осадки фундамента, равная сжатию всех слоев грунта в пределах активной зоны, определяется по формуле

, (11)

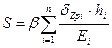
где β= 0,8 – коэффициент, учитывающий стесненность бокового расширения грунта;

h_i – толщина і-го элементарного слоя грунта ниже подошвы фундамента в пределах активной зоны;

Е_i – модуль деформации і-го элементарного слоя грунта в пределах активной зоны;

— середнее значение дополнительного (осадочного) напряжения в пределах і-го слоя грунта от действия нормативных нагрузок.

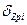
Знак ∑ (суммы) распространяется на все слои грунта в пределах активной зоны ниже подошвы фундамента.

Глубина активной зоны принимается от уровня подошвы фундамента до того уровня, на котором осадочное давление становится равным 0,2 от природного или бытового.

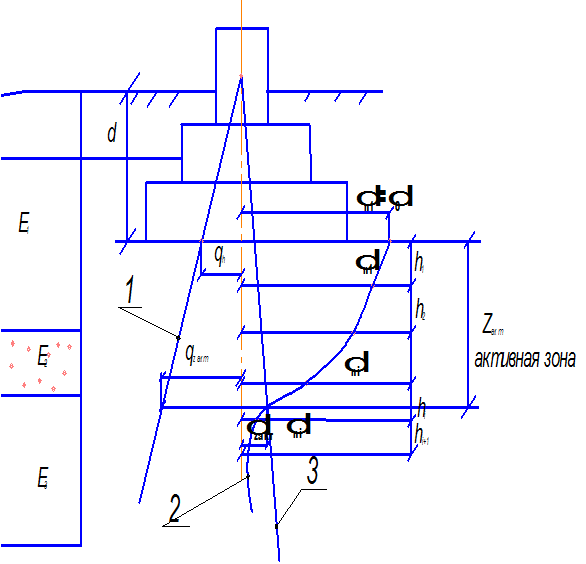
Чтобы воспользоваться формулу (11) выполняют ряд предварительных расчетов и построений (см. рис. 4) :

1. На оси фундамента строится эпюра природных (бытовых) давлений q_h На рассматриваемой глубине оно равно весу вышележащего столба грунта.

2. Толща грунта ниже подошвы фундамента разбивается на n слоев, каждый из которых должен быть однородным по сжимаемости и иметь мощность (∆) не больше 0,4b ( b – меньшая сторона подошвы фундамента), то есть

3. Определяется среднее давление по подошве фундамента от нормативных нагрузок

4. Определяется дополнительное (осадочное) давление в уровне подошвы фундамента

где q_h – природное давление в уровне подошвы фундамента.

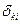
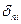
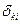
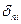
5. Определяются величины , для каждого элементарного слоя

— дополнительное давление на глубине верхней границы элементарного слоя;

— дополнительное давление на глубине нижней границы элементарного слоя.

Знак суммы в формуле распространяется на все слои грунта в пределах активной зоны Z_акт.

Глубина активной зоны z_акт принимается от уровня подошвы фундамента до уровня, на котором дополнительное давление становится равным 0,2 от природного.

1 – эпюра природных (бытовых) давлений; q_h;

2 – эпюра дополнительных давлений;

3 – эпюра 0,2 от природного давления; 0.2q_h.

Рис.4 – Схема к расчету оседания фундамента методом послойного

Источник

Расчет фундамента под наружную стену подвала. Расчет основания по деформациям (по 2 предельному состоянию). Пример расчета.

Наконец, мы переходим к расчету по 2 предельному состоянию, т.е. по деформациям (основное отличие от 1 предельного состояния – в коэффициентах, они равны единице).

Первым делом мы находим расчетное сопротивление грунта основания. Это монотонная и нудная часть расчета с массой коэффициентов, но ее нужно сделать. Можно обратиться к литературе и выбрать приближенное значение расчетного сопротивления грунта, но я рекомендую делать все основательно и четко, поэтому в п. 7.1 мы определим расчетное сопротивление по формуле, как полагается.

Далее нам снова нужно найти горизонтальное давление на отметке поверхности земли σ₁ и на отметке низа подошвы σ₂. По сути, необходимо повторить действия пунктов 5.1…5.10, только с другими значениями характеристик грунтов (для второго предельного состояния) и без повышающих коэффициентов.

Затем, как и в прошлый раз нам нужно выбрать один из двух вариантов. В нашем случае это снова вариант «а» — когда σ₁ меньше нуля, и эпюра треугольная.

Итоговая эпюра снова окажет нам помощь в самопроверке:

А для варианта «б» расчет будет выглядеть вот так (хоть сейчас он нам и не нужен, но вдруг кому-то пригодится):

Значения σ₃ и σ₄ введены для удобства расчета усилий Мн и Qн в пунктах 7.18 и 7.19.

Далее мы находим все вертикальные силы с нормативным значением (без повышающих коэффициентов)

И по формулам из таблицы 5 руководства определяем Мн и Qн. После чего можно найти сумму моментов относительно оси, проходящей через центр тяжести подошвы.

Когда нам известны итоговые вертикальная сила и момент, мы можем найти эксцентриситет приложения действующей нагрузки. И здесь расчет опять расходится на два варианта. Как показано на рисунке ниже, эксцентриситет может быть небольшим, и тогда в расчете по деформациям будет задействована вся ширина подошвы, а эпюра напряжений под подошвой будет в виде трапеции; а может быть так, что место приложения нагрузки сильно смещено от центра тяжести подошвы – тогда подошва будет отрываться от основания, и эпюра напряжений будет треугольной и только под частью подошвы. В нашем случае эксцентриситет крайне мал, и эпюра напряжений будет близка к прямоугольнику. Проверив условие, мы убедимся, что считать нужно по варианту «а», по нему мы и определим напряжения под подошвой фундамента.

Вариант «б» в данном примере в расчете не участвует.

В пункте 7.22 мы проверяем условие – сравниваем среднее давление под подошвой с расчетным сопротивлением грунта. Если условие удовлетворяется, переходим к следующей стадии расчета. Если же нет, то скорее всего нам придется увеличить ширину подошвы ленточного фундамента – это самый простой путь. Также возможны специальные мероприятия в виде усиления грунта под подошвой или устройства искусственной подушки.

По сути, на этом расчет, определяющий габариты фундамента и стены подвала окончен. Проверены все необходимые условия (отмечены синим на рисунках), все проходит, все получилось.

Источник

Первое и второе предельное состояние при расчете конструкций

Что такое предельные состояния и как с ними разобраться применительно к расчетам конструкций? Все знают, что бывает две группы предельных состояний: первая и вторая. Что же обозначает это разделение?

Само название «предельное состояние» обозначает, что для любой конструкции при определенных условиях наступает такое состояние, при котором исчерпывается какой-то определенный предел. Условно, для удобства расчетов, таких пределов вывели два: первое предельное состояние – это когда исчерпывается предел прочности, устойчивости и выносливости конструкции; второе предельное состояние – когда деформации конструкции превышают предельно допустимые (ко второму предельному состоянию для железобетона также относят ограничение по возникновению и раскрытию трещин).

Перед тем, как перейти к разбору расчетов по первому и второму предельному состоянию, следует разобраться, какая часть расчета конструкции вообще делится на эти две части. Любой расчет начинается со сбора нагрузки. Затем следует выбор расчетной схемы и непосредственно расчет, в результате которого мы определяем усилия в конструкции: моменты, продольные и поперечные силы. И только после того, как усилия определены, мы переходим к расчетам по первому и второму предельному состоянию. Обычно они выполняются именно в такой последовательности: сначала по первому, потом по второму. Хотя бывают и исключения, но о них ниже.

Нельзя сказать, что для какой-то конструкции важнее: прочность или деформативность, устойчивость или трещиностойкость. Нужно проводить расчет по двум предельным состояниям и выяснять, какое из ограничений бывает наиболее неблагоприятным. Но для каждого типа конструкций есть свои особые моменты, которые полезно знать, чтобы было проще ориентироваться в среде предельных состояний. В этой статье мы на примерах разберем предельные состояния для различных типов железобетонных конструкций.

Расчет балок, плит и других изгибаемых элементов по первому и второму предельному состоянию

Итак, вам нужно рассчитать изгибаемый элемент, и вы думаете, с чего начать расчет, и как понять, все ли посчитано? Все рекомендуют сделать расчет не только по первому, но и по второму предельному состоянию. Но что же это такое? Где конкретика?

Для расчета изгибаемых элементов вам понадобится «Пособие по проектированию бетонных и железобетонных конструкций из тяжелых бетонов без предварительного напряжения арматуры (к СНиП 2.03.01-84)» и непосредственно сам СНиП 2.03.01-84 «Бетонные и железобетонные конструкции» обязательно с изменением 1 (очень важным для расчета по второй группе предельных состояний).

Открываете раздел 3 пособия «Расчет железобетонных элементов по предельным состояниям первой группы», а именно «Расчет железобетонных элементов по прочности» (начиная с п. 3.10). Теперь нужно выяснить, из каких этапов он состоит:

1) Расчет сечений, нормальных к продольной оси элемента – это та часть расчета, в которой мы проверяем, выдержит ли наша конструкция воздействие изгибающего момента. Проверяется сочетание двух важных факторов: размер сечения элемента и площадь продольной арматуры. Если проверка показывает, что действующий на конструкцию момент меньше предельно допустимого, значит все хорошо, и можно переходить к следующему этапу.

2) Расчет сечений, наклонных к продольной оси элемента – это расчет конструкции на действие поперечной силы. Для проверки нам важно установить размеры сечения элемента и площадь поперечной арматуры. Так же, как и на предыдущем этапе расчета, если действующая поперечная сила меньше предельно допустимой, прочность элемента считается обеспеченной.

Оба этапа вместе с примерами подробно рассмотрены в пособии. Эти два расчета являются исчерпывающими расчетами по прочности для классических изгибаемых элементов. Если есть какие-либо особые условия (многократно повторяющиеся нагрузки, динамика), их нужно учитывать в расчете на прочность и выносливость (зачастую, учет производится введением коэффициентов).

Далее открываем раздел 4 пособия «Расчет бетонных и железобетонных элементов по предельным состояниям второй группы». Рассмотрим этапы, из которых он состоит.

1) Расчет железобетонных элементов по образованию трещин – это самый первый этап, в котором мы выясняем, образуются ли трещины в нашем элементе при воздействии действующих на него усилий. Трещины не образуются, если наш максимальный момент Mr меньше момента Mcrc, вызывающего образование трещин.

2) Расчет железобетонных элементов по раскрытию трещин – это следующий этап, на котором мы проверяем величину раскрытия трещин в конструкции и сравниваем ее с допустимыми размерами. Обратите внимание на п. 4.5 пособия, в котором оговаривается, в каких случаях этот расчет выполнять не нужно – лишняя работа нам ни к чему. Если же расчет необходим, то нужно выполнить две его части:

а) расчет по раскрытию трещин, нормальных к продольной оси элемента – его мы выполняем по п. 4.7-4.9 пособия ( с обязательным учетом изменения 1 к СНиП , т.к. расчет там уже кардинально другой);

б) расчет по раскрытию трещин, наклонных к продольной оси элемента – его нужно выполнять по п. 4.11 пособия, также с учетом изменения 1.

Естественно, если согласно первому этапу расчета трещины не образуются, то этап 2 мы пропускаем.

3) Определение прогиба – это последний этап расчета по второму предельному состоянию для изгибаемых железобетонных элементов, выполняется он согласно п. 4.22-4.24 пособия. В этом расчете нам нужно найти прогиб нашего элемента и сравнить его с прогибом, нормированным ДСТУ Б. В.1.2-3:2006 «Прогибы и перемещения».

Если все эти части расчетов выполнены, считайте, что расчет элемента как по первому, так и по второму предельному состоянию выполнен. Конечно, если есть какие-то особенности конструкции (подрезка на опоре, отверстия, сосредоточенные нагрузки и т.д.), то нужно дополнять расчет с учетом всех этих нюансов.

Расчет колонн и других центрально и внецентренно сжатых элементов по первому и второму предельному состоянию

Этапы этого расчета не особо отличаются от этапов расчета изгибаемых элементов, да и литература та же.

Расчет по предельному состоянию первой группы включает в себя:

1) Расчет сечений, нормальных к продольной оси элемента – этот расчет так же, как и для изгибаемых элементов, определяет необходимый размер сечения элемента и его продольное армирование. Но в отличие от расчета изгибаемых элементов, где проверяется прочность сечения на действие изгибающего момента М, в данном расчете выделяется максимальная вертикальная сила N и эксцентриситет приложения этой силы «е» (при перемножении, правда, они дают все тот же изгибающий момент). В пособии подробно изложена методика расчета для всех стандартных и нестандартных сечений (начиная с п. 3.50).

Особенностью данного расчета является то, что нужно учитывать влияние прогиба элемента, а также учитывается влияние косвенного армирования. Прогиб элемента определяется при расчете по второй группе предельных состояний, но допускается при расчете по первому предельному состоянию упростить расчет путем введения коэффициента согласно п. 3.54 пособия.

2) Расчет сечений, наклонных к продольной оси элемента – этот расчет на действие поперечной силы согласно п. 3.53 пособия аналогичен расчету изгибаемых элементов. В результате расчета мы получаем площадь поперечной арматуры в конструкции.

Расчет по предельному состоянию второй группы состоит из этапов:

1) Расчет железобетонных элементов по образованию трещин.

2) Расчет железобетонных элементов по раскрытию трещин.

Эти два этапа абсолютно аналогичны расчету изгибаемых элементов – имеются максимальные усилия, следует определить, образуются ли трещины; и если образуются, то сделать при необходимости расчет по раскрытию трещин, нормальных и наклонных к продольной оси элемента.

3) Определение прогиба. Точно так же, как и для изгибаемых элементов, нужно определять прогиб и для внецентренно сжатых элементов. Предельные прогибы как всегда можно найти в ДСТУ Б В.1.2-3:2006 «Прогибы и перемещения».

Расчет фундаментов по первому и второму предельному состоянию

Расчет фундаментов кардинально отличается от приведенных выше расчетов. Как всегда, при расчете фундаментов необходимо начать со сбора нагрузок либо с расчета каркаса здания, в результате которого определяться основные нагрузки на фундамент N, M, Q.

После того, как собраны нагрузки и выбран тип фундамента, необходимо перейти к расчету грунтового основания под фундаментом. Этот расчет, как и любые другие расчеты, делится на расчет по первому и по второму предельному состоянию:

1) обеспечение несущей способности основания фундамента – проверяется прочность и устойчивость оснований (первое предельное состояние) – пример расчета ленточного фундамента здесь;

2) расчет основания по деформациям – определение расчетного сопротивления грунта основания, определение осадки, определение крена фундамента (второе предельное состояние).

Разобраться с этим расчетом поможет «Пособие по проектированию оснований зданий и сооружений (к СНиП 2.02.01-83)».

Как вы уже поняли из формулировок, при определении размера подошвы фундамента (будь то лента или столбчатый фундамент), мы прежде всего выполняем расчет грунтового основания, а не фундамента. И в этом расчете (кроме скальных грунтов) намного важнее выполнить расчет основания по деформациям – все, что перечислено в пункте 2 выше. Расчет по первому предельному состоянию зачастую выполнять вообще не требуется, т.к. предотвратить деформации гораздо важнее, они возникают намного раньше, чем потеря грунтом несущей способности. В каких случаях следует выполнять расчет по первой группе предельных состояний, можно узнать из п. 2.259 пособия.

Теперь рассмотрим расчет основания по деформациям. Чаще всего проектировщики прикидывают расчетное сопротивление грунта, сравнивают его с нагрузкой на грунт от здания, подбирая необходимую площадь фундамента, и на этом останавливаются. Это неверный подход, т.к. выполнена лишь часть работы. Расчет фундамента считается завершенным, когда выполнены все этапы, перечисленные в пункте 2.

Очень важным является определение осадки фундаментов. Особенно это важно при различных нагрузках или неравномерных грунтах, когда есть риск возникновения неравномерных осадок фундаментов (подробно об этом изложено в этой статье «Что нужно знать о ленточном монолитном фундаменте»). Чтобы быть уверенным в дальнейшей целостности конструкций здания, всегда нужно проверять разность осадок фундаментов по таблице 72 пособия. Если разность осадок выше предельно допустимой, возникает риск возникновения трещин в конструкциях.

Крен фундамента необходимо определять при наличии изгибающих моментов, действующих на фундамент. Также крен нужно проверять при неравномерной нагрузке на грунте – она также влияет на деформации грунтового основания.

Но после того, как выполнен расчет основания по второму и возможно первому предельному состоянию и определены размеры подошвы фундамента, нужно перейти к следующему этапу: расчету самого фундамента.

При расчете основания мы определили давление под подошвой фундамента. Это давление прикладывается к подошве как нагрузка (направленная снизу вверх), а опорой служит колонна или стена, опирающаяся на фундамент (такой себе перевертыш). Получается, что в каждую сторону от опоры мы имеем консоль (обычно эти консоли одинаковые), и их нужно рассчитать с учетом равномерно распределенной нагрузки, равной давлению под подошвой фундамента. Хорошо понять принцип расчета на примере столбчатого фундамента можно с помощью «Пособия по проектированию фундаментов на естественном основании под колонны зданий и сооружений (к СНиП 2.03.01-84 и СНиП 2.02.01-83)» — там в примерах изложены все этапы расчета, как по первому, так и по второму предельному состоянию. По результатам расчета консоли мы сначала определяем высоту ее сечения и армирование (это расчет по первому предельному состоянию), затем проверяем трещиностойкость (это расчет по второму предельному состоянию).

Точно так же нужно действовать и в случае расчета ленточного фундамента: имея вылет подошвы в одну сторону от стены и давление под этой подошвой, мы рассчитываем консольную плиту (с защемлением на опоре), длина консоли равна вылету подошвы, ширина берется для удобства расчета равной одному метру, нагрузка на консоль равна давлению под подошвой фундамента. Находим максимальный момент и поперечную силу в консоли и выполняем расчет по первому и второму предельному состоянию – точно так, как описано в расчете изгибаемых элементов.

Таким образом, при расчете фундаментов мы проходим два случая расчета по предельным состояниям первой и второй группы: сначала при расчете основания, затем при расчете непосредственно фундамента.

Выводы. При любом расчете важно соблюсти последовательность:

1) Сбор нагрузок.

2) Выбор расчетной схемы.

3) Определение усилий N, M и Q.

4) Расчет элемента по первому предельному состоянию (по прочности и устойчивости).

5) Расчет элемента по второму предельному состоянию (по деформативности и трещиностойкости).

Источник