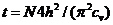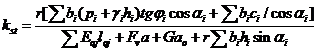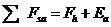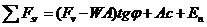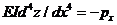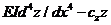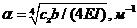Расчет гибких фундаментов с помощью метода местных деформаций

Строй-справка.ру

Отопление, водоснабжение, канализация

Для получения полного решения уравнения (7.6) необходимо к общему решению (7.7) добавить частное решение z, зависящее от нагрузки q0. При условии, если q0 может быть представлена алгебраическим полиномом степени не выше третьей от х, то частное решение может быть найдено с помощью полинома соответствующей степени с помощью метода неопределенных коэффициентов.

Постоянные интегрирования выражения (7.7) определяют из граничных условий.

В общем случае действия на балку различных нагрузок, разбивая балку на определенное количество участков, приходится для каждого из них находить свои значения произвольных постоянных. Это приводит к необходимости для различных, встречающихся на практике, нагрузок составлять и решать большое количество уравнений со многими неизвестными, что существенно усложняет расчет. Однако дальнейшие исследования показали, что в большинстве случаев любую систему нагрузок, приложенных к балке конечной длины, удается заменить системой балок бесконечной длины, прикладывая в их сечениях фиктивные силы и моменты, обеспечивая при этом выполнение граничных условий и заменяя на основании принципа независимости действия сил решение сложной задачи системой простых схем, расчетные усилия для которых известны.

Учет сдвигающих напряжений, вовлекающих в работу ненагруженные зоны грунта рядом с нагруженными, с помощью второго коэффициента постели позволил значительно усовершенствовать метод местных упругих деформаций.

Главное отличие данной модели заключается в том, что основание с двумя коэффициентами постели имеет осадки и за пределами лежащей на нем балки.

Расчет плит с помощью метода местных деформаций значительно сложнее расчета балок.

В настоящее время разработано достаточно большое количество методов расчета, позволяющих получать решение уравнения (7.13) с помощью использования алгебраических полиномов, компенсирующих нагрузок, вариационных методов, конечных элементов и конечных разностей. Разработан целый комплекс программ, дающих возможность проводить расчет плитных фундаментов на ЭВМ с дополнительным учетом касательных напряжений по подошве фундамента, а также жесткости надфундаментных конструкций.

Согласно теории местных упругих деформаций при равномерной нагрузке на балку реакция основания будет одинаковой по всей площади контакта с грунтом, что не подтверждается экспериментальными данными. Аналогичный результат будет получен и при расчете по данному методу жестких фундаментных конструкций.

Еще раз заметим, что метод местных упругих деформаций допускается применять при проектировании гибких фундаментов при наличии в основании слабых грунтов или слоя сжимаемого грунта небольшой мощности.

Рис. 7.2. Схема длинной балки, затру- подстилаемого плотным несжиженнои посередвдеойСосредото,енной маемым.

Источник

Гибкие фундаменты. Методы их расчета

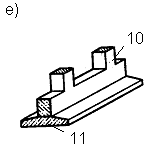
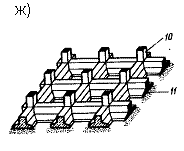
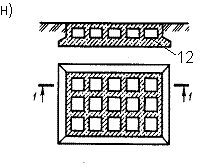
К гибким фундаментам относятся все ленточные железобетонные фундаменты, фундаменты из монолитного железобетона под отдельные опоры или группы опор (рис. 7 е), фундаменты из перекрестных лент (рис. 7 ж), коробчатые плиты (если необходимо воспринять очень большие изгибающие моменты, возникающие в сплошных плитах, например у фундаментов высотных зданий) (рис. 7 н), круглые (рис. 7 г) или кольцевые (рис. 7 п) в плане плиты, сплошные железобетонные плиты под колонны(рис. 7 р).

На усилия в конструкции гибкого фундамента влияет его жесткость, жесткость основания и жесткость надземных конструкций.

В зависимости от протяженности гибких фундаментов различают плоскую задачу, когда фундамент в каждом сечении по его длине имеет одинаковую форму деформации и пространственную задачу в двух случаях: 1. балка на упругом основании. 2. фундаментная плита на упругом основании.

Теория местных деформаций: реакция грунта основания в каждой точке подошвы фундамента (балки) прямо пропорциональна осадке этой точки, т.е. p_y=C_zZ

C_z – коэффициент постели (упругого сжатия основания); Z – осадка в месте определения реакции грунта p_y.

Теория упругого пространства является другой крайней теорией расчета балок и плит на упругом основании. В этом случае фундаментная балка принимается лежащей на однородном упругом или линейно деформируемом бесконечном полупространстве.

Теория расчета балок на упругом (линейно деформируемом) слое грунта конечной толщины. Основной сложностью использования этой теории является установление толщины деформируемого слоя. Это можно сделать, руководствуясь способом определения расчетной мощности сжимаемой толщи при расчете осадки фундаментов методом ограниченной фундаментной толщи.

При предварительном подборе сечения балки на упругом основании обычно принимают равномерное или трапециевидное распределение давления по подошве.

Источник

Расчет гибких ф. с помощью метода местных деформаций

Теории расчета балок и плит на упругом основании и условия их применимости к расчету гибких фундаментов

Для гибких ф., которые в основном воспринимают изгибающие моменты, образующиеся в результате совместной работы с основанием, предположение о линейном распределении реактивных давлений оказывается неприемлемым, потому что оно зависит от жесткости ф. и податливости грунтового основания.

Замена реальной эпюры контактных давлений линейно распределенной приводит к существенным погрешностям при определении изгибающих моментов и перечных сил.

К гибким ф. можно отнести ленточные и отдельные ж. б. ф., а также сплошные ж. б. плиты и некоторые типы коробчатых ф.

В настоящее время большое распространение при проектировании гибких ф. получили теории расчета балок и плит на упругом основании, которые справедливы для линейно деформируемых оснований, причем наибольшее применение получили следующие методы:

— местных деформаций с постоянным и переменными коэффициентами постели;

— упругого слоя ограниченной толщины на несжимаемом основании;

— упругого слоя с переменным модулем деформации основания по глубине.

Эти теории исходят из предположения о совместности деформации, ф. и грунта, т.е. считается, что перемещение ф. в данной точке контакта равно осадке поверхности грунта.

В основу расчета гибких ф. по этому методу положена гипотеза о том, что осадка в данной точке основания не зависит от осадки других точек и прямо пропорциональна реактивному давлению в этой точке, что выражается зависимостью

где z – осадка основания в точке действия реактивного давления p(x); k_S – коэфф. пропорциональности («коэфф. постели»), Па/м, зависящий от физических свойств грунтов.

Подставляя эту зависимость в дифференциальное уравнение изгиба балки, получим дифференциальное уравнение изгиба балки на упругом основании по методу местных упругих деформаций

EJz IV +bk_Sz=q(x),

где q(x) – внешняя нагрузка на ф.;

EJ – изгибная жесткость ф.;

b – ширина ф.

Для получения полного решения данного дифф. уравнения необходимо к общему решению (при q(x)=0) добавить частное решение, зависящее от q(x).

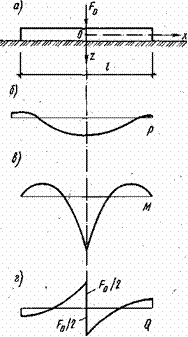
В частности, рассматривая случай загружения бесконечно длинного гибкого ф. сосредоточенной силой, приложенной в середине, получим следующие выражения

z(x)=P/(8EJa 3 )e — a x (cosax+sinax);

M(x)=P/(4a)e — a x (cosax-sinax);

Q(x)=-P/2e — a x cosax,

где a=(k_Sb/(4EJ)) 1/4 – упругая характеристика ф.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Лекция 21. Проектирование гибких фундаментов

Проектирование гибких фундаментов

При расчете жестких фундаментов была принята линейная зависимость распределений напряжений под подошвой фундамента. При расчете фундаментов конечной жесткости (гибких фундаментов — балок и плит) условная линейная эпюра распределения напряжений под подошвой гибкого фундамента не приемлема.

В этом случае необходимо учитывать M и Q, возникающие в самой конструкции фундамента, вследствие действия неравномерных контактных реактивных напряжений по подошве фундамента. Не учет возникающих усилий может привести к неправильному выбору сечения фундамента или % его армирования.

Поэтому необходимо решать задачу совместной работы фундаментной конструкции и сжимаемого основания.

Какие же фундаменты считать гибкими?

Гибкие фундаменты — это те, деформации изгиба которых того же порядка, что и осадки этого же фундамента

∆ S(см) ≈ f(см); ∆ S – осадка фундамента (деформация основания)

f – деформация изгиба фундамента

Таким образом, при расчете гибких фундаментов необходимо одновременно учитывать и деформации фундамента и его осадки.

конструкция грунт

При расчете ленточных фундаментов, загруженных неравномерно сосредоточенными силами — необходимо учитывать изгиб в продольном направлении.

Вследствие изгиба фундамента конечной жесткости давление на грунт увеличивается в местах передачи фундаменту сосредоточенных сил и уменьшается в промежутках между этими силами.

Единого метода расчета гибких фундаментов нет, а существует несколько способов.

Критерий, определяющий состояние фундамента

h > — абсолютно жесткие фундаменты

h 10 — жёсткая балка (метод Горбунова-Посадова)

Г>10 — гибкая балка

Часто при расчете гибких фундаментов (особенно если жесткость балки применима)- переходят к решению задач по методу (Исследование приемов строительной механики для решения статически неопределимых систем).

Метод Жемочника для расчета фундаментных балок

на упругом основании.

В основу метода положены следующие допущения:

1. Действительная криволинейная эпюра

распределения давлений под подошвой

балки заменяется ступенчатой

Распределение давлений на ширине балки

также принимаются равномерным.

2. Между балкой и сжимаемым основанием предполагаются жесткие шарниры опирающиеся стержни, воспринимающие усилия от балки и равномерно распределяющие это усилие на основание.

4. Условие совместимости работы балки и основания и удовлетворяются равенством прогиба балки и осадки основания в месте закрепления опорного стержня yi=Si.

Этот метод является универсальным и позволяет решать любые задачи с любой степенью сложности.

Задача решается смешанным методом.

— единичное перемещение по направлению «к» связи от воздействия «i» связи

— единичное перемещение, вызванное осадкой основания

— единичное перемещение, вызванное прогибом балки

; — находятся обычно по таблицам

Решив систему уравнений и найдя Xi, определяют величины реактивных давлений Рi, соответствующих ширине принятых участков ступенчатой эпюры (см. допущение № 1):

Затем с использованием метода сечений строят эпюры изгибающих моментов M, а по ним окончательно определяют сечение балки и ее армирование

Источник

Расчет гибких фундаментов с помощью метода местных деформаций

41. Определение осадки фундаментов путем непосредственного применения теории линейно деформируемой среды (полупространства).

42. Расчет осадки фундаментов мелкого заложения во времени (определение времени затухания осадки). Основные положения.

Если в основании залегают водонасыщенные глинистые грунты, осадка может развиваться в течение длительного периода времени.

В подавляющем большинстве случаев временной процесс развития осадок связан с очень малой скоростью фильтрации воды в глинистых грунтах (кэф фильтрации порядка 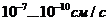) и обусловленным этим медленным уплотнением водонасыщенных грунтов. Однако в глинистых грунтах тугопластичной и твёрдой консистенции при высоком содержании глинистых частиц к этому могут добавляться ещё и крайне медленно протекающие процессы ползучести грунтов.

При степени водонасыщения 0.8-1 в поровой воде содержится некоторое количество пузырьков воздуха, что существенно усложняет процесс формирования и изменения напряженно-деформированного состояния массивов глинистых грунтов во времени.

Современные методы прогнозы развития деформаций грунтов во времени основаны на теории фильтрационной консолидации, разработанной в 1924 г. К.Терцаги и получившей дальнейшее развитие.

В основу теории Терцаги-Гереванова, разработанной для одномерной задачи консолидации однородного слоя грунта, положены следующие препосылки:

— скелет грунта рассматривается как упругая пористая среда и любое приращение напряжений в скелете грунта мгновенно вызывает соответствующее приращение деформаций;

— поровая вода принимается абсолютно несжимаемой;

— отжатие воды из пор в процессе уплотнения грунта подчиняется закону ламинарной фильтрации Дарси;

— в процессе уплотнения грунта в любой момент времени внешняя нагрузка уравновешивается суммой напряжений в скелете грунта.

Время, соответствующее заданной степени консолидации – степени уплотнения грунта – слоя грунта:

43. Определение крена фундаментов.

Крен фундамента может быть вызван внецентренным приложением равнодействующей внешних сил, влиянием соседних фундаментов или неоднородностью грунтов основания.

В случае внец. приложения нагрузки крен жёсткого фундамента определяется по формуле 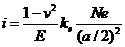, где Е и v – соответственно модуль деформации и кэф Пуассона грунта основания; Ке – табличный кэф; N – вертикальная составляющая равнодействующей всех нагрузок на фундамент в уровне его подошвы; е – эксцентриситет приложения равнодействующей; а – диаметр круглого или сторона прямоугольного фундамента, в направлении которой действует момент.

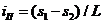
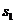
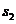
Если причиной возникновения крена является нагружение соседнего фундамента или действие какой-либо другой односторонней нагрузки, то его определяют по формуле: , где и — осадки противоположных сторон фундамента; L – расстояние между рассматриваемыми точками.

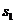
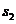
По этой же формуле определяют крен, вызванный неоднородностью грунтов основания, а также крен жёсткого сооружения, опирающегося на систему фундаментов. В последнем случае и — соответственно большая и меньшая осадки фундаментов системы; а L – расстояние между осями этих фундаментов.

Крен не определяется, если конструкция надземной части сооружения исключает их поворот.

44. Аналитический метод расчета на глубокий сдвиг фундаментов с горизонтальной подошвой при действии внецентренной наклонной нагрузки.

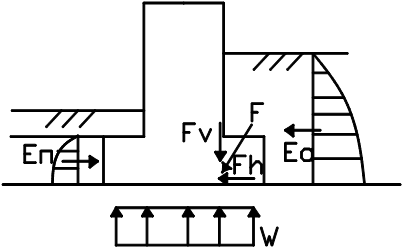
При большой глубине подвала стены испытывают значительное давление грунта засыпки с внешней стороны здания. Потеря устойчивости может иметь форму поворота фундамента вокруг некоторого центра вращения. В этом случае проводятся расчёты устойчивости фундамента в предположении кругло-цилиндрической поверхности скольжения.

Исходя из кинематических условий в качеств центра вращения точка, лежащая на краю верхнего обреза фундамента. Принимается, что след поверхности скольжения в плоскости поперечного сечения фундамента соответствует части окружности радиусом р, выходящей из точки, лежащей на противоположном краю подошвы фундамента, и заканчивающейся в точке пересечения её с основанием. Фундамент и прилегающий к нему грунт выше поверхности скольжения называется отсеком обрушения. 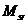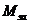Кэф устойчивости в этом случае определяется как отношение момента сил, удерживающих отсек обрушения , к моменту сил , стремящихся повернуть этот отсек относительно точки О.

Если, аналогично предыдущему, определить удерживающие и опрокидывающие силы, то формула примет вид:

bi и hi – ширина и высота i — o го элемента; гамма i – средний удельный вес грунтов в i -ом элементе; фи i и с i – угол внутреннего трения и сцепление грунта по подошве итого элемента;

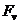
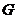
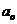
р итое – среднее давление, передаваемое фундаментом на итый элемент; альфа итое – угол между вертикалью и нормалью к подошве итого элемента; Еа джитое и l а джитое – равнодействующая и плечо сил активного давления; и а – равнодействующая и плечо силы, которой нагружен фундамент; и — вес фундамента и соответствующее плечо; r – радиус поверхности скольжения.

45. Аналитический метод расчета несущей способности двухслойного основания.

46. Расчёт устойчивости фундамента по схеме плоского сдвига.

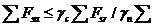
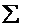
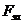
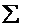
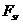
В этом случае: — соответственно суммы проекций на плоскость скольжения расчётных сдвигающих и удерживающих сил.

Эти величины можно выразить формулами:

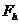
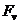
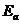
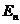
где и — касательная и нормальная составляющие равнодействующей F в уровне подошвы фундамента; W – взвешивающее давление воды на подошву фундамента при высоком залегании уровня подземных вод; А – площадь подошвы фундамента; и — равнодействующие активного и пассивного давления грунта на фундамент.

47. Расчет ленточных фундаментов на изгиб .

В задачу расчёта гибкого ленточного фундамента входят определение реактивного давления грунта по подошве фундамента, вычисление внутренних усилий, действующих в фундаменте, установление размеров поперечного сечения фундамента и его необходимого армирования.

При расчёте реактивного давления грунта гибкий ленточный фундамент рассматривается как балка на упругом основании, изгибающаяся под действием приложенных к ней внешних нагрузок. Если пренебречь трением между подошвой фундаментной балки и грунтов основания, что идёт в запас прочности, дифференциальное уравнение её изгиба можно представить в виде:

где EI – жёсткость балки; z – прогиб балки в точке с координатой х; рх – реактивное давление в той же точке.

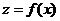
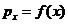
В этом диф.уре. имеются две неизвестные функции: уравнение изогнутой оси балки и закон распределения реактивных давлений грунта , поэтому решение может быть получено лишь при условии составления второго уравнения, в котором будут связаны между собой осадки различных точек балки и реактивное давление грунта.

В зависимости от гипотезы, принятой для установления второго уравнения, различают два основных метода расчёта балки, лежащей на упругом основании: метод местных деформаций и метод упругого полупространства.

Диф.ур. содержит жёсткость фундамента EI , что требует предварительного назначения размеров его сечения. Это делают исходя из схемы линейного распределения реактивных усилий, принимая равномерное или трапециевидное распределение давления по подошве.

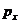
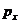
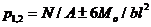
Допустим имеется фундаментная балка, загруженная системой сил, в результате чего действует реактивное давление грунта , изменяющееся по какому-то сложному закону. Заменяя криволинейную эпюру распределения реактивных давлений линейной трапециевидной, определяем краевые значения давления .

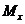
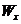
Определив краевые значения прямолинейной эпюры давлений, загружаем ею рассматриваемую фундаментную балку, как внешней нагрузкой. Далее определяем , и по максимальному значению момента из условия обеспечения необходимой прочности находим , а уже по нему подбираем предварительные размеры фундаментной балки и устанавливаем её жёсткость EI .

48. Расчет столбчатых фундаментов на изгиб и продавливание .

49. Теории изгиба балок и плит на упругом основании и условия их применимости к расчету гибких фундаментов .

Для гибких фундаментов, которые в основном воспринимают изгибающие моменты, образующиеся в результате совместной работы с основанием, предположение о линейном распределении реактивных давлений оказывается неприемлемым, потому что оно зависит от жесткости фундамента и податливости грунтового основания.

Замена реальной эпюры контактных давлений линейно распределенной приводит к существенным погрешностям при определении изгибающих моментов и поперечных сил.

К гибким фундаментам можно отнести ленточные и отдельные железобетонные фундаменты, а также сплошные железобетонные плиты и некоторые типы коробчатых фундаментов.

В зависимости от вида используемого фундамента различают плоскую задачу, когда условия работы поперечного сечения фундамента одинаковы по длине. Например, ленточный фундамент под стену в поперечном сечении имеет одинаковую форму деформации по всей длине.

В условиях пространственной задачи будет находиться ленточный фундамент под колонны, принимаемый в поперечном направлении жестким, и фундаментные плиты различной формы, работающие на изгиб в двух направлениях.

В настоящее время большое распространение при проектировании гибких фундаментов получили теории расчета балок и плит на упругом основании, которые справедливы для линейно деформируемых оснований, причем наибольшее применение получили следующие методы:

1) местных деформаций с постоянным и переменными коэффициентами постели;

2) упругого полупространства;

3) упругого слоя ограниченной толщины на несжимаемом основании;

4) упругого слоя с переменным модулем деформации основания по глубине.

Эти теории исходят из предположения о совместности деформации, фундамента и грунта, т. е. считается, что перемещение фундамента в данной точке контакта равно осадке поверхности грунта.

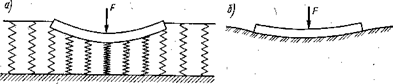
В методе местных упругих деформаций не учитываются осадки грунта основания за пределами площади загружения, что дает возможность представить такое основание в виде системы несвязанных между собой упругих пружин (рис. 7.1, а). Такие условия работы грунтового основания не подтверждаются экспериментальными данными, которые показывают, что в реальных условиях нагружения оседают не только нагруженная поверхность, но и соседние участки грунта (рис. 7.1, б). Это ограничивает область применения данного метода на практике.

Рис. 7.1. Схемы упругого основания

Метод местных упругих деформаций используют для слабых грунтов основания, для которых можно не учитывать осадки вне зоны приложения внешней нагрузки или в случае незначительной мощности деформируемого грунта, подстилаемого скальным основанием при полупролете рассчитываемого фундамента.

С целью расширения области применения данного метода для расчета гибких фундаментов стали учитывать переменное значение коэффициента постели по длине балки в зависимости от уровня действующего реактивного давления.

Метод упругого полупространства не имеет недостатков, присущих методу местных деформаций, так как он базируется на решениях классической теории упругости, рассматривающей однородные, упругие линейно деформируемые тела.

В соответствии с этими решениями осадки основания имеют место не только на участке под гибким фундаментом, но и за его пределами (рис. 7.1, б).

Однако и метод расчета гибких фундаментов при моделировании грунтового основания упругим полупространством не свободен от некоторых недостатков. В частности, экспериментальными исследованиями было доказано, что осадки за пределами площади загружения затухают значительно быстрее, чем это происходит согласно решению задачи деформирования упругого полупространства. Это связано с тем, что исходные предпосылки теории упругости могут быть применимы к грунтам только с некоторыми ограничениями, допускающими некоторую идеализацию реальных свойств.

Наблюдения за деформациями оснований гибких фундаментов показали, что основные деформации уплотнения грунта происходят в пределах относительно небольшой глубины. Анализ результатов таких наблюдений показал, что поверхность грунта под возводимыми зданиями и гибкими фундаментами деформируется в соответствии с расчетной схемой линейно деформируемого слоя грунта, подстилаемого несжимаемым основанием.

Основная трудность при использовании этого метода заключается в том, что не всегда точно удается установить мощность сжимаемого слоя.

50. Расчет гибких фундаментов с помощью метода местных деформаций .

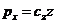
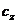
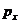
Предпосылкой расчёта гибких фундаментных балок по этому методу является гипотеза о том, что осадка в данной точке основания не зависит от осадки других точек и прямо пропорциональна давлению в этой точке (гипотеза Фусса — Винклера), что выражается зависимостью: , где — кэф пропорциональности, называемый кэфом постели, ориентировочно равный 0.3-1* кН/м3 при очень слабых грунтах, 1-3* при грунтах средней плотности, z – осадка в точке определения реакции .

Получаем дифференциальное уравнение изгиба балок на упругом основании по методу местных упругих деформаций:

Решение этого уравнения имеет вид:

где х – текущая координата; z – прогиб балки в точке с координатой х;

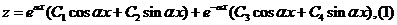
b – ширина фундаментной балки.

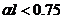
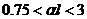
Кэф альфа – линейная характеристика балки на упругом основании. При , где l – длина фундаментной балки, балки классифицируются как короткие жёсткие, деформациями изгиба которых можно пренебречь; при — как короткие гибкие, при альфа эль больше 3 – длинные гибкие.

Постоянные интегрирования С1, С2, С3, С4 определяются из начальных условий деформирования, которые зависят от категории гибкости балки. Так, одним из начальных условий деформирования для короткой жёсткой балки, загруженной в центре сосредоточенной силой, будет постоянство деформации грунта вдоль всей её длины, а в случае длинной гибкой балки при таком же загружении начальным условием деформирования будет отсутствие прогиба на её концах.

Беря последовательно производные от выражения (1), определяют необходимые для конструирования фундаментной балки значения изгибающих моментов Мх и поперечных сил Qx в различных её сечениях. Если уточнённые по известным значениям Мх и Qx размеры балки значительно меняют её жёсткость, то расчёт повторяется.

Модель местных упругих деформаций рекомендуется применять для расчёта гибких фундаментных балок, работающих в условиях плоской задачи на сильносжимаемых грунтах (Е

Источник