Расчет изгибающего момента для фундамента

6.5. РАСЧЕТ ПЛИТНЫХ И ЛЕНТОЧНЫХ ФУНДАМЕНТОВ ПОД КОЛОННЫ

6.5.1. Общие положения

Расчет ленточных и плитных фундаментов, работающих на изгиб, проводится с учетом совместной работы конструкции и грунтового основания согласно теории конструкций на упругом основании. В этом случае предположение о линейном распределении реактивных давлений уже не может рассматриваться как достаточно точное, так как изгиб конструкции изменяет распределение этих давлений и, следовательно, отражается и на усилиях в балках и плитах. Линейное распределение давлений используется лишь для предварительного определения сечений конструкций.

6.5.2. Предварительное назначение размеров сечений

Предварительное назначение размеров сечений рассмотрим на примере ленточного фундамента под колонны, исходя из схемы линейного распределения реактивных давлений. Изгибающие моменты в каждом сечении ленты определяются по формуле

где M_l — момент в данном сечении от площади эпюры реактивных давлений, расположенной левее данного сечения; ΣP_il_i — сумма моментов для данного сечения от нагрузок, передаваемых колоннами, расположенными левее сечения (здесь Р_i — нагрузка от колонны i ; l_i —расстояние от колонны до сечения); ΣМ_i — сумма внешних моментов, передаваемых колоннами, расположенными левее данного сечения.

За положительное направление моментов принимается направление по часовой стрелке.

Таким образом, изгибающие моменты определяются простейшим способом по схеме статически определяемой балки. Не рекомендуется пользоваться расчетом статически неопределимой неразрезной балки, нагруженной трапецеидальной эпюрой давлений, при котором опорные реакции оказываются отличными от расчетных нагрузок, передаваемых на балку колоннами; кроме того, такой расчет сложнее. Использование схемы неразрезной балки оправдано лишь в случае, если жесткость верхнего строения очень велика и не позволяет смещаться опорным точкам колонн нелинейно относительно друг друга. В этом случае учитывается перераспределение внешней нагрузки по колоннам исходя из учета жесткости верхнего строения.

6.5.3. Расчет фундаментных балок и плит как конструкций на упругом основании

Для учета влияния изгиба на распределение реактивных давлений используется одно из двух предположений.

1. Основание работает согласно гипотезе коэффициента постели (Винклера). Эта гипотеза предполагает, что осадка какой-либо точки (элемента) поверхности основания s пропорциональна давлению р , приложенному в той же точке, т.е. что p = k_ss . Коэффициент k_s , Па/м, называется коэффициентом постели. Осадка данной точки (элемента) зависит только от давления, приложенного в этой точке, и не зависит от давлений, действующих по соседству (рис. 6.32, а).

2. Основание работает как среда, к которой применимы формулы теории упругости, связывающие напряжения и осадки. Грунт принимается за однородное упругое тело, бесконечно простирающееся вниз и в стороны и ограниченное сверху плоскостью (упругое полупространство), а соответствующее предположение называется гипотезой упругого полупространства. Поверхность упругого полупространства деформируется не только непосредственно под нагрузкой, но и по соседству с ней (рис. 6.32, б). Деформационные свойства грунта характеризуются в основном модулем деформации Е₀ , МПа.

Согласно гипотезе коэффициента постели, грунт лишен распределительной способности, т.е. деформации соседних с нагрузкой элементов поверхности грунта отсутствуют. Коэффициент постели для данного типа основания предполагается величиной, не зависящей от площади фундамента (в действительности — зависит).

В гипотезе упругого полупространства распределительная способность преувеличена. Модуль деформации является характеристикой, представляющей одновременно как упругие, так и остаточные деформации. При многократном приложении нагрузки остаточные деформации исчезают, модуль общей деформации Е₀ переходит в модуль упругости Е , значительно больший, чем Е₀ , При ширине фундамента примерно от 70 см до 7 м значение модуля деформации меняется незначительно. При превышении ширины 7 м модуль деформации заметно возрастает.

6.5.4. Связь между расчетными значениями модуля деформации и коэффициента постели

Между расчетными значениями модуля деформации Е₀ и коэффициентом постели, исходя из приравнивания осадок, вычисленных по той и другой гипотезе, устанавливается связь

Значение k₀ определяется по рис. 6.33 в зависимости от отношения сторон прямоугольного фундамента α, его опорной площади А и коэффициента Пуассона грунта ν₀ , принимаемого для песков ν₀ = 0,3, для суглинков и супесей ν₀ = 0,35, для глин ν₀ = 0,4.

Осадки жесткого прямоугольного фундамента на однородном основании определяются по формуле

где Р — суммарная центрированная нагрузка на фундамент.

Осадки жесткой плиты лишь немного меньше (на 7 %) средних осадок гибкой плиты при равномерной нагрузке.

Расчеты по обеим гипотезам, даже при использовании формулы (6.126), дают, как правило, различные результаты в отношении изгибающих моментов в конструкции и ее изгиба. Только для узких балок при α ≥ 10 можно подобрать отличное от определяемого формулой (6.127) значение коэффициента постели, при котором результаты расчета будут близки. Однако при равномерной нагрузке или при нагрузке, приближающейся к ней, получить близкие результаты расчета при любом соотношении между E₀ и k невозможно. Формула соотношения между Е₀ и k , для узких балок шириной В имеет вид:

Гибкие фундаменты в настоящее время рассчитываются преимущественно по гипотезе упругого полупространства. Этот расчет при фундаментах большой опорной площади, в десятки или сотни квадратных метров, дает, однако, преувеличенное значение осадки, изгиба и изгибающих моментов, так как гипотеза игнорирует уплотнение грунта с глубиной, вызванное действием его собственного веса. Кроме того, при больших опорных площадях грунт под фундаментом сжимается в основном без возможности бокового расширения, что не учитывается при опытном определении модуля деформации штампом.

Чтобы приблизить расчетные условия к действительным, при больших опорных площадях используют схему, согласно которой основание представляет собой сжимаемый слой, подстилаемый несжимаемым основанием. Удобно также использовать схему однородного полупространства с повышенным модулем деформации так, чтобы расчет по этой схеме давал значение, равное ожидаемой осадке.

Сорочан Е.А. Основания, фундаменты и подземные сооружения

Источник

К расчету балок на упругом основании

В малоэтажном строительстве, как впрочем и в любом другом, балки на упругом основании встречаются намного чаще, чем это можно подумать. По той причине, что любой ленточный фундамент, а иногда и плитный фундамент можно рассматривать как балку на упругом основании.

И если с расчетом балки — ленточного фундамента проблем практически не возникает по той простой причине, что нагрузка на ленточный фундамент как правило равномерно распределенная, а значит и фундамент ведет себя, как абсолютно жесткая балка, дополнительных расчетов не требующая. То при рассмотрении участка плитного фундамента как балки или ленточного фундамента с неравномерно приложенной нагрузкой могут возникнуть некоторые проблемы.

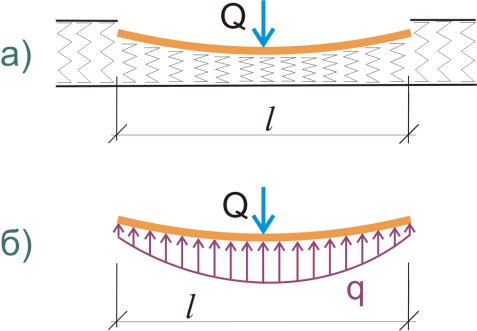
Дело в том, что на сегодняшний день не существует идеальной модели упругого основания. Одной из наиболее распространенных является модель Фусса-Винклера, согласно которой опорная реакция упругого основания, другими словами — распределенная нагрузка q, действующая на балку, является не равномерно распределенной, а пропорциональной прогибу балки f в рассматриваемой точке:

q = — kf (393.1)

k = k_оb (393.2)

k_о — коэффициент постели, постоянный для рассматриваемого основания и характеризующий его жесткость, измеряется в кгс/см 3 .

b — ширина балки.

Рисунок 393.1 а) модель балки на сплошном упругом основании, б) реакция основания q на действующую сосредоточенную нагрузку.

Из этого можно сделать как минимум два вывода, неутешительных для человека, собравшегося по-быстрому рассчитать фундамент небольшого домика, к тому же даже основы теоретической механики и теории сопротивления материалов постигшего с трудом:

1. Расчет балки на упругом основании — это статически неопределимая задача, так как уравнения статики позволяют лишь определить суммарное значение нагрузки q (реакции основания). Распределение нагрузки по длине балки будет описываться достаточно сложным уравнением:

q/EI = d 4 f/dx 4 + kf/EI (393.3)

которое мы здесь решать не будем.

2. Помимо всего прочего при расчете таких балок необходимо знать не только коэффициент постели основания, но и жесткость балки ЕI, т.е. все параметры балки — материал, ширина и высота сечения, должны быть известны заранее, между тем при расчете обычных балок определение параметров и является основной задачей.

И что в этом случае делать простому человеку, не обремененному глубокими знаниями сопромата, теорий упругости и прочих наук?

Ответ простой: заказать инженерно-геологические изыскания и проект фундамента в соответствующих организациях. Да, я понимаю, что при этом стоимость дома может увеличиться на несколько тысяч $, но все равно это оптимальное решение в таком случае.

Если же вы, не смотря ни на что, хотите сэкономить на геологоразведке и расчете, т.е. выполнить расчет самостоятельно, то будьте готовы к тому, что придется больше средств потратить на фундамент. Для такого случая я могу предложить следующие расчетные предпосылки:

1. Как правило сплошная фундаментная плита принимается в качестве фундамента в тех случаях, когда несущая способность основания очень низкая. Другими словами грунт — это песок или глина, никак не скальные породы. Для песка, глины и даже гравия коэффициент постели, определенный опытным путем в зависимости от различных факторов (влажности, крупности зерен и др.) k_o = 0.5-5 кгс/см 3 . Для скальных пород k_o = 100-1500 кг/см 3 . Для бетона и железобетона k_o = 800-1500 кгс/см 3 . Как видно из формулы 393.1, чем меньше значение коэффициента постели, тем больше будет прогиб балки при той же нагрузке и параметрах балки. Таким образом мы можем для упрощения дальнейших расчетов предположить, что слабые грунты не влияют на прогиб балки, точнее этим незначительным влиянием можно пренебречь. Другими словами изгибающие моменты, поперечные силы, углы поворотов поперечных сечений и прогибы будут такими же, как и у балки, загруженной распределенной нагрузкой. Результатом такого допущения будет повышенный запас прочности и чем больше будут прочностные характеристики грунтов, тем большим будет запас прочности.

2. Если сосредоточенные нагрузки на балку будут симметричными, то для упрощения расчетов реакцию упругого основания можно принимать равномерно распределенной. Основанием для такого допущения служат следующие факторы:

2.1. Как правило фундамент, рассматриваемый как балка на упругом основании, в малоэтажном строительстве имеет относительно небольшую длину — 10-12 м. При этом нагрузка от стен, рассматриваемая как сосредоточенная, в действительности является равномерно распределенной на участке, равном ширине стен. Кроме того балка имеет некоторую высоту, на первом этапе расчета не учитываемую, а между тем даже сосредоточенная нагрузка, приложенная к верху балки, будет распределяться в теле балки и чем больше высота балки, тем больше площадь распределения. Так например для фундаментной плиты высотой 0.3 м и длиной 12 м, рассматриваемой как балка, на которую опираются три стены — две наружных и одна внутренняя, все толщиной 0.4 м, нагрузки от стен более правильно рассматривать не как сосредоточенные, а как равномерно распределенные на 3 участках длиной 0.4 + 0.3·2 = 1 м. Т.е. нагрузка от стен будет распределена на 25% длины балки, а это не мало.

2.2. Если балка лежащая на сплошном упругом основании имеет относительно небольшую длину и к ней приложено несколько сосредоточенных нагрузок, то реакция основания будет изменяться не от 0 в начале длины балки до некоего максимального значения посредине балки и опять до 0 в конце длины балки (для варианта показанного на рис. 393.1), а от некоторого минимального значения до максимального. И чем больше сосредоточенных нагрузок будет приложено к балке относительно небольшой длины, тем меньше будет разница между минимальным и максимальным значением опорной реакции упругого основания.

Результатом принятого допущения будет опять же некоторый запас прочности. Впрочем в данном случае возможный запас прочности не превысит нескольких процентов. Например, даже для однопролетной балки, на которую действует распределенная нагрузка, равномерно изменяющая от 1.5q в начале балки до 0.5q в середине балки и снова до 1.5q в конце балки (см. статью «Приведение распределенной нагрузки к эквивалентной равномерно распределенной») суммарная нагрузка составит ql, как и для балки, на которую действует равномерно распределенная нагрузка. Между тем максимальный изгибающий момент для такой балки составит

М = ql 2 /(8·2) + ql 2 /24 = 10ql 2 /96 = ql 2 /9.6

Это на 20% меньше, чем для балки, на которую действует равномерно распределенная нагрузка. Для балки, изменение опорной реакции которой описывается достаточно сложным уравнением, особенно если сосредоточенных нагрузок будет много, разница будет еще меньше. Ну и не забываем про п.2.1.

В итоге при использовании данных допущений задача расчета балки на сплошном упругом основании максимально упрощается, особенно при симметричности приложенных нагрузок, несимметричные нагрузки приведут к крену фундамента и этого в любом случае следует избегать. Более того на расчет практически не влияет количество приложенных сосредоточенных нагрузок. Если для балки на шарнирных опорах вне зависимости от их количества должно соблюдаться условие нулевого прогиба на всех опорах, что увеличивает статическую неопределимость балки на количество промежуточных опор, то при расчете балки на упругом основании достаточно рассматривать прогиб, как нулевой, в точках приложения крайних сосредоточенных нагрузок — наружных стен. При этом прогиб под сосредоточенными нагрузками — внутренними стенами определяется согласно общих уравнений. Ну а определить осадку фундамента в точках, где прогиб принят нулевым, можно, воспользовавшись существующими нормативными документами по расчету оснований и фундаментов.

А еще можно достаточно просто подобрать длину консолей балки таким образом, чтобы прогиб и под внутренними стенами был нулевым. Пример того, как можно воспользоваться данными расчетными предпосылками, рассказывается отдельно.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Основы строймеха и сопромата . Балки

Оценка пользователей: Нет Переходов на сайт: 3356 Комментарии:

Добрый день! Пытаюсь рассчитать свой ленточный фундамент. Размеры в плане 10х10м. Ширина 0,4м Высота 1м. Равномерно распределенная нагрузка 5т/м Пытаюсь рассчитать продольную рабочею арматуру. Пользуюсь формулами из пособия по СП 52-101-2003 Там есть формула для нахождения Am. Для данной формулы необходимо найти изгибающий момент. Можно ли использовать вашу формулу для нахождения изг момента для балки на упругом оснвании М=q*lквадрат/9,6 На форумах говорят слишком уж большой момент будет.

Ваш вопрос достаточно сложный и я по этому поводу давно собираюсь написать соответствующую статью, но все руки не доходят. Поэтому попробую тезисно.
Вообще-то если нагрузка от здания равномерно распределенная, а физико-химические свойства основания постоянны, то никакого продольного армирования для ленточного фундамента не требуется (смотрите второй абзац).
Тем не менее и равномерно распределенная нагрузка и однородное основание возможны только в теории. На практике же основание состоит из различных пород, залегающих слоями, различной толщины и под различными углами, но даже в этих слоях свойства пород меняются. К тому же еще есть грунтовые воды, сезон замерзания и оттаивания, карстовые процессы и прочие неожиданности. Даже геологоразведка позволяет определить свойства основания лишь приблизительно. Да и нагрузка является равномерно распределенной достаточно условно. Поэтому армирование фундаментной стены никогда не помешает. А вот какую расчетную схему для этого выбрать — это отдельный вопрос. Принимая для расчета армирования нижней зоны поперечного сечения момент М=q*l^2/9,6, вы допускаете, что ваш ленточный фундамент будет иметь опоры только в углах (если рассматривать его как однопролетную балку), а под остальным фундаментом грунт или вымоется или просядет сильнее чем под углами. Что хотя теоретически и возможно, но все равно маловероятно, так как при этом нагрузки в углах — опорные реакции балки -возрастают значительно и значит грунт в углах тоже скорее всего просядет.
Если же вы будете использовать подобное значение момента для расчета армирования верхней зоны поперечного сечения фундамента, то это будет не совсем корректно, но для упрощения расчетов допустимо. Тем более, что чаще всего фундаменты проседают в углах зданий, что приводит к трещинам в стенах из материалов, плохо работающих на растяжение. Хотя и запас прочности при этом получится скорее всего не малый.
Кроме того подобные расчеты подразумевают, что бетонировать фундамент вы будете сразу, без технологических перерывов, чтобы обеспечить монолитность балки. Примерно так.

Спасибо за ответ! Если я правильно понимаю в расчете рабочей продольной арматуры все упирается в нахождении максимального изгибающего момента в фундаменте? Зная его можно пользоваться формулами из пособия к СП 52-101-2003. У вас расчет плиты перекрытия http://doctorlom.com/item220.html сделан по формулам из данного пособия. По ним и я хотел считать. Но для балок http://doctorlom.com/item170.html у вас другая методика расчета. Какую лучше использовать для расчета ленточного фундамента.

Оба метода построены на одних и тех же теоретических предпосылках и дают практически одинаковый результат. так что можете пользоваться тем, который вам больше нравится.

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник