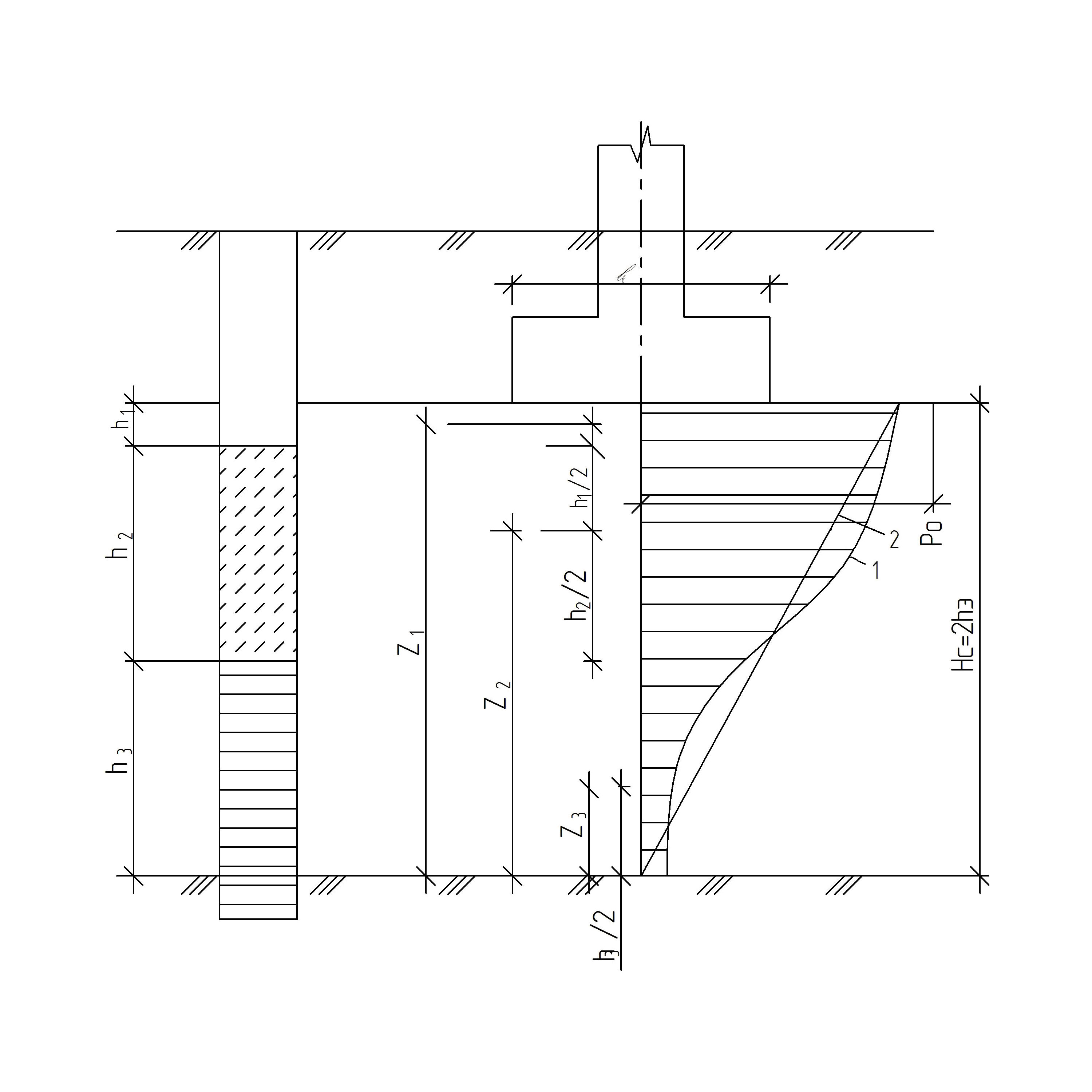
Расчёт конечной осадки фундамента методом эквивалентного слоя
Эквивалентным называется слой грунта мощностью hэ, осадка которого при сплошной нагрузке на поверхности pо будет равна осадке грунтового полупространства под воздействием местной нагрузки интенсивностью ро.
Осадка слоя грунта из условия одномерного сжатия без возможности бокового расширения 
где Е – модуль деформации грунта; v – коэффициент Пуассона.
Значение v принимаются в зависимости от вида и состояния грунтов:
— глины и суглинки твёрдой и полутвёрдой консистенции v = 0,1…0,15;
— то же тугопластичной v = 0,2…0,25;
— то же мягко пластичной и текучепластичной v = 0,3…0,4;
— то же текучей v = 0,45…0,5;
С учётом относительного коэффициента сжимаемости грунтов mv
β – коэффициент, зависящий от коэффициента Пуассона, т.е.

Толщина эквивалентного слоя hэ =Aωb, (6.5)
где: А– площадь подошвы фундамента; ω – коэффициент, зависящий от формы, площади и жёсткости фундамента, значения табулированы в табл. 3.
Значения коэффициентов ω для полупространства
| Отношение сторон n=ℓ/b | ωс | ωо | ωm | ωсоnst |
| 1-круг | 0,64 | 1,00 | 0,85 | 0,79 |
| 1-квадрат | 0,5 ωо | 1,12 | 0,95 | 0,88 |
| 2-прямоугольник | 0,5 ωо | 1,53 | 1,30 | 1,22 |
| 3- прямоугольник | 0,5 ωо | 1,78 | 1,53 | 1,44 |
| 4- прямоугольник | 0,5 ωо | 1,96 | 1,70 | 1,61 |
| 5 – прямоугольник | 0,5 ωо | 2,10 | 1,83 | 1,72 |
| 10 — прямоугольник | 0,5 ωо | 2,53 | 2,25 | 2,12 |
ωс – для осадки угловой точки прямоугольника или круга;
ωо – для максимальной осадки гибкого фундамента под центром загружаемой площади;
ωm – для средней осадки гибкого фундамента всей площади загружения;
ωсоnst – для осадки абсолютно жёстких фундаментов.
b – ширина подошвы фундамента.
Произведение Aω называется коэффициентом эквивалентного слоя, значения табулированы в табл. 4.
Значения коэффициента эквивалентного слоя Aω
| Соотнош. ℓ / b | Гравий и галька | Пески | Суглинки пластичные | Глины и суглинки мягкопластичные | ||||||||||||||
| Глины и суглинки твёрдые и полутвёрдые | Супеси твёрдые и пластичные | Глины пластичные | ||||||||||||||||
| v = 0,10 | v = 0,20 | v = 0,25 | v = 0,30 | v = 35 | v = 40 | |||||||||||||
| 1,0 | 1,13 | 0,96 | 0,89 | 1,20 | 1,01 | 0,94 | 1,26 | 1,07 | 0,99 | 1,37 | 1,17 | 1,08 | 1,58 | 1,34 | 1,24 | 2,02 | 1,71 | 1,58 |
| 1,5 | 1,37 | 1,16 | 1,09 | 1,45 | 1,23 | 1,15 | 1,53 | 1,30 | 1,21 | 1,66 | 1,40 | 1,32 | 1,91 | 1,62 | 1,52 | 2,44 | 2,07 | 1,94 |
| 2,0 | 1,55 | 1,31 | 1,23 | 1,63 | 1,39 | 1,30 | 1,72 | 1,47 | 1,37 | 1,88 | 1,60 | 1,49 | 2,16 | 1,83 | 1,72 | 2,76 | 2,34 | 2,34 |
| 3,0 | 1,81 | 1,55 | 1,46 | 1,90 | 1,63 | 1,54 | 2,01 | 1,73 | 1,62 | 2,18 | 1,89 | 1,76 | 2,51 | 2,15 | 2,01 | 3,21 | 2,75 | 2,59 |
| 4,0 | 1,99 | 1,72 | 1,63 | 2,09 | 1,81 | 1,72 | 2,21 | 1,92 | 1,81 | 2,41 | 2,09 | 1,97 | 2,77 | 2,39 | 2,26 | 3,53 | 3,06 | 2,90 |
| 5,0 | 2,13 | 1,85 | 1,74 | 2,24 | 1,95 | 1,84 | 2,37 | 2,07 | 1,94 | 2,58 | 2,25 | 2,11 | 2,96 | 2,57 | 2,42 | 3,79 | 3,29 | 3,10 |
| 6,0 | 2,25 | 1,98 | — | 2,37 | 2,09 | — | 2,50 | 2,21 | — | 2,72 | 2,41 | — | 3,14 | 2,76 | — | 4,00 | 3,53 | — |
| 7,0 | 2,35 | 2,06 | — | 2,47 | 2,18 | — | 2,61 | 2,31 | — | 2,84 | 2,51 | — | 3,26 | 2,87 | — | 4,18 | 2,67 | — |
| 8,0 | 2,43 | 2,14 | — | 2,56 | 2,26 | — | 2,70 | 2,40 | — | 2,94 | 2,61 | — | 3,38 | 2,98 | — | 4,32 | 3,82 | — |
| 9,0 | 2,51 | 2,21 | — | 2,64 | 2,34 | — | 2,79 | 2,47 | — | 3,03 | 2,69 | — | 3,49 | 3,08 | — | 4,46 | 3,92 | — |
| 10 и более | 2,58 | 2,27 | 2,15 | 2,71 | 2,40 | 2,26 | 2,86 | 2,54 | 2,38 | 3,12 | 2,77 | 2,60 | 3,58 | 3,17 | 2,98 | 4,58 | 4,05 | 3,82 |
| Коэфф. | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst | Аωо | Аωm | Аωсоnst |
Для однородного основания требуемая осадка при известных E и ν определяется по формуле (6.2).
Для слоистого основания осадка

где: mv – средневзвешенный относительный коэффициент сжимаемости

который определяется с использованием расчётной эпюры на рис. 14.
Рис. 14. Схема к определению осадок методом эквивалентного слоя для многослойного основания:
1 – расчётная нелинейная эпюра дополнительных напряжений;
2 – эквивалентная треугольная эпюра дополнительных напряжений.
Средневзвешенное значение коэффициента Пуассона

где Нс – мощность сжимаемой толщи основания
Пример расчёта:
Определить методом эквивалентного слоя осадку столбчатого фундамента, рассчитанного в п.п. 6.1 и 6.2,
Р о = Р — 
Грунтовые условия – по заданию.
II слой – песок мелкий, средней плотности с коэффициентом Пуассона ν=0,2.
При глубине заложения фундамента 3,05 м
h = 5.5 – 3.05 = 2,45 м
По табл. 4 определяем Аωm=1,01.
Толщина эквивалентного слоя
Мощность сжимаемой толщи
При глубине заложения подошвы фундамента d=3,05 м в сжимаемую толщу входит II и III слои грунтов с модулями деформаций ЕI I =28 МПа,
Относительные коэффициенты сжимаемости для:
— второго слоя при νI I = 0,2; 

— третьего слоя ( глина пылеватая, комковая, полутвердая)
νI I I = 0,12; 
— средний относительный коэффициент сжимаемости
Конечная осадка фундамента

Источник
Расчет осадки методом эквивалентного слоя
Метод эквивалентного слоя дает возможность упростить технику расчета конечных осадок и их развития во времени.
Данный метод предусматривает следующие основные допущения:
— грунт однороден в пределах полупространства;
— грунт представляет собой линейно деформируемое тело;
— деформации грунта в пределах полупространства принимаются по теории упругости.
Эквивалентным слоем называется такой слой грунта толщиной hэ , осадка которого при сплошной нагрузке на поверхности Р будет равна осадке грунтового полупространства под воздействием местной нагрузки той же интенсивности.
В методе эквивалентного слоя конечную осадку фундамента определяют в результате решения задачи теории упругости полупространства под действием равномерно распределенной нагрузки по формуле

где mv — коэффициент относительной сжимаемости грунта;
Р — давление под подошвой фундамента;
hэ — мощность эквивалентного слоя грунта, вычисляемая по формуле

где 

А — коэффициент, зависящий от коэффициента бокового расширения

где 
Произведение 
Для расчета осадки фундамента при слоистом залегании грунтов в основании эпюру напряжений 
Осадку слоистого основания вычисляют также по формуле (71) с той лишь разницей, что в ней вместо коэффициента относительной сжимаемости mv используют средний коэффициент относительной сжимаемости mvm, вычисляемый по формуле

где 





По этому методу, кроме конечной осадки, можно определить затухание осадки во времени, что значительно расширяет пределы его применяемости.
  | Гравий и галька | Пески | Суглинки пластичные | Глины и суглинки | |
| Глины и суглинки твердые и полутвердые | Супеси твердые и пластичные | Глины пластичные | Мягкоплас- тичные | ||
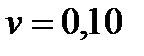 |  |  |  |  |  |
| 1.0 | 1.13 | 0,96 | 0,89 | 1,20 | 1.01 | 0,94 | 1,26 | 1,07 | 0,99 | 1,37 | 1.17 | 1,08 | 1,58 | 1.34 | 1.24 | 2,02 | 1.71 | 1.58 |
| 1.5 | 1,37 | 1,16 | 1,09 | 1.45 | 1.23 | 1.15 | 1,53 | 1,30 | 1.21 | 1,66 | 1.40 | 1,32 | 1,91 | 1,62 | 1.52 | 2,44 | 2.07 | 1,94 |
| 2.0 | 1,55 | 1,31 | 1,23 | 1,63 | 1,39 | 1,30 | 1,72 | 1.47 | 1.37 | 1,88 | 1,60 | 1,49 | 2,16 | 1,83 | 1,72 | 2,76 | 2,34 | 2 20 |
| 3.0 | 1.81 | 1,55 | 1,46 | 1,90 | 1.63 | 1,54 | 2,01 | 1.73 | 1,62 | 2.18 | 1,89 | 1.76 | 2,51 | 2,15 | 2,01 | 3,21 | 2,75 | 2,59 |
| 4.0 | 1,99 | 1.72 | 1,63 | 2,09 | 1,81 | 1.72 | 2,21 | 1,92 | 1.81 | 2,41 | 2,09 | 1,97 | 2.77 | 2,39 | 2,26 | 3,53 | 3,06 | 2,90 |
| 5.0 | 2.13 | 1,85 | 1.74 | 2.24 | 1,95 | 1,84 | 2,37 | 2,07 | 1.94 | 2.58 | 2,25 | 2,11 | 2,96 | 2,57 | 2,42 | 3,79 | 3,29 | 3,10 |
| 6.0 | 2.25 | 1,98 | — | 2,37 | 2,09 | — | 2,50 | 2,21 | — | 2,72 | 2,41 | — | 3.14 | 2,76 | — | 4,00 | 3,53 | — |
| 7.0 | 2.35 | 2,06 | — | 2.47 | 2,18 | — | 2,61 | 2,31 | — | 2,84 | 2,51 | — | 3,26 | 2,87 | — | 4,18 | 2,67 | — |
| 8.0 | 2.43 | 2.14 | — | 2,56 | 2,26 | — | 2,70 | 2,40 | — | 2,94 | 2,61 | — | 3,38 | 2,98 | — | 4,32 | 3,82 | — |
| 9.0 | 2.51 | 2,21 | — | 2,64 | 2,34 | — | 2,79 | 2,47 | — | 3,03 | 2,69 | — | 3,49 | 3,08 | — | 4,46 | 3,92 | — |
| 10 и более | 2,58 | 2,27 | 2.15 | 2.71 | 2,40 | 2,26 | 2,86 | 2,54 | 2,38 | 3,12 | 2.77 | 2,60 | 3,58 | 3,17 | 2,98 | 4,58 | 4,05 | 3,82 |
| Коэффи- циенты | Аω0 | Аωm | АωСonst | Аω0 | Аωm | АωСonst | Аω0 | Аωm | АωСonst | Аω0 | Аωm | АωСonst | Аω0 | Аωm | АωСonst | Аω0 | Аωm | АωСonst |
Рис. 22. Схема к определению осадок методом эквивалентного слоя
Значения коэффициента эквивалентного слоя
Примечание: Аω0 — для осадки под центром тяжести гибкого фундамента;
Аωm — для средней осадки фундамента конечной жесткости;
АωСonst — для осадки абсолютно жесткого фундамента.
Изменение осадок во времени
В соответствии с фильтрационной теорией консолидации осадку, происходящую за время 

где S — конечная осадка, определенная методом эквивалентного слоя по формуле (71);
U — степень уплотнения (консолидации), представляющая собой долю от полной осадки за время t.
Степень консолидации U определяют из выражения

где N — постоянный множитель. Определяется по формуле

где 

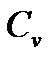

где Кф — коэффициент фильтрации грунта;
mv — коэффициент относительной сжимаемости;

В случае слоистого напластования грунтов основания определяют осредненное значение коэффициента фильтрации в пределах сжимаемой толщи по формуле

и коэффициента консолидации по формуле

а осредненное значение коэффициента относительной сжимаемости mvm — по формуле (74).
Учитывая выражения (71) и (76), получим для случая равномерного распределения уплотняющих давлений по глубине осадку для любого времени t:

Для облегчения расчетов в табл. 11 приведены значения 
Значение e — x в зависимости от х
Источник