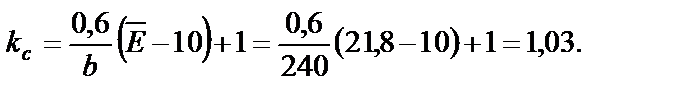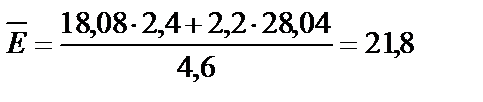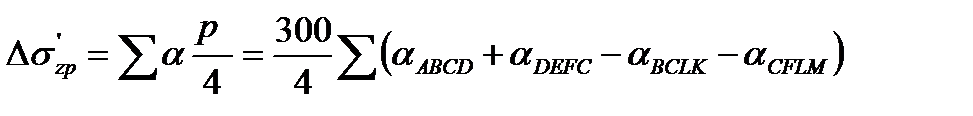Пример 3. Расчет осадки с учетом влияния соседнего фундамента (метод угловых точек).
Задание: Рассчитать осадку фундамента (пример 2) с учетом влияния фундамента под колонну. Размеры подошвы влияющего фундамента 
м, давление по подошве влияющего фундамента 300 кПа. Расстояние между осями ленточного и отдельно стоящего фундамента 3м
Решение:
Проверка выполнения условия, при котором необходимо учитывать влияние соседнего фундамента:
,
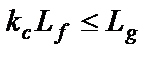
где 
Где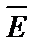 
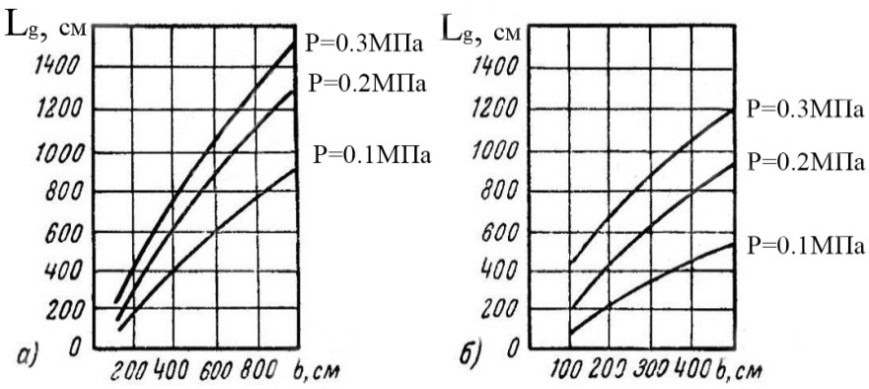
– осредненный модуль деформации в пределах сжимаемой зоны
По графикам (рис.4,б) Lg=3,6м, фактическое расстояние Lf=3м. Условие выполняется, необходимо учитывать влияние соседнего фундамента.
Рис. 4. Графики для определения расстояния между осями фундаментов, при котором учитывается взаимное влияние:
a – для квадратного фундамента; б – для прямоугольного фундамента
Напряжения от влияющего фундамента учитываются методом угловых точек.
Пользуясь методом угловых точек, можно найти напряжение в любой точке полупространства, к поверхности которого приложена равномерно распределенная нагрузка в пределах прямоугольной площади. Метод угловых точек для определения сжимающих напряжений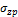 
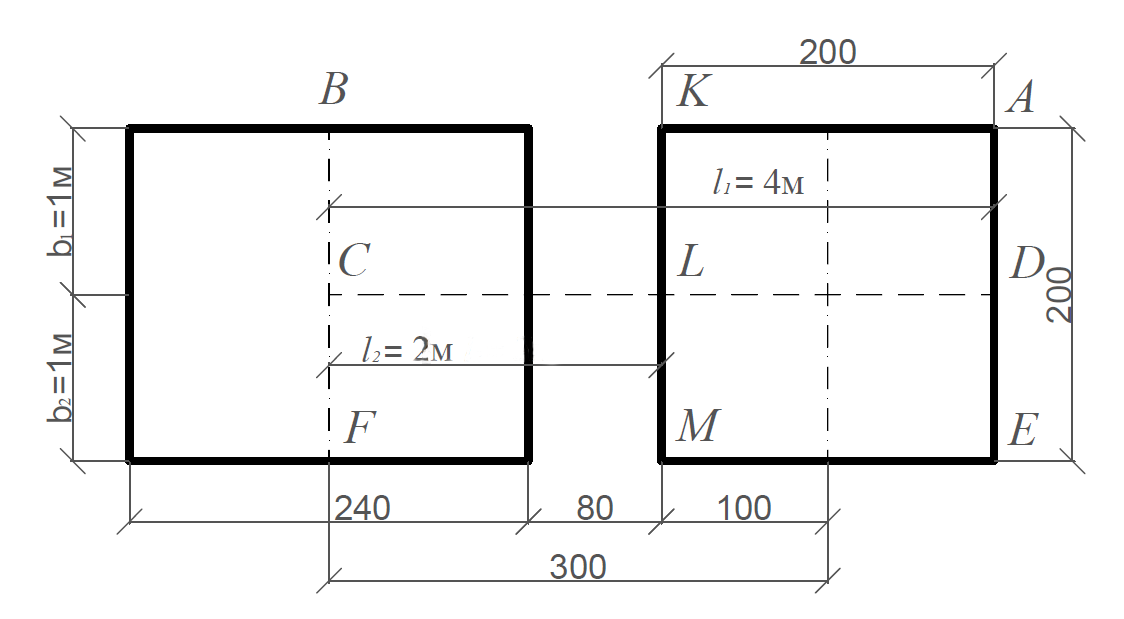
применяют в случае, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась угловой. Тогда сжимающее напряжение в этой точке на любой глубине будет равно алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.
Если точка С лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой. Тогда, полагая, что напряжения в точке С возникают от действия нагрузки, распределенной по площади прямоугольников ABCD и DEFC, необходимо вычесть напряжения от действия фиктивной нагрузки, распределенной по площади прямоугольников BCLK и CFML (рис.5).
Для точек, расположенных по вертикальной оси под центром загруженного прямоугольника, сжимающие напряжения
(3.1)
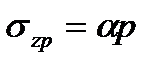
Рис. 5. К расчету дополнительных напряжений методом угловых точек
А для точек, расположенных по вертикальной оси под углом загруженного прямоугольника,
, (3.2)
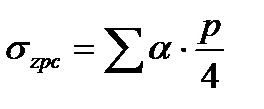
где α – коэффициент, принимаемый по табл.12 в зависимости от соотношения сторон η = l/b прямоугольной нагрузки (формы подошвы фундамента) и относительной глубины, равной: ξ = 2z/b – при определении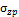 
. 
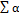
– сумма коэффициентов по табл.12 в зависимости от η = l/b, и относительной глубины ξ = z/b, 
– давление по подошве влияющего фундамента.
Определение дополнительных напряжений сведено в таблицу.
Значения дополнительных напряжений ∆σzp суммируются с основными σzp и служат для расчета осадок.
Источник
Определение осадки фундамента с учетом соседних фундаментов
Определим осадку от основного фундамента, который находится на оси «Г6», с учетом влияния на нее ближайших фундаментов, а именно, соседних фундаментов на расстоянии 6 и 12 метров от основного.
Для его определения следует отдельно определить осадку от основного фундамента, и дополнительную осадку, вследствии влияния соседних фундаментов.
Определим осадку от основного фундамента, для этого рассмотрим формулу:
;
Коэффициент Ko определяется по формуле:
=0,996 – так как b = l = 2,1 метра.
Определим бытовое давление на уровне подошвы фундамента :
p = pII = 314,27 кПа;
Найдем осадку первого слоя под подошвой фундамента:
;
;
;
Найдем осадку второго слоя под подошвой фундамента:
;
;
;
Найдем общую осадку от основного фундамента, находящегося на оси «Г6»:
Sпр общ = Sпр1+Sпр2= 2,7+2,22=4,92 см; — осадка основного фундамента.
Рассчитаем осадку от соседних фундаментов находящихся на расстоянии 6 метров (х = 6 метров) от основного фундамента на оси «Г6», для этого рассмотрим формулу:
;
Найдем величины 
и 
:
;
;
;
Тогда осадка первого слоя от соседнего фундамента на расстоянии 6 метров равна:
= 
;
;
Найдем величины и :
;
;
;
Тогда осадка второго слоя от соседнего фундамента на расстоянии 6 метров равна:
= 
;
Итого получаем, что влияние на осадку одного соседнего фундамента на расстоянии 6 метров равна:
Тогда влияние на осадку двух соседних фундаментах равен:
Sоб.д.6м = 2*Sдоп 6м = 2*0,1345= 0,269 мм.
Рассчитаем осадку от соседних фундаментов находящихся на расстоянии 12 метров (х = 12 метров) от основного фундамента на оси «Г6», для этого рассмотрим формулу:
;
Найдем величины и :
;
;
;
Тогда осадка первого слоя от соседнего фундамента на расстоянии 12 метров равна:
= 
;
;
Найдем величины и :
;
;
;
Тогда осадка второго слоя от соседнего фундамента на расстоянии 6 метров равна:
= 
;
Итого получаем, что влияние на осадку одного соседнего фундамента на расстоянии 12 метров равна:
Sдоп 12 м =Sдоп1+ Sдоп2=0,001558+0,006995=0,008553 мм.
Тогда влияние на осадку двух соседних фундаментах равен:
Sоб.д.12м = 2*Sдоп 12м = 2*0,008553= 0,017 мм.
Рассчитаем осадку от соседних фундаментов находящихся на расстоянии 18 метров (х = 18 метров) от основного фундамента на оси «Г6», для этого рассмотрим формулу:
;
Найдем величины и :
;
;
;
Тогда осадка первого слоя от соседнего фундамента на расстоянии 18 метров равна:
= 
;
;
Найдем величины и :
;
;
;
Тогда осадка второго слоя от соседнего фундамента на расстоянии 8 метров равна:
= 
;
Итого получаем, что влияние на осадку одного соседнего фундамента на расстоянии 18 метров равна:
Sдоп 18 м =Sдоп1+ Sдоп2 = 0+0,00106 = 0,00106 мм.
Тогда влияние на осадку двух соседних фундаментах равен:
Sоб.д.18м = 2*Sдоп 18м = 2*0,00106= 0,00212 мм.
Вследствии довольно малой величины осадки( в процентном соотношении к осадке соседнего фундамента ≈0,00431%), мы можем сделать вывод, что влияние соседних фундаментов на расстоянии 18 метров можно не учитывать.
Тогда, общая осадка основного фундамента на оси «Г6» с учетом соседних фундаментов на расстоянии 6 и 12 метров равен:
Sобщ = S пр общ+ Sобщ.д. 6м+Sобщ.д. 12м= 49,2 + 0,269 + 0,017=49,486 мм = 4,949 см;
Проверяем основное условие расчет оснований по деформациям, По СНиП 2.02.01—83* для зданий данного типа находим предельно допустимую осадку Su = 20 см.
Источник