Расчет простенка внутренней стены

Содержание

4. Расчет внутреннего простенка.
Расчет по сечению 4-4
Проверка по сечению 5-5
Расчет простенка внутренней стены
Расчет простенка для каменных конструкций

4. Расчет внутреннего простенка.

Для расчета выберем простенок шириной 1м + половина дверного проема 0.45м.

Сечение простенка прямоугольное с размерами h*b = 0,38*1,00=0,38 м 2 .

Грузовая площадь для расчета внутренней стены А_гр2=6,0*1,45=8,7 м 2 .

4.1 Расчет внутреннего простенка на первом этаже.

При определении равномерно распределенных нагрузок для жилых помещений принимаем коэффициент сочетания равный [1, формулы 1 и 3]:

Где А=8,7м 2 , А₁=9м 2 n=8–общее число перекрытий, нагрузки от которых учитываются при расчете рассматриваемого сечения стены.

Так как А = 8,7 м 2 2 , то Ψ_А1 = 1,

Расчет по сечению 4-4

Расчетное усилие от вышележащих конструкций

1) собственный вес стены вышележащих этажей:

γ=1800кг/м 3 =18кН/ м 3 -удельный вес кладки

кН, где

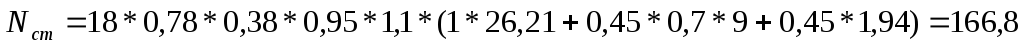
γ_f=1,1 – коэффициент надежности по нагрузке для собственного веса стены [1, табл. 1].

2) собственный вес покрытия

кН.

3) сосредоточенная сила от перекрытия

4) перекрытия вышележащих этажей

N_пер tot =7*8,7*(4,967+1,95*0,61)*0,95=356,184 кН

5) чердачное перекрытие

φ – коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый по расчетной высоте элемента l₀;

1) расчетная высота элемента равна [2, п. 4.3, примечание а]:

м;

2) гибкость элемента для прямоугольного сплошного сечения равна [2, п. 4.2]:

;

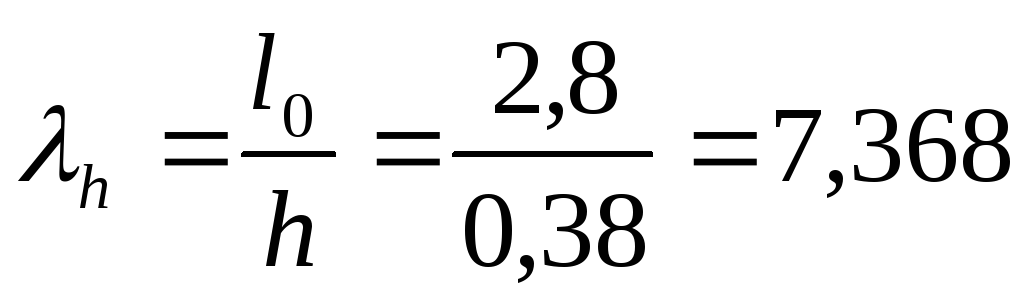
3) упругая характеристика кирпича α=1000 [2, табл.15], согласно табл. 18 [2] ;

При h=0,38 м > 0,3м m_g=1 – коэффициент, учитывающий влияние длительной нагрузки [2, п. 4.7].

Тогда расчетное сопротивление:

R =689,33/(1*0,933*0,38)=1944,29 кН/м 2 = 1,944 МПа;

По таблице 2 [2] принимаем марку кирпича 125 и марку раствора 100 (R=2,0МПа).

Проверка по сечению 5-5

Расчетное усилие от вышележащих конструкций

1) собственный вес стены вышележащих этажей:

γ=1800кг/м 3 =18кН/ м 3 -удельный вес кладки

кН, где

γ_f=1,1 – коэффициент надежности по нагрузке для собственного веса стены [1, табл. 1].

2) собственный вес покрытия

кН.

3) сосредоточенная сила от перекрытия

4) перекрытия вышележащих этажей

N_пер tot =7*8,7*(4,967+1,95*0,61)*0,95=356,184 кН

5) чердачное перекрытие

Для сечения 5-5 φ=1

При h=0,38 м > 0,3м m_g=1 – коэффициент, учитывающий влияние длительной нагрузки [2, п. 4.7].

Проверка несущей способности простенка:

Несущая способность простенка обеспечена, т.е. марка кирпича и марка раствора были подобраны верно.

4.2 Расчет внутреннего простенка на пятом этаже.

Сечение простенка прямоугольное с размерами h*b = 0,38*1,00=0,38 м 2 .

Грузовая площадь для расчета внутренней стены А_гр2=6,0*1,45=8,7 м 2 .

Где А=8,7м 2 , А₁=9м 2 n=4–общее число перекрытий,нагрузки от которых учитываются при расчете рассматриваемого сечения стены.

Так как А = 8,7м 2 2 , то Ψ_А1= 1,

Источник

Расчет простенка внутренней стены

Проверим прочность кирпичного простенка (толщиной 51 см, шириной 100 см, высотой 300 см) несущей ограждающей стены многоэтажного здания на действие эксплуатационных нагрузок (действующих на стадии эксплуатации здания). Толщина стен вышележащих этажей 38 см. Схема к расчету простенка представлена на Рис.1.

Исходные данные:

Ширина простенка: b=100 см;
Толщина стен вышележащих этажей: h₁=38 см;
Толщина рассчитываемого простенка: h₂=51 см;
Высота этажа (простенка): H=3 м

от стен вышележащих этажей: P₁=300 кН;
от веса перекрытия над рассматриваемым этажом: P₂=50 кН;
от веса стены рассматриваемого этажа (на участке а=45 см от низа перекрытия до верха простенка): P₃=6 кН.

Глубина заделки несущих конструкций перекрытия в стену c=20 см.
Расчетное сопротивление кладки сжатию R_сж=1 МПа (растяжение в кладке не допускается).

Рис.1. Схема к расчету кирпичного простенка

Подсчет нагрузок на простенок

Сила Р1 (см. Рис.1) приложена в центре тяжести сечения стены вышележащего этажа. Поскольку толщина стен рассматриваемого и вышележащего этажей неодинакова, эта сила приложена с эксцентриситетом e1 относительно центра тяжести стены рассматриваемого этажа и создает внешний момент, направленный против часовой стрелки (см. разрез 1-1):

Давление перекрытия на стену обычно принимают распределенным по закону треугольника (от максимума на грани стены до нуля в конце заделки). Следовательно, его равнодействующая P2 также имеет эксцентриситет e2 относительно центра тяжести сечения стены рассматриваемого этажа и вызывает момент противоположного направления, приложенный на уровне низа перекрытия:

Таким образом, на стену рассматриваемого этажа действует суммарная вышележащая сила от вышележащих конструкций:
и суммарный сосредоточенный момент, направленный против хода часовой стрелки:

Проверка прочности простенка

Полагаем, что кирпичная стена в пределах каждого этажа здания работает как вертикальная свободно лежащая на двух опорах (перекрытиях) балка пролетом H (см. Рис.1, б). Эпюры усилий показаны на Рис.1, в. Расчетным является сечение AB, расположенное на уровне верха простенка. В данном сечении возникает продольная сила сжатия:
и изгибающий момент, равный:

Площадь сечения простенка: F=b·h2=1·0.51=0.51 м 2 .

Момент сопротивления сечения:

Наибольшие напряжения сжатия возникают в ребре А. Проверим прочность простенка по формуле:

т.е. прочность простенка обеспечена.

Источник

Расчет простенка для каменных конструкций

1.1 Сбор нагрузок

Нагрузки на простенок:

Сбор нагрузок на простенок ведется в табличной форме .

Грузовая площадь: S = 2100 ∙ 2020 ∙ 10 -6 = 4,242 м 2 .

Таблица 1 – Нагрузки на простенок, передаваемые с покрытия

(δ = 5 мм, γ = 600 кг /м 3 )

(δ = 3 мм, γ = 600 кг /м 3 )

3. Paroc (плита Rob )

(δ = 20 мм, γ = 300 кг /м 3 )

4. Paroc (плита Ros )

(δ = 150 мм, γ = 200 кг /м 3 )

5. Полиэтиленовая пленка

(δ = 1 мм, γ = 600 кг /м 3 )

6. Paroc (плита Ros )

(δ = 60 мм, γ = 200 кг /м 3 )

7. Затирка цементно-песчаная

(δ = 10 мм, γ = 1800 кг /м 3 )

8. Разуклонка из керамзитобетона ( С 8/10 )

(δ = 20 мм, γ = 800 кг /м 3 )

9. Железобетонная плита

( b =1500 мм, l =6000 мм, h =220 мм, m =2720 кг)

10. Снеговая (г. Гомель, I Б р-он)

11. В том числе длительная

13.В том числе длительные

Таблица 2 – Нагрузки на простенок, передаваемые с перекрытия

1. Конструкция пола

2. Плита перекрытия

3. Стационарное оборудование

4. Вес людей и материалов

6.В том числе длительные

Удельные веса: — оконных проемов с окнами – 0,4 кН/м 2 ,

— каменной стены – 16,0 кН/м 3 (камни силикатные).

Таблица 3 – Нагрузки на простенок от веса окон и стены

Нормативное значение, кН

Коэффициент надёжности по нагрузке γ_f

Расчётная нагрузка, кН

1. Верхняя часть стены

2. Оконные проемы

3. Каменная стена

4. Нижняя часть стены

В итоге получаем:

— нагрузка от покрытия – 24,51 кН,

— нагрузка от перекрытия – 64,59 кН,

— нагрузка от верха стены – 4,31 кН,

— нагрузка от стены и окон – 41,35 кН,

— нагрузка от низа стены – 15,51 кН.

Расчетные нагрузки на простенок:

Расчет ведется в табличной форме

Таблица 4 – Расчетные нагрузки на простенок

Полная нагрузка, N (кН)

Нагрузки в уровне опирания ригеля на стену (верх ригеля)

Нагрузка в уровне верха оконного проема первого этажа

1.2 Расчет простенка на внецентренное сжатие

— расчетная нагрузка на простенок N = 346,64 кН,

— размеры простенка (таврового сечения): b ₁ = 900 мм, c = 120 мм,

— упругая характеристика кладки α = 1000 (табл. 15 СНиП),

— марка раствора М100, марка кирпича М250,

— расчетное сопротивление сжатию кладки R = 3,0 МПа (табл. 2 СНиП).

Рис. 1 – Простенок таврового сечения

Расчет выполняется по формуле:

, где

φ₁ – коэффициент продольного изгиба,

R – расчетное сопротивлении сжатию кладки,

A_c – площадь сжатой части сечения при прямоугольной эпюре напряжений,

, где

φ – коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента,

φ _c – коэффициент продольного изгиба для сжатой части сечения,

, где

l ₀ – расчетная высота (длина) элемента,

i_x – наименьший радиус инерции сечения элемента,

, где

i_xc –радиус инерции сжатой части поперечного сечения A_c в плоскости действиия изгибающего момента,

H – расстояние между перекрытиями или другими горизонтальными опорами (фактическая высота элемента).

Определение центра тяжести сечения простенка

A =( 120 ∙ 900 + 260 ∙ 770) ∙ 10 -2 = 3082,00 с м 2 ,

S = 770 ∙ 260 ∙ + 900 ∙ 120 ∙ ( + 260)) ∙ 10 -3 = 60586,00 см 3 ,

y = , где

S – статический момент инерции сечения,

A – площадь поперечного сечения,

y – расстояние от расчетной оси до центра тяжести сечения,

e ₀ – эксцентриситет расчетной силы N относительно центра тяжести сечения.

y = = 196,6 мм

Определение геометрических характеристик сечения простенка относительно центральной оси

Y_x – момент инерции всего сечения относительно главных осей,

Y_x ₁ – момент инерции «первой» части сечения,

Y_x ₂ – момент инерции «второй» части сечения,

Y_x ₁ =( + (196,6 — ) 2 ∙ 770 ∙ 260)∙ 10 -4 = 201579,24 см 4

Y_x ₂ = + (260 + 120 – 196,6 — ) 2 ∙ 900 ∙ 120)∙ 10 -4 = 177417,65 см 4

Y_x = 201579,24 + 177417,65= 378996,89 см 4

i_x =

i_x = = 11 ,09 м

= 25,97

По таблице 18 [СНиП] интерполяцией находим φ = 0,932.

Определение площади сжатой части сечения

= 94,1 мм

x – расстояние от точки приложения нагрузки N до крайней грани сжатого сечения,

h_c – высота сжатой части сечения.

A_c = 770∙ 154 , 1 ∙ 10 -2 =1186,57 см 2 .

Определение центра тяжести сжатой части сечения

y _с = , где

S_c – статический момент инерции сжатого сечения,

y_c – расстояние от расчетной оси до центра тяжести сжатого сечения,

e ₂ – расстояние от точки приложения нагрузки N до крайней грани сжатого сечения (в сторону действия момента).

S_c = 770 ∙ 154,1 ∙ ∙ 10 -3 = 9142,52 c м 3 ,

y_c = = 77,0 мм

Определение радиуса инерции сжатой части сечения

Y_x _с – момент инерции всего сжатого сечения относительно главных осей,

Y_x _с1 – момент инерции «первой» части сжатого сечения,

Y_x _с2 – момент инерции «второй» части сжатого сечения.

Y_xc ₁ = ∙ 10 -4 = 23481,04 см 4

Y_xc =23481,04+0,00=23481,04 см 4

i_x _с =

i_x _с = = 4,45 см

Проверка прочности простенка

= 71,91

По таблице 18 [СНиП] интерполяцией находим φ _c = 0,715.

= 0,824

По таблице 19 [СНиП] для сечения произвольной формы ω = 1 +

Условие 2 ∙ y h (по примечанию таблицы 19 [СНиП])

Условие не выполняется, следовательно 2 ∙ y = 2 ∙ y

ω = 1 + = 1,35

N_cc = 1,00 ∙ 0,824 ∙ 3,00 ∙1186,57∙1,35∙ 10 -1 = 395,98 кН

Условие выполняется, следовательно прочность простенка обеспечена.

Проверка необходимости расчета по раскрытию трещин

Проверка условия e ₀ > 0,7 ∙ y (по пункту 4.8 [СНиП])

Условие не выполняется, следовательно расчет по раскрытию трещин в швах кладки производить не нужно.

Источник