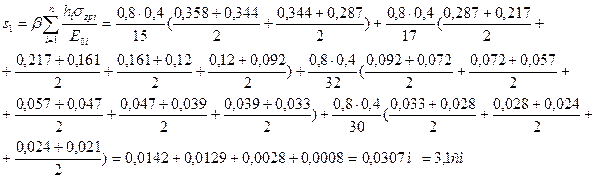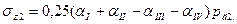- Пример расчета осадки при взаимном влиянии фундаментов.
- Промышленное строительство
- Материалы о строительстве промышленных объектов, зданий и сооружений
- 5.4.1. Определение давлении от влияния соседних фундаментов по методу угловых точек
- Учет влияния соседних загруженных площадей и фундаментов
- Страницы работы
- Содержание работы
Пример расчета осадки при взаимном влиянии фундаментов.



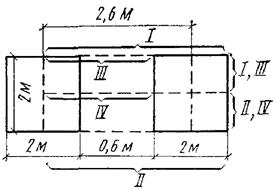
Определить методом элементарного суммирования осадку фундамента под колонну размером bXl=2X2 м глубиной заложения d=2,8 м, а также его дополнительную осадку в результате влияния соседнего фундамента, расположенного на этой же оси на расстоянии 2,6 м и имеющего такие же размеры и глубину заложения d=l,2 м. Среднее давление под подошвой первого фундамента pcp= 0,41 МПа, второго pcp=0,48 МПа. Грунтовые условия строительной площадки: 1 — песок пылеватый (γ1= 0,0185 МН/м 3 , h1 = 3,6 м, E1 = 15 МПа); 2 — супесь пластичная (γ2= 0,0195 МН/м 3 , h2 = 1,7 м; Е2=17 МПа); 3 — песок плотный (γ3=0,0101 МН/м 3 , h3 = 2,2 м, E3 = 32 МПа); 4 — суглинок тугопластичный (γ4 =0.01 МН/м 3 , h4=3,4 м, E4=30 МПа). Возводимое здание выполнено из железобетонного каркаса с заполнением.
Решение. Определим вертикальные напряжения от собственного веса грунта на уровне подошвы первого и второго фундаментов:
Ординаты эпюры природного напряжения и схема расположения фундаментов приведены на рис. 5.1. Дополнительные давления под подошвой первого и второго фундаментов равны:
pд1 = 0,41— 0,052 = 0,358 МПа; рд2 = 0,48—0,022 = 0,458 МПа.
Соотношение сторон фундаментов n=l/b=2/2=1. Чтобы избежать интерполирования по табл 1.16(Приложение I), зададимся значением m = 0,4, тогда высота элементарного слоя грунта hi = 0,4·2/2=0,4 м.
Проверим выполнение условия hi≤0,4b: 0,4 3 , h1 = 3,6 м, E1 = 15 МПа); 2 — супесь пластичная (γ2= 0,0195 МН/м 3 , h2 = 1,7 м; Е2=17 МПа); 3 — песок плотный (γ3=0,0101 МН/м 3 , h3 = 2,2 м, E3 = 32 МПа); 4 — суглинок тугопластичный (γ4 =0.01 МН/м 3 , h4=3,4 м, E4=30 МПа)
Построим эпюру дополнительного вертикального напряжения под подошвой первого фундамента (см. рис. V.1), воспользовавшись формулой σzp=αρдg и табл. 1.16(Приложение I). Вычисления представим в табличной форме (табл. V.1).
Нижнюю границу сжимаемой толщи находим по точке пересечения вспомогательной эпюры с эпюрой дополнительных напряжений (см. рис. V.1). По этому рисунку определим и мощность сжимаемой толщи H1=5,6 м.
Таблица V.1
| Грунт | z, м | m=2z/b | α | σz1= αρд1, МПа | Е, МПа |
| Песок пылеватый | 0,4 0,8 | 0,4 0,8 | 1,0 0,96 0,8 | 0,358 0,344 0,287 | |
| Супесь пластичная | 1,2 1,6 2,0 2,4 | 1,2 1,6 2,0 2,4 | 0,606 0,449 0,336 0,257 | 0,217 0,161 0,12 0,092 | |
| Песок плотный | 2,8 3,2 3,6 4,0 4,4 | 2,8 3,2 3,6 4,0 4,4 | 0,201 0,16 0,13 0,108 0,091 | 0,072 0,057 0,047 0,039 0,033 | |
| Суглинок тугопластичный | 4,8 5,2 5,6 * 6,0 6,4 6,8 7,2 7,6 | 4,8 5,2 5,6 6,0 6,4 6,8 7,2 7,6 | 0,077 0,066 0,058 0,051 0,046 0,04 0,036 0,032 | 0,028 0,024 0,021 0,018 0,016 0,014 0,013 0,011 |
Вычислим осадку фундамента без учета влияния соседнего фундамента:
По табл. 1.17(Приложение I) для здания, выполненного из железобетонного каркаса с заполнением, предельно допустимая осадка su=8 см. В нашем случае s1= 3,1
Рассчитаем осадку первого фундамента с учетом влияния рядом расположенного фундамента (см. рис. V.1). Для определения суммарных напряжений под центральной точкой первого фундамента воспользуемся методом угловых точек (рис. V.2). Для этого разобьем загруженную площадь на четыре прямоугольника I, II, III и IV (стороны прямоугольников показаны на рисунке фигурными скобками) и определим соотношения между сторонами каждого прямоугольника: nI = nII = 3,6/l =3,6; nIII = nIV = 1,6/1 =1,6.
Найдем дополнительное напряжение под центральной точкой первого фундамента от действия второго фундамента, предварительно вычислив соотношение m’= z/b = 1,6/2 = 0,8, где z — разность отметок глубины заложения первого и второго фундаментов (см. рис. V.1):
Из условий симметрии следует, что 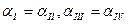
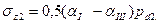
Коэффициент 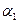
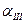
Рис. V.2
Дополнительные напряжения далее определим для точек, лежащих на вертикали под центральной точкой первого фундамента: эти напряжения вычисляли с шагом, равным высоте элементарного слоя, выбранного при расчете первого фундамента, т.е. z=0,4 м.
Вычисления представим в табличной форме (табл. V.2), при этом заметим, что предпоследний столбец этой таблицы характеризует распределение суммарных напряжений под центральной точкой первого фундамента от совместного действия первого и второго фундаментов.

Таблица V.2
| Грунт | z, м | m’=z/b | αI | αIII | σz2, МПа | Σσ=σz1+σz2, МПа | Е, МПа |
| Песок пылеватый | 1,6 2,0 2,4 | 0,8 1,2 | 0,880 0,816 0,751 | 0,859 0,781 0,703 | 0,005 0,008 0,011 | 0,363 0,352 0,298 | |
| Супесь пластичная | 2,8 3,2 3,6 4,0 | 1,4 1,6 1,8 2,0 | 0,692 0,633 0,584 0,535 | 0,631 0,558 0,500 0,441 | 0,014 0,017 0,019 0,022 | 0,231 0,178 0,139 0,114 | |
| Песок плотный | 4,4 4,8 5,2 5,6 6,0 | 2,2 2,4 2,6 2,8 3,0 | 0,500 0,456 0,424 0,392 0,366 | 0,397 0,352 0,318 0,284 0,258 | 0,024 0,024 0,024 0,025 0,025 | 0,096 0,081 0,071 0,064 0,058 | |
| Суглинок тугопластичный | 6,4 6,8 7,2 7,6 8,0 8,4 8,8 9,2 | 3,2 3,4 3,6 3,8 4,0 4,2 4,4 4,6 | 0,339 0,317 0,295 0,277 0,259 0,243 0,228 0,215 | 0,232 0,212 0,192 0,177 0,161 0,149 0,137 0,128 | 0,025 0,024 0,024 0,023 0,022 0,022 0,021 0,019 | 0,053 0,048 0,045 0,041 0,038 0,036 0,034 0,03 |
Пользуясь данными табл. V.2, построим суммарную эпюру дополнительных напряжений (см. рис. V.1). Нижнюю границу сжимаемой толщи найдем по точке пересечения этой эпюры со вспомогательной. Мощность сжимаемой толщи составит 7,6 м (см. рис. V.1).
Вычислим осадку первого фундамента, учитывая 
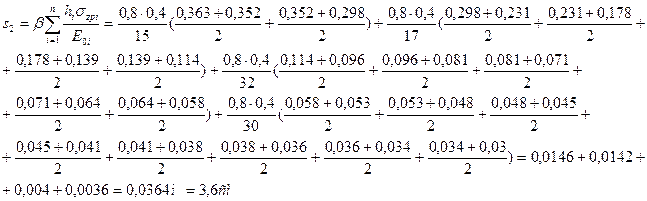
Источник
Промышленное строительство
Материалы о строительстве промышленных объектов, зданий и сооружений
5.4.1. Определение давлении от влияния соседних фундаментов по методу угловых точек
Осадки отдельных фундаментов рекомендуется определять с учетом влияния нагрузок от соседних фундаментов в тех случаях, когда соблюдается условие
Здесь:
Lф — расстояние между осями фундаментов в см;
Lr — расстояние (ординаты на графиках) в см, определяемое по графикам (рис. 5) в зависимости от ширины фундамента и давления р;
Кг — коэффициент, определяемый по формуле
, где b — ширина подошвы влияющего фундамента в см ;
Е — среднее значение модуля деформации в кг/см 2 .
Дополнительное давление от соседних фундаментов в центре рассматриваемого фундамента определяется с помощью метода угловых точек. По этому методу давление в угловой точке М прямоугольника АБВМ (рис. 6, а ) находится как четверть давления в центре учетверенного прямоугольника БГЕИ со сторонами 2 b1 и 2 l1 .
Давление в любой точке М прямоугольника АБВГ (рис. 6, б ) определяется как сумма угловых давлений от загрузки четырех прямоугольников I , II , III и IV .
Если точка М расположена вне контура прямоугольника АБДЕ (рис. 6, в ), то давление в этой точке будет равно алгебраической сумме угловых давлений от загрузки четырех прямоугольников ЖАВМ , ЖЕГМ , ИБВМ и ИДГМ , причем нагрузка первых двух берется со знаком плюс, а вторых — со знаком минус.
Величина давления в точке М на глубине z
где α — принимается по табл. 3 в зависимости от
b1 — меньшая сторона рассматриваемой части подошвы фундамента.
Дополнительная осадка от влияния соседних фундаментов определяется по формуле (5) или (7), причем значения pz подставляются в эти выражения из формулы (16).
Величина полной осадки получается путем суммирования основной осадки рассматриваемого фундамента и дополнительной осадки от влияния соседних фундаментов.
Рассмотрим возможные случаи расположения соседних фундаментов, взаимно влияющих на осадку.
Случай 1. Фундаменты расположены симметрично (рис.7). Давление в точке М от нагруженного фундамента АБВГ определяется по методу угловых точек как алгебраическая сумма угловых давлений от загрузки четырех прямоугольников: МаБг , МбВг , взятых со знаком плюс, и МаАв , МбГв — со знаком минус.
Случай 2. Фундаменты .расположены несимметрично (рис. 8). Давление в точке М от нагруженного фундамента АБВГ (рис. 8, а ) определится также как алгебраическая сумма угловых давлений от загрузки четырех прямоугольников: МаБг , МбВг , взятых со знаком плюс, и МаАв , МбГв — со знаком минус. При этом прямоугольники МаБг и МбВг , а также МаАв и МбГв не будут равны между собой, вследствие чего давление в точке М от их загрузки будет также разным.
Давление в точке М от нагруженного фундамента АБВГ (рис. 8, б ) равно алгебраической сумме угловых давлений четырех прямоугольников: МаБг , МбГв , взятых со знаком плюс, и МаАв , МбВг — со знаком минус.
Для всех случаев взаимного расположения соседних фундаментов угловое давление в точке М от загрузки любого прямоугольника, как указывалось выше, равно четверти давления в центре учетверенного прямоугольника со сторонами b1 , b2 и l1 , l2 (рис. 7 и 8). Так, например, угловое давление в точке М от загруженного прямоугольника МаБг (рис. 8, а ) со сторонами l1 /2 и b1 /2 равно четверти центрального давления от прямоугольника со сторонами l1 и b1, а угловое давление от прямоугольника МаАв (рис. 8, а ) со сторонами l2 /2 и b1 /2 равно четверти центрального давления от прямоугольного со сторонами l2 и b1 и т. д.
Методом угловых точек можно найти не только дополнительное давление и осадку от влияния соседних фундаментов, но и определить крен его, вызванный влиянием соседнего фундамента. Для этого необходимо найти осадку точки М , расположенной на контуре фундамента, крен которого определяется.
Источник
Учет влияния соседних загруженных площадей и фундаментов
Страницы работы
Содержание работы
1.5. Учет влияния соседних загруженных площадей и фундаментов
Учет влияния соседних загруженных площадей и фундаментов проводится на этапе определения осадки рассчитываемого фундамента (см. п. 1.1.5).
При определении осадки основания рассчитываемого фундамента с использованием расчетной схемы в виде линейно-деформируемого полупространства в первом приближении учитывается влияние всех соседних загруженных площадей и фундаментов, находящихся в пределах радиуса R = 1,2·Нс от вертикали, проходящей через центр подошвы рассчитываемого фундамента. Значение Нс принимают для рассчитываемого фундамента по условию σzp = 0,2·σzg (σzp = 0,1·σzg), в предположении, что соседние загруженных площади и фундаменты на значение σzp влияния не оказывают. Далее определяют дополнительные вертикальные напряжения σzp,nf на глубине z по вертикали, проходящей через центр рассчитываемого фундамента, с учетом влияния соседних фундаментов или нагрузок на прилегающие площади, попавших в пределы радиуса R = 1,2·Нс, по формуле:
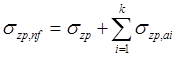
где: σzp – дополнительное вертикальное напряжение на глубине z под центром подошвы рассчитываемого фундамента; k – число влияющих фундаментов и площадей; σzp,ai – дополнительные вертикальные напряжения от влияющих фундаментов и площадей на глубине z под центром подошвы рассчитываемого фундамента, определяются методом угловых точек.
Далее определяют нижнюю границу сжимаемой толщи Нс‘ по условию σzp,nf = 0,2·σzg (σzp,nf = 0,1·σzg), разбивают сжимаемую толщу на элементарные слои грунта и определяют осадку рассчитываемого фундамента методом послойного суммирования, используя вместо значений σzp,i значения σzp,nf,i.
Во втором приближении дополнительно учитывается влияние всех соседних загруженных площадей и фундаментов, находящихся в пределах расстояния R’ = 1,2·Нс‘ от вертикали, проходящей через центр подошвы фундамента.
При определении осадки основания рассчитываемого фундамента с использованием метода эквивалентного слоя грунта (метода Цытовича) к значению основной осадки рассчитываемого фундамента, определенному в предположении, что соседние загруженных площади и фундаменты на значение осадки влияния не оказывают, добавляют значение дополнительной осадки от соседних загруженных площадей и фундаментов. Значение дополнительной осадки определяют последовательностью расчета, аналогичной методу угловых точек, только в данном случае определяется осадка точки, находящейся под углом загруженной площади.
Источник