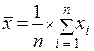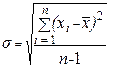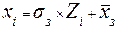Шкала стенов стандартное отклонение

Стен оценки — Sten scores

Результаты для некоторых шкал некоторых психометрических инструментов возвращаются в виде оценок sten, причем sten является аббревиатурой от «Standard Ten» и, таким образом, тесно связан с оценками stanine .

Содержание

Определение

Оценка sten указывает приблизительное положение человека (как диапазон значений) по отношению к совокупности ценностей и, следовательно, к другим людям в этой совокупности. Индивидуальные оценки стенограммы определяются со ссылкой на стандартное нормальное распределение. В отличие от оценок станина, у которых средняя точка равна пяти, у оценок стена нет средней точки (средней точкой является значение 5,5). Как и в случае со станнами, баллы по отдельным стенам разграничены половиной стандартного отклонения. Таким образом, оценка 5 по стандарту включает все стандартные оценки от -,5 до нуля с центром -0,25, а оценка по стандарту 4 включает все стандартные оценки от -1,0 до -0,5 и с центром в -0,75. Оценка 1 включает все стандартные оценки ниже -2,0. Стен 6-10 баллов, «зеркало» 5-1. В таблице ниже показаны стандартные баллы, определяющие стены, и процент людей, взятых из нормального распределения, которые получили бы баллы по стенам.

Стандартные / Z-баллы, проценты, процентили и оценки стен

Z-баллы	+2,0
Процентов	2,28%	4,41%	9,18%	14,99%	19,15%	19,15%	14,99%	9,18%	4,41%	2,28%
Процентиль	1.14	4,48	11,27	23,36	40,43	59,57	76,64	88,73	95,52	98,86
Стен	1	2	3	4	5	6	7	8	9	10

Процентили — это процентиль оценки sten (которая является средней точкой диапазона z-значений).

Баллы Sten (для всей совокупности результатов) имеют среднее значение 5,5 и стандартное отклонение 2.

Подсчет баллов стен

Когда распределение баллов приблизительно нормально распределено, баллы стен могут быть рассчитаны с помощью линейного преобразования: (1) баллы сначала стандартизируются; (2) затем умножается на желаемое стандартное отклонение 2; и, наконец, (3) добавляется желаемое среднее значение 5,5. Полученное десятичное значение можно использовать как есть или округлить до целого числа.

Например, предположим, что установлено, что баллы по шкале имеют среднее значение 23,5, стандартное отклонение 4,2 и приблизительно нормально распределены. Затем Стен баллов по этой шкале можно рассчитать по формуле, . Также обычно бывает необходимо усечь такие оценки, особенно если оценки искажены. ( s — 23,5 ) 4.2 2 + 5.5 <\ displaystyle <\ frac <(s-23.5)><4.2>> 2 + 5.5>

Альтернативный метод расчета требует, чтобы разработчик шкалы подготовил таблицу для преобразования исходных оценок в оценки стен путем распределения процентов в соответствии с распределением, показанным в таблице. Например, если разработчик шкалы замечает, что необработанные оценки 0–3 составляют 2% населения, то эти исходные оценки будут преобразованы в оценку sten, равную 1, а исходная оценка 4 (и, возможно, 5 и т. Д.) Будет преобразуется в оценку стенограммы, равную 2. Эта процедура представляет собой нелинейное преобразование, которое нормализует оценки стенокардии, и, как правило, получаемые в результате стены только приблизительно соответствуют процентным значениям, указанным в таблице. 16-факторный личностный опросник использует этот метод подсчета очков.

Источник

ПОРЯДОК ПЕРЕВОДА «СЫРЫХ» ПОКАЗАТЕЛЕЙ ПСИХОДИАГНОСТИЧЕСКИХ МЕТОДИК В СТАНДАРТНЫЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ (СТЕНЫ)

Исследование психических явлений требует многоаспектного анализа и применения разнообразного набора его конкретных методов в соответствии с поставленными задачами и общей стратегией проведения комплексной психодиагностики. При проведении мероприятий по профессиональному психологическому отбору и профессионально-психологическому сопровождению обучающийся обследуется с помощью целого комплекса методик, которые могут иметь совершенно различный интервал тестовых показателей. Полученные при сборе данных «сырые» (первичные) оценки далеко не всегда удобно использовать в дальнейшей работе. Особенно, когда возникает необходимость сравнить показатели испытуемого по разным методикам, получить интегральный показатель развития изучаемых качеств или отнести их к какой либо группе («успешных», «не успешных», «норме»). Для этого «сырые» оценки тем или иным способом преобразуют в значения стандартных тестовых шкал. Данные преобразования позволяют оценивать индивидуальный результат тестирования путем сопоставления его с тестовыми нормами (стандартной тестовой шкалой), полученными на выборке стандартизации. Выборка стандартизации специально формируется для разработки стандартной шкалы – она должна быть репрезентативна генеральной совокупности, для которой планируется применять данный тест, методику. Для получения нормального распределения величины измеряемого тестом свойства требуемое число испытуемых в ней обычно составляет не менее 200 человек. Впоследствии при тестировании предполагается, что и испытуемый, и выборка стандартизации принадлежат одной и той же генеральной совокупности. При стандартизации результатов тестовых испытаний чаще всего используется показатель среднеквадратичного отклонения – s. Стандартизация осуществляется при условии нормального распределения тестовых оценок в репрезентативной выборке испытуемых или близком к нему (рис. 1). Нормальным такое распре­деление называется потому, что оно очень часто встречалось в естественнонаучных исследованиях и казалось «нормой» всякого массового случайного проявления признаков. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции.

График нормального распределения может быть получен из полигона эмпирического распределения при бесконечном увеличении числа наблюдений и сужении интервалов до размеров точки. Он представляет собой куполообразную кривую, симметричную относительно центра группирования, имеющую строго определенные пропорции.

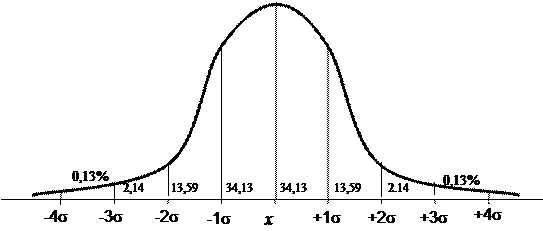Рисунок 1 – Нормальное распределение тестовых оценок в репрезентативной выборке испытуемых

Параметры распределения – это его числовые характеристики, указывающие, где «в среднем» располагаются значения признака, на­сколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака.

В реальных психофизиологических исследованиях оперируют не па­раметрами, а их приближенными значениями, так называемыми оценка­ми параметров.

Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой. Наибольшее практическое значение имеют:

— характеристики положения исследуемой совокупности (среднее арифметическое значение признака, медиана, мода);

— характеристики рассеяния (дисперсия);

— характеристики асимметрии (показатели асимметрии и эксцесса).

Среднее арифметическое (оценка математического ожидания) вы­числяется по формуле:

Символ S обозначает сумму всех значений xi, когда i принимает значения от 1 до n;

xi – общий член последовательности, подлежащий суммированию;

i – индекс суммирования, порядковый номер члена последовательности;

n – количество наблюдений.

Медианой (Ме) называется такое значение признака, когда одна половина значений экспериментальных данных меньше ее, а вторая больше.

Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто.

При нормальном распределении признака значения среднего арифметического, медианы и моды близки или совпадают друг с другом

Среднее квадратическое отклонение (s) — мера рассеяния вариант или оценка дисперсии — определяется по формуле:

где: xi – каждое наблюдаемое значение признака;

`x — среднее арифметическое значение признака;

n – количество наблюдений.

При нормальном распределении наибольшее отклонение крайней варианты от среднего арифметического составляет примерно 3s (правило «трех сигм»). Имеется определенное статистическое соответствие между отклонением признака от среднего арифметического и положением его в упорядоченном вариационном ряду. Кривая нормального распределения с процентным выражением распределений относительных частот в зависимости от величины отклонения от среднего арифметического представлена на рисунке

Одним из способов преобразования «сырых» результатов тестирования является нормирование. Суть нормирования состоит в переходе к другому масштабу — стандартным единицам измерения. Значимость стандартных шкал заключается, прежде всего, в том, что они позволяют отражать в одинаковых единицах измерения разнородные параметры, которые в обычных для этих параметров единицах измерения несопоставимы.

Простейшей из стандартных шкал является Z-шкала. Первичные значения показателя могут быть преобразованы в Z-оценки по формуле:

:

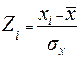
где: `x – среднее арифметическое показателя в выборке стандартизации;

xi – величина показателя теста в выборке стандартизации;

s – среднее квадратическое отклонение величин признака в выборке стандартизации.

Положительные значения Z-оценки соответствуют величинам выше среднего уровня, отрицательные значения — величинам ниже среднего. Единицей этой шкалы измерения является величина среднего квадратического отклонения. Среднее значение шкалы Z-оценок равно нулю.

Использование Z-оценок не всегда удобно, т.к. они могут принимать отрицательные и дробные значения. Поэтому часто Z-оценки преобразуют в другие шкалы, имеющие заданные среднее квадратическое отклонение и среднее значение. При этом используется формула:

где: `xз – заданное среднее значение шкалы;

sз – заданное среднее квадратическое отклонение.

Например, Р.Б. Кеттелл для стандартизации показателей методики 16-ФЛО предложил шкалу стенов – «стандартной десятки», где: 5,5 – заданное среднее значение показателя; 2 – заданное среднее квадратическое отклонение. Стенирование является одним из способов приведения нормированных оценок к виду, удобному для практического использования. Оно представляет собой перевод исходных тестовых оценок в выборке стандартизации в 10-балльную равноинтервальную шкалу (шкалу стенов). Практически это достигается путем разбиения оси значений тестовых оценок в выборке стандартизации на 10 интервалов, соответствующих долям среднеквадратичного отклонения s. При этом M (средняя арифметическая величина признака в выборке стандартизации) принимается за среднюю точку шкалы стенов. При этом всякое значение тестовых оценок, входящее в интервал от M до M + 0,5s, приравнивается к 6 баллам по шкале стенов, а, входящее в интервал от M до M – 0,5s, – к 5 баллам этой шкалы. Такая же процедура с шагом увеличения равным 0,5s проводится для вычисления 7, 8, 9 и 10 баллов стеновой шкалы и с шагом уменьшения на 0,5 s – для вычисления 4, 3, 2, и 1 балла шкалы стенов (рис.1).

1 стен = М – 2,5 σ 2 стена = М – 2 σ 3 стена = М – 1,5 σ 4 стена = М – 1 σ 5 стенов = М – 0,5 σ

6 стенов = М +0,5 σ 7 стенов = М + σ 8 стенов = М +1,5 σ 9 стенов = М +2 σ 10 стенов = М +2,5 σ

Получение 10 балльного ряда и есть шкала перевода «сырых» оценок в стены. При такой системе стандартизации диапазон, который принято называть средним или нормой (диапазон в 1s), характеризуется стандартными единицами от 4 до 7 стенов. Стандартные оценки от 3 или 8 стенов свидетельствуют об индивидуальных различиях, выходящих за границы средней нормы. Оценки в 2 и 9 стенов получаются при значительном отклонении индивидуальных оценок, на 2s выше и ниже среднего группового значения. Максимальная оценка в 10 стенов достигается при отклонении индивидуального тестового результата на 2,5s и более, вверх от средней нормы. Аналогичным образом, оценка в 1 стен ставится за все отклонения индивидуального тестового результата от среднего значения на 2,5s и ниже.

Для перевода «сырых» оценок в стены можно также использовать формулу линейного преобразования шкалы Z – оценок ( 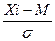) нормального распределения в десятибальную шкалу стенов:

St = 2 × ( 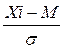)+ 5,5,

где Xi – значение признака (в «сырых» баллах); M – среднее арифметическое значение признака; σ – среднеквадратичное отклонение значений признака.

При отклонении распределения значений признака (оценок в «сырых» баллах) от их нормального распределения используют процентильную шкалу перевода оценок в стены. Процентиль (X%) – это такое значение «сырой» оценки, которое соответствует частоте оценок меньших и равных по значению данной «сырой» оценке в %.

Перевод значения «сырой» оценки, выраженной в процентилях, в стены осуществляется по стандартной шкале (рисунок 1, таблица 2), где значения оценок в стенах связаны с величинами частот.

Для каждого теста по результатам тестирования стандартизованной выборки с использованием шкалы перевода процентилей в стены определяют границы стеновых оценок в значениях «сырых» оценок и строят шкалу перевода «сырых» оценок теста в стены (рисунок 1, таблица 2),.

Границы стеновых оценок в значениях «сырых» оценок определяют по граничным значениям частотных интервалов, указанных в таблице 1 для каждой стеновой оценки.

Например, по результатам обследования результат испытуемого входит в диапазон «сырых» оценок (X5) стандартизованной выборки, что соответствует частоте оценок в % (процентиль) [30,86; 50,0] и, соответственно, 5 стенам.

Таблица 1. Перевод процентильной шкалы в стены

Стены
Частота оценок (%)
Диапазон «сырых» оценок в стандартной выборке	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10

При создании стеновой шкалы следует учитывать конструктивные особенности теста. Возможно создание стеновой шкалы на основе обратно пропорциональной зависимости, когда более высокий «сырой» балл свидетельствует о меньшей степени выраженности изучаемой характеристики, например, такая шкала применяется в тесте «Адаптивность».

Источник