Знатоки физики или кто сможет, помогите.
Я очень хочу решить задачу, но у меня не получается:
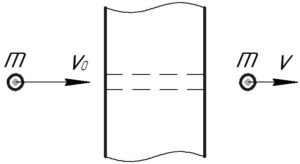
Свинцовая пуля пробивает деревянную стенку, причем скорость в момент удара о стенку была v = 400 м/с, а в момент вылета v1 = 100 м/с. Какая часть пули расплавилась, считая, что на нагревание ее идет 60% потерянной механической энергии? Температура пули в момент удара t1 = 50° С. Удельная теплоемкость свинца с = 125,7 Дж/(кг К) , температура плавления tп = 327°С, удельная теплота плавления λ = 26,4•103 Дж/кг.
В ответе Валерия Яновича есть непринципиальные неточности (несоответствие индексов) , и одна принципиальная ошибка.
Правильный ответ будет такой: 0,6*M*(v^2 — v1^2)/2 = M*c*(tп — t1) + m*л.
Поясняю: Кинетическая энергия пули перед моментом удара была E1=M*v^2/2, где М — масса ВСЕЙ пули.
Кинетическая энергия пули после прохождения через доску: Е2=M*v1^2/2.
Пуля потеряла кинетическую энергию (Е1-Е2)=M*v^2/2-M*v1^2/2=М*(v^2-v1^2)/2.
Эта разность кинетических энергий преобразовалась в тепло Q1, пошедшее на нагрев и частичное расплавление пули, в работу А по разрушению части доски, и тепло Q2, пошедшее на нагрев части доски.
Q1=0,6* (Е1-Е2)=0,6*M*(v^2-v1^2)/2.
Часть этого тепла Q3 затратилась на нагрев ВСЕЙ пули (а не только расплавившейся части, как посчитал Валерий Янович) до температуры плавления: Q3=M*c*(tп — t1). Оставшаяся часть Q4=Q1-Q3=m*л — пошла на расплавление части пули. Масса расплавившейся части пули равна m. Символом «л» Валерий Янович обозначил удельную теплоту плавления свинца.
После подстановки всех значений и получается: 0,6*M*(v^2 — v1^2)/2 = M*c*(tп — t1) + m*л,
или, если сохранить заданные обозначения, 0,6*M*(v^2 — v1^2)/2 = M*c*(tп — t1) + m* λ.
Отсюда получаем: m/M=(0,3*(v^2 — v1^2)-c*(tп — t1))/ λ.
Очень просто. 0,6M(v^2 — vo^2)/2 = m(c(t1 — t2) + л) Отсюда найди отношение m/M
Источник
Свинцовая пуля пробивает доску, при этом её скорость падает с 400 до 200 м/с
Условие задачи:
Свинцовая пуля пробивает доску, при этом её скорость падает с 400 до 200 м/с. Какая часть пули расплавится? Нагреванием доски пренебречь. Начальная температура пули 27 °C.
Задача №5.3.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
\(\upsilon_0=400\) м/с, \(\upsilon=200\) м/с, \(t_0=27^\circ\) C, \(\alpha-?\)
Решение задачи:
Согласно закону сохранения энергии, количество теплоты \(Q\), выделившееся при пробивании доски пулей, равно изменению кинетической энергии пули, поэтому верно записать:
Пусть \(m\) – полная масса пули, а \(\Delta m\) – масса расплавившейся части пули. Величину \(\alpha\) тогда следует искать по формуле:
Чтобы расплавить часть пули массой \(\Delta m\), необходимо сначала всю пулю массой \(m\) нагреть до температуры плавления (\(t_п=327^\circ\) C). Учитывая, что нагреванием доски можно пренебречь, количество теплоты \(Q\) также можно выразить следующим образом:
\[Q = cm\left( <
Удельная теплоёмкость свинца \(c\) равна 130 Дж/(кг·°C), удельная теплота плавления свинца \(\lambda\) равна 25 кДж/кг.
Приравняем (1) и (3), тогда получим:
Теперь поделим обе части уравнения на массу пули \(m\):
Учитывая, что \(\alpha = \frac<<\Delta m>>
Осталось только выразить величину \(\alpha\):
Ответ: 0,84.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Свинцовая пуля, летящая со скоростью 430 м/с, пробивает стену, причем скорость
Условие задачи:
Свинцовая пуля, летящая со скоростью 430 м/с, пробивает стену, причем скорость её уменьшается до 200 м/с. Какая часть пули при этом расплавится? Начальная температура пули 50 °C, на нагревание пули затрачивается 50% потерянной кинетической энергии.
Задача №5.3.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
\(\upsilon_0=430\) м/с, \(\upsilon=200\) м/с, \(t_0=50^\circ\) C, \(\alpha=50\%\), \(\beta-?\)
Решение задачи:
Пусть \(m\) – масса пули, а \(\Delta m\) – масса части пули, расплавившейся при пробивании стены. Тогда искомую величину \(\beta\), очевидно, будем находить по формуле:
Выделившееся при прохождении пули сквозь стену количество теплоты \(Q\) равно изменению кинетической энергии пули (по закону сохранения энергии), поэтому:
В условии говорится, что на нагревание пули затрачивается лишь \(\alpha\) часть потерянной кинетической энергии (другая часть, вероятно, “нагревает” стену), поэтому справедливо:
Чтобы часть пули расплавилась, она обязательно должна нагреться до температуры плавления (\(t_п=327^\circ\) C). Количество теплоты \(Q_1\) необходимо искать по формуле:
Здесь \(c\) – удельная теплоёмкость свинца, равная 130 Дж/(кг·°C), \(\lambda\) – удельная теплота плавления свинца, равная 25 кДж/кг.
Приравняем (3) и (4), тогда получим:
\[\alpha Q = cm\left( <
Также, учитывая (2), это уравнение примет вид:
Обе части поделим на величину \(m\):
Учитывая формулу (1), имеем:
В итоге, решение задачи в общем виде следующее:
Подставив все величины в последнюю формулу (величину \(\alpha\) подставляем в долях единицы), посчитаем ответ:
Ответ: 0,86%.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если не сложно,можете написать,как предложил Вова
Давайте попробуем.\[\alpha \left( <\frac<
А почему б не так написать закон изменения кинетической энергии пули:
Q = mv20 /2 – (m – Δm) v2 / 2 ?
Ведь масса пули на выходе становится меньше на Δm.
Вы хотите сказать, что расплавленная часть пули осталась в стене?
Даже не задумывался об этом, если честно. По логике Вы рассуждаете верно.
Но Ваша задача станет более громоздкой в решении, а ответ будет примерно тем же самым, можете в этом самолично убедиться 
Источник
Олимпиада по физике
Олимпиада по физике
1. С одинаковой высоты упали два одинаковых по массе тела — медное и железное. Какое из них при падении нагрелось до более высокой температуры?
2. Супермен стоит в окне на высоте 30 м над улицей. Мимо пролетает ребёнок, которого выронили из окна, находящегося на 15 м выше. С каким постоянным ускорением должен супермен спускаться по лестнице ( из состояния покоя ), чтобы успеть поймать падающего ребёнка?
3. Жук-плавунец может находится в воде без движения. Попав в ручей, жук может двигаться против течения с максимальной скоростью v1, а по течению — с максимальной скоростью v2. С какой максимальной скоростью может двигаться жук перпендикулярно течению ручья?
4. Одинаковые резисторы включены A
в сеть так, как показано на рисунке.
Какой из резисторов потребляет
5. В каком случае процесс теплообмена произойдёт быстрее, если в горячую воду наливать холодную, или, если в холодную наливать горячую то же массы?
1. Модели корабля толчком сообщили скорость v0 = 10 м/с. При движении модели на неё действует сила сопротивления, пропорциональная скорости: F = kv. Найдите путь пройденный моделью за время, в течении которого её скорость уменьшилась до нуля. Считать k= 0,5 кг/с, массу m= 0,5 кг.
2. В каком случае процесс теплообмена произойдёт быстрее, если в горячую воду наливать холодную, или, если в холодную наливать горячую то же массы?
3. Свинцовая пуля пробивает деревянную стенку, причём скорость удара о стенку была 400 м/с, а в момент вылета 100 м/с. Какая часть пули расплавилась, считая, что на нагревание её идёт 60% потерянной механической энергии? Температура пули в момент удара 50°С. Теплоёмкость свинца 125,7 Дж/кг°С, температура плавления 327°С, удельная теплота плавления 26,4 ×103 Дж/ кг
4. Подставку, на которой лежит тело подвешенное на пружине,
начинают опускать с ускорением а. В начальный момент
пружина не растянута. Через какое время тело оторвётся от
подставки? Масса тела М, жесткость пружины k.
5. Сосуд наполовину заполнен водой, в которой плавает кусок льда. Поверх льда наливают керосин, верхний уровень которого устанавливается на высоте h от дна сосуда. Как измениться эта высота, когда лёд растает?
1. Кубик льда плотности 0,92×103 кг/м3 плавает в стакане с водой. Какая часть его объёма выступает из воды? Что произойдёт с уровнем воды в стакане, когда лёд растает?
2. Подвешенный на нити шарик массой m совершает колебания в вертикальной плоскости. Когда шарик проходит положение равновесия, сила натяжения нити T1 = 2mg. На какой максимальный угол a отклонится шарик? Чему равна сила Т2 натяжения нити в момент наибольшего отклонения шарика?
3. Коротко замкнутая катушка, состоящая из N = 1000 витков проволоки, помещена в магнитное поле, направленное вдоль оси катушки. Площадь поперечного сечения катушки S = 40 см2, её полное сопротивление R = 160 Ом. Найти количество тепловых потерь в катушке, если индукция магнитного поля равномерно изменяется со скоростью 10-3 Тл/с.
4. Что нужно делать для приёма более коротких волн — увеличивать или уменьшать площадь перекрытия в конденсаторе переменной ёмкости?
5. На сколько равных частей надо разрезать проводник сопротивлением 25 Ом, что бы при параллельном соединении этих частей получить сопротивление в 25 раз меньшее?
1. Железное и деревянное тело равных масс бросили в воду. Одинаковые ли выталкивающие силы действуют на эти тела?
2. Какое время понадобиться, что бы на катере пройти расстояние 1,5 км туда и обратно по реке, скорость течения которой 2 км/ч? Скорость катера относительно воды 8 км/ч.
3. Атмосферное давление уменьшается при подъёме на гору. Какой из приведённых факторов является основной причиной этого явления: а) Уменьшается высота воздушного столба; б) Уменьшается плотность воздуха в) Уменьшается сила притяжения Земли; г) Меняется состав воздуха?
4. Три кирпича поставлены так как
показано на рисунке:
Одинаковые ли силы, действующие на опору и давление в обоих случаях?
1. Если стальной шарик, проходящий сквозь стальное кольцо, нагреть, то он застрянет в кольце (рис). Что произойдет, если нагреть не шарик, а кольцо?
Что произойдет, если нагреть до одинаковой температуры шарик и кольцо?
2. Что тяжелее 1 л дистиллированной воды при 20°С или 1 л питьевой воды при той же температуре?
3. Что общего между склеиванием деревянных изделий, сваркой металлов и паянием их? Объяснить на основе знании й о молекулах и их движении.
Если теплоёмкость одного тела больше, чем теплоёмкость другого, то при нагревании первое тело нагреется за одно и то же время до меньшей температуры, следовательно, так как теплоёмкость железа больше, чем теплоёмкость меди, то оно нагреется меньше, чем медь
Дано Р е ш е н и е:
h= 30 м Что бы супермен поймал ребёнка t1= t2,
Dh = 15 м где t1 — время движения ребёнка с высоты h,
t2 — 
время движения супермена. Найдём время
а — ? движения ребёнка до положения супермена из
формулы Dh =gt02 / 2, т. е. 
.
Всё время падения ребёнка будет 
. Время
движения супермена t2 = t1- t0 , путь супермена h = at22/ 2,
отсюда а = 2h / t22 = 2h / (t1- t0 )2. t = 3 c t0 = 1,73 c t2 = 1,27 c
v1 = vж — vт vж = v1 + vт,
v2 = vж + vт, v2 = v1 + 2vт.
vж vот vот = Ö( vж2 — vт2 ) см. рисунок
vт vж = (v2 + v1 )/ 2 тогда
Дано: Р е ш е н и е:
R1 = R2 Потребляемая энергия пропорциональна току
A = Jut. Напряжение и время у резисторов
A — ? одинаковое. Но в цепи первого резистора стоит
амперметр, следовательно, сопротивление этой ветви больше, а ток в ней меньше, значит J2 > J1, поэтому второй резистор потребляет больше энергии, чем первый.
Когда горячую воду льём в холодную, т. к. горячая вода вначале попадает вниз, а затем начнёт подниматься кверху, отдавая своё тепло. Холодная же вода подниматься кверху не будет, она останется на дне, поэтому теплообмен будет происходить медленнее.
v1 = 0 v02 — v12 = 2aS S = v02 / 2a
По закону Ньютона
ma = Fc amax = kv0/m aср = kv0/2m, тогда S = 10 м
Когда горячую воду льём в холодную, т. к. горячая вода вначале попадает вниз, а затем начнёт подниматься кверху, отдавая своё тепло. Холодная же вода подниматься кверху не будет, она останется на дне, поэтому теплообмен будет происходить медленнее.
Дано Р е ш е н и е:
v0 = 400 м/с По закону сохранения энергии
v = 100 м/с m1v02/2 = m2v2/2 + Еп отсюда
Q = 0,6 Еп Еп = m1v02/2 — m2v2/2
t = 50°C Q = 0,6(m1v02/2 — m2v2/2
c = 125,7 Дж/(кг°C) Q = Q1 + Q2 Q1 — теплота нагрева
t2 = 327°C пули Q1 = cm1Dt
l = 26,4×103 Дж/кг Q2 — теплота, пошедшая на плавление
части пули Q2 = lm2
m2/m1 — ? Q = cm1Dt + lmРешим
совместно ( 1 ) и ( 2 )
0,6m1v02/2 — 0,6m2v2/2 = cm1Dt + lm2 поделим обе части
равенства на m1 0,6v02 — 0,6v2m2/m1 = 2cDt + 2lm2/m1
m2/m1( 2l + 0,6 v2 ) = 0,6v02 — 2сDt
m2/m1= ( 0,6v02 — 2сDt )/ ( 2l + 0,6 v2 )
m2/m1= 0,47 т. е. m2 составляет от m1 47%
Решение:
0 По второму закону Ньютона
a Fу 0Х: mg — Fу — N = ma
N В момент отрыва N = 0, т. е.
mg — Fу = ma Fу =kDx
mg Dx = m(g — a)/ k из формулы Dx = at2/ 2
x t = Ö 2Dx/a =Ö 2 m(g — a)/ ak
Сосуд с влажным воздухом легче. В равных объёмах газов
при одинаковых давлениях содержится одинаковое число
молекул. Значит во влажном воздухе молекулы вода просто
заменили такое же количество молекул воздуха. Но молярная
масса воздуха больше молярной массы воды. Поэтому сосуд
с сухим воздухом тяжелее чем с влажным.
Дано Р е ш е н и е:
rл = 920 кг/м3 FA По условию равновесия
rв = 1000 кг/м3 FA= mg FA=rв g V1,
где V1- часть, погружённая
DV/V — ? mg в воду. FA=rв g ( V — DV )
rв gV — rв g DV = rл g V
DV/V= (rв — rл )/rв » 0,08
Если лёд растает уровень воды в стакане не понизится.
Дано Р е ш е н и е:
Т1 = 2mg В положении 1
Y 0Y: ma = T1 — mg
T2 — ? Y a T2 a = v2/ R R = l — длина нити
a — ? T1 mv2/ l = mg v2=lg
h 2 0 cos a = ( l — h ) / l
1 По закону сохранения энергии
0 mg mv2/ 2 = mgh h = v2/ 2g = l/2
mg cos a = 1/2 a = 60°
В положении 2 ось 0Y направим вдоль нити, тогда а = 0, имеем
T2 — mg cos a = 0 T2 = mg cos a = mg / 2
Дано Р е ш е н и е:
S = 40 см2 Q = U2t / R U = Ei
R = 160 Ом Ei = — DФ/Dt = — SNDВ/Dt = — 4×10-4 ( В )
DВ/Dt = 10-3 Тл/с Q = 10-9 Дж
Q — ?
Из формулы Томсона и соотношения l = сТ следует, что
, где с — скорость света. Следовательно ёмкость конденсатора надо уменьшать. По формуле ёмкости С =ee0S/d следует, что для уменьшения ёмкости площадь перекрытия надо уменьшать.
Дано Р е ш е н и е:
R = 25 Ом Т. к. частей равное количество
R¢ = 1 Ом R1= R2 = . = R / n = R0
n — ? По закону параллельного соединения
проводников 
т. е. 
Источник