- Библиотека: книги по архитектуре и строительству | Totalarch
- Вы здесь
- Таблицы для определения осадок фундаментов. Юрик Я.В. 1971
- Предисловие
- 5.5.4. Расчет деформаций основания (ч. 1)
- А. ОСАДКИ ФУНДАМЕНТОВ
- ТАБЛИЦА 5.17. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА kc
- ТАБЛИЦА 5.18. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА km
- ТАБЛИЦА 5.19. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА k
- ТАБЛИЦА 5.20. ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ k0, k1, k2, k3
- ТАБЛИЦА 5.21. ЗНАЧЕНИЕ КОЭФФИЦИЕНТА kr
- ТАБЛИЦА 5.22. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА ω
Библиотека: книги по архитектуре и строительству | Totalarch
Вы здесь
Таблицы для определения осадок фундаментов. Юрик Я.В. 1971
| Таблицы для определения осадок фундаментов (Пособие для расчета оснований по деформациям) |
| Юрик Я.В. |
| Издательство «Будiвельник». Киев. 1971 |
| 196 страниц |
В книге помещены таблицы для определения осадок фундаментов на однородных (однослойных) и неоднородных (многослойных) основаниях. Таблицы составлены для фундаментов разных форм, размеров и глубин заложения, в том числе для свайных и плитных фундаментов, при различных удельных давлениях на основание. Приводятся примеры, иллюстрирующие практическое применение таблиц. Книга рассчитана на инженерно-технических работников проектных и строительных организаций.
Определение осадок фундаментов на однородных (однослойных) основаниях
Определение осадок фундаментов на неоднородных (многослойных) основаниях
Общие принципы и порядок расчета осадок фундаментов методом послойного суммирования
Особенности расчета осадок свайных фундаментов
Методика разработки таблиц для определения осадок фундаментов
Ленточные фундаменты
Квадратные столбовые и свайные фундаменты
Прямоугольные столбовые и свайные фундаменты
Прямоугольные столбовые фундаменты
Квадратные плитные фундаменты
Прямоугольные плитные фундаменты
Круглые фундаменты
Предисловие
В соответствии со строительными нормами и правилами, введенными в 1962 г., расчет оснований зданий и сооружений производится по предельным состояниям.
Метод расчета оснований по предельным состояниям, разработанный советскими учеными, является более прогрессивным по сравнению с принятыми ранее методами расчета по допускаемым давлениям и расчетным сопротивлениям, не учитывающими взаимодействия сооружений с их основаниями.
Задачей расчета оснований по деформациям является ограничение деформаций надфундаментных конструкций, происходящих в результате осадки грунтов, такими пределами, которые гарантируют от появления недопустимых для нормальной эксплуатации конструкций трещин и повреждений, а также от изменения проектных уровней и положений.
С введением расчета по предельным состояниям значительно повысились требования к проектированию оснований. В частности, расчет оснований по деформациям стал обязательным для всех проектируемых зданий и сооружений, фундаменты которых опираются на нескальные грунты.
Наиболее трудоемкой частью расчета оснований по деформациям является расчет осадок отдельных фундаментов.
Расчет осадок фундаментов, который производится методом послойного суммирования по формулам СНиП П-Б. 1—62*, связан с большим объемом вычислительных работ. Трудоемкость расчета усугубляется еще и тем, что в процессе проектирования возникает необходимость в многократном повторении расчетных операций.
С целью максимального сокращения затрат времени на вычисление величин осадок отдельных фундаментов разработаны помещенные в настоящей книге таблицы.
В таблицах содержатся величины полных осадок фундаментов на однородном (однослойном) основании и осадок отдельных слоев основания разной толщины, вычисленные по соответствующим формулам СНиП II-Б. 1—62* в зависимости от возможных значений удельного давления на основание, глубины заложения и размеров подошвы фундаментов различных зданий и сооружений.
По значениям осадок отдельных слоев основания легко определить величины полных осадок фундаментов на неоднородных (многослойных) основаниях.
В последние годы резко увеличился объем строительства многоэтажных, массивных и высотных промышленных и гражданских зданий и сооружений. Наряду с этим часто застраиваются площадки со сложными грунтовыми условиями, в том числе участки, сложенные на значительную глубину слабыми грунтами.
В этих условиях начали широко применять свайные фундаменты, а также сплошные фундаментные плиты на естественном основании с большими размерами в плане (плитные фундаменты).
В связи с широким применением свайных и плитных фундаментов появилась необходимость переработки книги. Последняя дополнена таблицами для определения осадок прямоугольных плитных фундаментов шириной 12,0 — 24,0 м. Таблицы величин осадок квадратных фундаментов и прямоугольных фундаментов с отношением сторон l : b = 1,2 : 2,0 переработаны с учетом приспособления их для определения осадок свайных фундаментов (свайных кустов) при погружении свай на глубину до 16,0 м от природного рельефа.
Автор приносит глубокую благодарность всем лицам, приславшим критические замечания по первому изданию. Последние были учтены при подготовке настоящего издания.
Источник
5.5.4. Расчет деформаций основания (ч. 1)
А. ОСАДКИ ФУНДАМЕНТОВ
Определение осадки методом послойного суммирования. В методе послойного суммирования приняты следующие допущения:
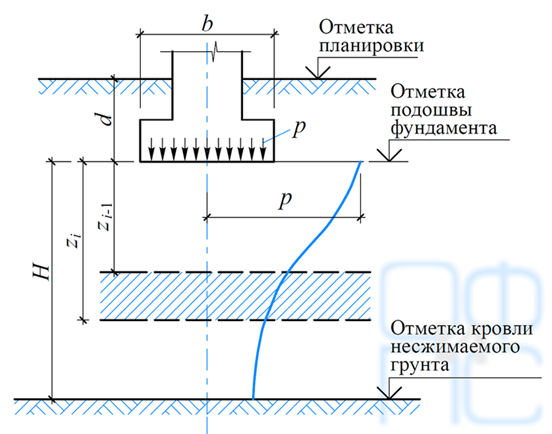
- – осадка основания вызывается дополнительным давлением р0 , равным полному давлению под подошвой фундамента р за вычетом вертикального нормального напряжения от собственного веса грунта на уровне подошвы фундамента: р0 = р – σzg,0 (при планировке срезкой принимается σzg,0 = γ´d , при отсутствии планировки и планировке подсыпкой σzg,0 = γ´dn , где γ´ — удельный вес грунта, расположенного выше подошвы; d и dn — глубина заложения фундамента от уровня планировки и природного рельефа);
- – распределение по глубине дополнительных вертикальных нормальных напряжений σzp от внешнего давления р0 принимается по теории линейно-деформируемой среды как в однородном основании (см. п. 5.2);
- – при подсчете осадок основание делится на «элементарные» слои, сжатие которых определяется от дополнительного вертикального нормального напряжения σzp , действующего по оси фундамента в середине рассматриваемого слоя;
- – сжимаемая толща основания ограничивается глубиной z = Нс , где выполняется условие
Если найденная по условию (5.59) нижняя граница сжимаемой толщи находится в слое грунта с модулем деформации Е z = Hc , нижняя граница сжимаемой толщи определяется исходя из условия σzp = 0,1σzg .
Осадка основания s методом послойного суммирования определяется по формуле
где β — безразмерный коэффициент, равный 0,8; σzp,i — среднее значение дополнительного вертикального нормального напряжения в i -м слое грунта, равное полусумме указанных напряжений на верхней zi-1 и нижней zi границах слоя по вертикали, проходящей через центр подошвы фундамента; hi и Еi — соответственно толщина и модуль деформации i -го слоя грунта; n — число слоев, на которое разбита сжимаемая толща основания.
При этом распределение вертикальных нормальных напряжений по глубине основания принимается в соответствии со схемой, приведенной на рис. 5.26.
Дополнительные вертикальные нормальные напряжения по вертикали, проходящей через центр рассматриваемого фундамента, на глубине z от его подошвы определяются:
σzp — от дополнительного давления р0 под подошвой рассчитываемого фундамента [см. формулу (5.12)]; σzp,A — от дополнительного давления р0j под подошвой j -го влияющего фундамента методом угловых точек по формуле (5.18).
Суммарное дополнительное напряжение по оси рассчитываемого фундамента с учетом влияния нагрузок от соседних фундаментов определяется по формуле (5.19).
Пример 5.12. Рассчитать осадку фундамента Ф-1 здания с гибкой конструктивной схемой с учетом влияния нагрузки на фундамент Ф-2 по условиям примера 5.2 (см. рис. 5.11) при следующих данных. С поверхности до глубины h + h1 = 6 м залегает песок пылеватый со следующими характеристиками, принятыми по справочным таблицам (см. гл. 1): γs = 26,6 кН/м 3 ; γ = 17,8 кН/м 3 ; ω = 0,14; е = 0,67; сII = 4 кПа; φII = 30°; E = 18 000 кПа. Ниже залегает песок мелкий с характеристиками: γs = 26,6 кН/м 3 ; γ = 19,9 кН/м 3 ; ω = 0,21; е = 0,62; сII = 2 кПа; φII = 32°; E = 28 000 кПа. Уровень подземных вод находится на глубине 6,8 м от поверхности. Суммарная нагрузка на основание от каждого фундамента (с учетом его веса) N = 5,4 МН.
Решение. По формуле (5.21) удельный вес песка мелкого с учетом взвешивающего действия воды
γsb = (26,6 – 10)/(1 + 0,62) = 10,2 кН/м 3 .
По табл. 5.11 находим: γc1 = 1,2 и γc2 = 1. По табл. 5.12 при φII = 30° находим: Mγ = 1,15; Мq = 5,59; Мc = 7,95. Поскольку характеристики грунта приняты по таблицам, k = 1,1.
По формуле (5.29) получаем:

Среднее давление под подошвой
р = 5400/4 2 = 338 кПа R = 341 кПа;
дополнительное давление на основание
Дополнительные вертикальные нормальные напряжения в основании фундаментов Ф-1 и Ф-2 подсчитаны в примере 5.2, приведены в табл. 5.6 и показаны на рис. 5.11. Дополняем табл. 5.6 подсчетом напряжений от собственного веса грунтов σzg для определения нижней границы сжимаемой толщи (табл. 5.16).
Из табл. 5.16 видно, что нижняя граница сжимаемой толщи под фундаментом Ф-1 находится на глубине z1 = 8,0 м (при учете нагрузки только на этот фундамент) и на глубине z2 = 8,8 м (при учете влияния фундамента Ф-2).
ТАБЛИЦА 5.16. К ПРИМЕРУ 5.12
| z , м | σzp1 | σzp2 | σzp | σzg | 0,2 σzg | E |
| 0 | 300 | 0 | 300 | 36 | 7 | 18 000 |
| 0,8 | 288 | 0 | 288 | 50 | 10 | |
| 1,6 | 240 | 0 | 240 | 64 | 13 | |
| 2,4 | 182 | 1 | 183 | 78 | 16 | |
| 3,2 | 135 | 2 | 137 | 93 | 19 | |
| 4,0 | 101 | 3 | 104 | 107 | 21 | |
| 4,8 | 77 | 4 | 81 | 123 | 25 | 28 000 |
| 5,6 | 60 | 5 | 65 | 131 | 26 | |
| 6,4 | 48 | 6 | 54 | 139 | 28 | |
| 7,2 | 39 | 6 | 45 | 147 | 29 | |
| 8,0 | 32 | 7 | 39 | 156 | 31 | |
| 8,8 | 27 | 7 | 34 | 164 | 33 |
Примечание. Значения напряжений и модуля даны в кПа.
Определяем осадку фундамента Ф-1 по формуле (5.60):
без учета влияния Ф-2

с учетом влияния Ф-2

Определение осадки основания с использованием схемы линейно-деформируемого слоя.
Средняя осадка фундамента на слое конечной толщины (рис. 5.27) определяется по формуле [4]
где р — среднее давление под подошвой фундамента; b — ширина прямоугольного или диаметр круглого фундамента; kc и km — коэффициенты, принимаемые по табл. 5.17 и 5.18; n — число слоев, различающихся по сжимаемости в пределах расчетной толщины слоя H ; ki и ki-1 — коэффициенты, определяемые по табл. 5.19 в зависимости от формы фундамента, соотношения сторон прямоугольного фундамента и относительной глубины, на которой расположены подошвы и кровля i -го слоя (соответственно ζi = 2zi/b и ζi-1 = 2zi-1/b) ; Ei — модуль деформации i -го слоя грунта.
Формула (5.61) служит для определения средней осадки основания, загруженного равномерно распределенной по ограниченной площади нагрузкой. Эту формулу допускается применять для определения осадки жестких фундаментов.
ТАБЛИЦА 5.17. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА kc
| Относительная толщина слоя ζ´ = 2H/b | kс |
| 0 ζ´ ≤ 0,5 | 1,5 |
| 0,5 ζ´ ≤ l | 1,4 |
| 1 ζ´ ≤ 2 | 1,3 |
| 2 ζ´ ≤ 3 | 1,2 |
| 3 ζ´ ≤ 5 | 1,1 |
| ζ´ > 5 | 1,0 |
ТАБЛИЦА 5.18. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА km
| Ширина фундамента, м | km при среднем значении Е , МПа | |
| b > 10 10 ≤ b ≤ 15 b > 15 | 1 1 1 | 1 1,35 1,5 |
Расчетная толщина линейно-деформируемого слоя H (см. рис. 6.27) принимается до кровли малосжимаемого грунта (см. п. 5.1), а при ширине (диаметре) фундамента b > 10 м и среднем значении модуля деформации грунтов основания E > 10 МПа вычисляется по формуле
где H0 и ψ — принимаются соответственно равными для оснований, сложенных пылевато-глинистыми грунтами 9 м и 0,15, а сложенных песчаными грунтами 6 м и 0,1; kp — коэффициент, принимаемый; kp = 0,8 при среднем давлении под подошвой фундамента p = 100 кПа; kp = 1,2 при р = 500 кПа; при промежуточных значениях — по интерполяции.
Если основание сложено и пылевато-глинистыми, и песчаными грунтами, значение Н определяется по формуле
где Нs — толщина слоя, вычисленная по формуле (5.62) в предположении, что основание сложено только песчаными грунтами; hci — суммарная толщина слоев пылевато-глинистых грунтов в пределах от подошвы фундамента до глубины Hci равной значению Н , вычисленному по формуле (5.62) в предположении, что основание сложено только пылевато-глинистыми грунтами.
ТАБЛИЦА 5.19. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА k
| ζ = 2z/b | k для фундаментов | |||||||
| круглых | прямоугольных с соотношением сторон η = l/b | ленточных ( η ≥ 10) | ||||||
| 1 | 1,4 | 1,8 | 2,4 | 3,2 | 5 | |||
| 0,0 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 0,4 | 0,090 | 0,100 | 0,100 | 0,100 | 0,100 | 0,100 | 0,100 | 0,104 |
| 0,8 | 0,179 | 0,200 | 0,200 | 0,200 | 0,200 | 0,200 | 0,200 | 0,208 |
| 1,2 | 0,266 | 0,299 | 0,300 | 0,300 | 0,300 | 0,300 | 0,300 | 0,311 |
| 1,6 | 0,348 | 0,380 | 0,394 | 0,397 | 0,397 | 0,397 | 0,397 | 0,412 |
| 2,0 | 0,411 | 0,446 | 0,472 | 0,482 | 0,486 | 0,486 | 0,486 | 0,511 |
| 2,4 | 0,461 | 0,499 | 0,538 | 0,556 | 0,565 | 0,567 | 0,567 | 0,605 |
| 2,8 | 0,501 | 0,542 | 0,592 | 0,618 | 0,635 | 0,640 | 0,640 | 0,687 |
| 3,2 | 0,532 | 0,577 | 0,637 | 0,671 | 0,696 | 0,707 | 0,709 | 0,763 |
| 3,6 | 0,558 | 0,606 | 0,676 | 0,717 | 0,750 | 0,768 | 0,772 | 0,831 |
| 4,0 | 0,579 | 0,630 | 0,708 | 0,756 | 0,796 | 0,820 | 0,830 | 0,892 |
| 4,4 | 0,596 | 0,650 | 0,735 | 0,789 | 0,837 | 0,867 | 0,883 | 0,949 |
| 4,8 | 0,611 | 0,668 | 0,759 | 0,819 | 0,873 | 0,908 | 0,932 | 1,001 |
| 5,2 | 0,624 | 0,683 | 0,780 | 0,834 | 0,904 | 0,948 | 0,977 | 1,050 |
| 5,6 | 0,635 | 0,697 | 0,798 | 0,867 | 0,933 | 0,981 | 1,018 | 1,095 |
| 6,0 | 0,645 | 0,708 | 0,814 | 0,887 | 0,958 | 1,011 | 1,056 | 1,138 |
| 6,4 | 0,653 | 0,719 | 0,828 | 0,904 | 0,980 | 1,031 | 1,090 | 1,178 |
| 6,8 | 0,661 | 0,728 | 0,841 | 0,920 | 1,000 | 1,065 | 1,122 | 1,215 |
| 7,2 | 0,668 | 0,736 | 0,852 | 0,935 | 1,019 | 1,088 | 1,152 | 1,251 |
| 7,6 | 0,674 | 0,744 | 0,863 | 0,948 | 1,036 | 1,109 | 1,180 | 1,285 |
| 8,0 | 0,679 | 0,751 | 0,872 | 0,960 | 1,051 | 1,128 | 1,205 | 1,316 |
| 8,4 | 0,684 | 0,757 | 0,881 | 0,970 | 1,065 | 1,146 | 1,229 | 1,347 |
| 8,8 | 0,689 | 0,762 | 0,888 | 0,980 | 1,078 | 1,162 | 1,251 | 1,376 |
| 9,2 | 0,693 | 0,768 | 0,896 | 0,989 | 1,089 | 1,178 | 1,272 | 1,404 |
| 9,6 | 0,697 | 0,772 | 0,902 | 0,998 | 1,100 | 1,192 | 1,291 | 1,431 |
| 10,0 | 0,700 | 0,777 | 0,908 | 1,005 | 1,110 | 1,205 | 1,309 | 1,456 |
| 11,0 | 0,705 | 0,786 | 0,922 | 1,022 | 1,132 | 1,233 | 1,349 | 1,506 |
| 12,0 | 0,710 | 0,794 | 0,933 | 1,037 | 1,151 | 1,257 | 1,384 | 1,550 |
Примечание. При промежуточных значениях ζ и η коэффициент k определяется по интерполяции.
Значение Н , найденное по формулам (5.62) и (5.63), должно быть увеличено на толщину слоя грунта с модулем деформации E H и толщина его не превышает 0,2 H . При большей толщине слоя такого грунта, а также если лежащие выше слои имеют модуль деформации E р = 0,3 МПа, если плита опирается на слой песка толщиной 5 м с модулем деформации E = 30 МПа, который подстилается моренным суглинком, имеющим Е = 40 МПа.
Решение. Расчетную толщину слои определяем но формуле (5.62) для двух случаев: основание сложено только песчаными и только пылевато-глинистыми грунтами (при р = 0,3 МПа коэффициент kр = 1):
Тогда по формуле (5.63)
H = 8 + 7/3 = 10,3 м ≈ 10 м.
При ζ´ = 2 · 10/20 = 1 по табл. 5.17 kc = 1,4; при Е > 10 МПа и b > 15 м по табл. 5.18 коэффициент km = 1,5.
Определяем коэффициенты ki по табл. 5.19, учитывая, что η = 100/20 = 5:
Тогда по формуле (5.61)

Осадки центра, середин сторон и угловых точек прямоугольной площади размером b×l при действии на нее равномерного давления р определяются по формуле [2]:
где E — модуль деформации грунта основания, принимаемый средним в пределах сжимаемой толщи; k´ = k0 коэффициент, принимаемый по табл. 5.20 для центра прямоугольника; k´ = k1 — то же, для середины большей стороны; k´ = k2 — то же, для середины меньшей стороны; k´ = k3 — то же, для угловой точки.
Осадки поверхности основания при действии на него равномерного давления р по круглой площадке радиусом r на расстоянии R от центра этой площадки также можно определить по формуле (5.64), в которой коэффициент k´ = kr принимается по табл. 5.21 [2]. Указанным способом допускается определять осадки поверхности основания за пределами жесткого круглого фундамента.
Влияние на осадку рассчитываемого фундамента других фундаментов, нагрузок на полы и т.п. может быть оценено по формуле (5.64) с использованием схемы фиктивных фундаментов аналогично определению напряжений в основании методом угловых точек либо с помощью ЭВМ по стандартной программе. Дополнительную осадку рассчитываемого фундамента от влияния других фундаментов допускается принимать равной дополнительной осадке его центра.
ТАБЛИЦА 5.20. ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ k0, k1, k2, k3
| η | ζ´ = 2H/b | k0 | k1 | k2 | k3 | η | ζ´ = 2H/b | k0 | k1 | k2 | k3 |
| 1 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,236 0,464 0,701 0,801 0,892 0,928 0,955 | 0,045 0,109 0,236 0,436 0,482 0,564 0,601 0,628 | 0,045 0,109 0,236 0,436 0,482 0,564 0,601 0,628 | 0,024 0,056 0,115 0,231 0,305 0,380 0,416 0,444 | 3 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,801 1,019 1,238 1,338 1,420 | 0,045 0,109 0,227 0,464 0,655 0,855 0,955 1,037 | 0,045 0,107 0,225 0,400 0,510 0,656 0,742 0,815 | 0,024 0,056 0,115 0,231 0,325 0,460 0,545 0,617 |
| 1,5 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,773 0,910 1,037 1,092 1,137 | 0,045 0,109 0,236 0,446 0,564 0,682 0,737 0,783 | 0,045 0,108 0,231 0,404 0,508 0,617 0,669 0,712 | 0,024 0,056 0,115 0,231 0,323 0,426 0,478 0,518 | 5 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,454 0,801 1,028 1,310 1,456 1,592 | 0,045 0,109 0,227 0,464 0,655 0,919 1,065 1,192 | 0,045 0,107 0,225 0,400 0,511 0,656 0,752 0,852 | 0,024 0,056 0,115 0,231 0,326 0,462 0,555 0,652 |
| 2 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,792 0,974 1,128 1,201 1,265 | 0,045 0,109 0,227 0,464 0,610 0,755 0,837 0,883 | 0,044 0,107 0,225 0,403 0,514 0,641 0,708 0,762 | 0,024 0,056 0,115 0,231 0,324 0,448 0,512 0,565 | 10 | 0,2 0,5 1 2 3 5 7 10 | 0,091 0,227 0,464 0,801 1,028 1,319 1,492 1,702 | 0,045 0,109 0,227 0,464 0,655 0,928 1,110 1,310 | 0,045 0,107 0,225 0,400 0,511 0,658 0,756 0,858 | 0,024 0,056 0,115 0,231 0,326 0,463 0,558 0,659 |
ТАБЛИЦА 5.21. ЗНАЧЕНИЕ КОЭФФИЦИЕНТА kr
| ζ´ = H/r | kr при ρ = R/r | |||||||||||
| 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 2 | 2,5 | 3 | 4 | 5 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,25 | 0,12 | 0,12 | 0,12 | 0,12 | 0,05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,5 | 0,24 | 0,24 | 0,23 | 0,22 | 0,11 | 0,01 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,75 | 0,35 | 0,35 | 0,34 | 0,29 | 0,16 | 0,03 | 0,01 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,45 | 0,44 | 0,42 | 0,35 | 0,21 | 0,07 | 0,02 | 0 | 0 | 0 | 0 | 0 |
| 1,5 | 0,58 | 0,57 | 0,53 | 0,45 | 0,28 | 0,13 | 0,07 | 0,02 | 0 | 0 | 0 | 0 |
| 2 | 0,65 | 0,64 | 0,60 | 0,52 | 0,34 | 0,17 | 0,10 | 0,04 | 0,01 | 0 | 0 | 0 |
| 3 | 0,74 | 0,73 | 0,68 | 0,59 | 0,41 | 0,23 | 0,16 | 0,08 | 0,04 | 0,02 | 0 | 0 |
| 5 | 0,81 | 0,79 | 0,74 | 0,66 | 0,47 | 0,30 | 0,22 | 0,13 | 0,09 | 0,06 | 0,02 | 0,01 |
| 7 | 0,84 | 0,82 | 0,77 | 0,69 | 0,50 | 0,33 | 0,24 | 0,15 | 0,11 | 0,08 | 0,04 | 0,02 |
| 10 | 0,85 | 0,83 | 0,79 | 0,71 | 0,52 | 0,35 | 0,27 | 0,18 | 0,13 | 0,10 | 0,06 | 0,04 |
| ∞ | 0,91 | 0,89 | 0,84 | 0,76 | 0,58 | 0,40 | 0,32 | 0,23 | 0,18 | 0,15 | 0,11 | 0,09 |
ТАБЛИЦА 5.22. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА ω
| Форма загруженной площади | η | ω для определения | |||
| осадки равномерно загруженной площади | осадки абсолютно жесткого фундамента ωconst | ||||
| в угловой точке ωc | в центре ω0 | в средней ωm | |||
| Прямоугольная | 1 | 0,5 ω0 | 1,12 | 0,95 | 0,88 |
| 1,5 | 1,36 | 1,15 | 1,08 | ||
| 2 | 1,53 | 1,30 | 1,22 | ||
| 3 | 1,78 | 1,53 | 1,44 | ||
| 4 | 1,96 | 1,70 | 1,61 | ||
| 5 | 2,10 | 1,83 | 1,72 | ||
| 6 | 2,23 | 1,96 | 1,83 | ||
| 7 | 2,33 | 2,04 | 1,92 | ||
| 8 | 2,42 | 2,12 | 2,00 | ||
| 9 | 2,49 | 2.19 | 2,06 | ||
| 10 | 2,53 | 2,25 | 2,12 | ||
| Круглая | – | 0,64 | 1,00 | 0,85 | 0,79 |
Определение осадки путем непосредственного применения теории линейно-деформируемой среды. Для предварительной оценки осадок фундаментов допускается пользоваться формулой
где ω — коэффициент, принимаемый по табл. 5.22; v — коэффициент Пуассона.
Во всех случаях формула (5.65) приводит к преувеличению расчетных осадок (по сравнению с методами, рекомендуемыми нормами). Достаточно удовлетворительные результаты эта формула дает при ширине фундамента b η = l/b
Сорочан Е.А. Основания, фундаменты и подземные сооружения
Источник