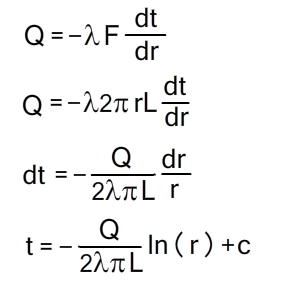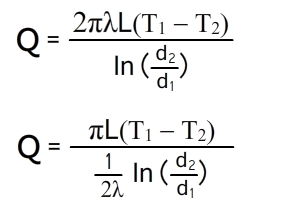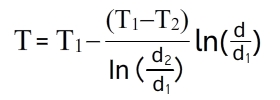Тепловые потоки через плоскую стену

Теплопроводность через стенку

Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.

Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача — величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической — по логарифмическому закону, т.е.

Q = const и T = f(x) — линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).

Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.

Теплопередача через непроницаемую стенку включает в себя следующие процессы:

1. теплоотдачу от горячей среды к стенке;
2. теплопроводность внутри стенки;
3. теплоотдачу от стенки к холодной среде.

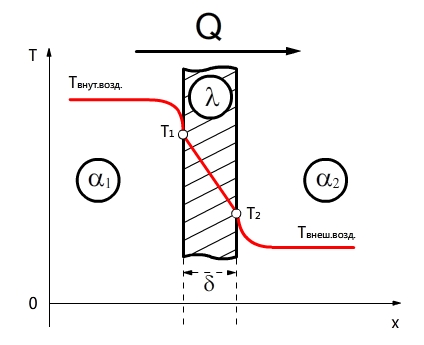
Теплопередача через плоскую стенку (граничные условия первого рода)

Теплопроводность — первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.

Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.

Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.

Тепловой поток Q [Вт] — это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).

Поверхностная плотность теплового потока рассчитывается по формуле:

где Q — тепловой поток [Вт]; F — площадь стенки [м 2 ].

На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:

где δ = dx — толщина стенки, λ

λ/δ; [Вт/м 2 *К] — коэфициент тепловой проводности стенки.

а обратная величина —

R = δ/λ; [м 2. К/Вт] — термическое сопротивление стенки.

Для теплового потока формулу так же можно представить в виде:

Общее количество теплоты проходящее через площадь стены S за время t можно представить как:

Распределение температуры в плоской стенке

Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C₁; T=C₁х+С₂ (1). Определим С₁ и С₂ через граничные условия.

При х=0 T=T₁, подставим в уравнение (1) и получим T₁=С₂.
При х=δ T=T₂, подставим в уравнение (1) и получим T₂=С₁*δ+С₂, T₂=С₁*δ+T₁, получим: С₁=(Т₂-T₁)/δ. Теперь подставим в уравнение (1) найденные С₁ и С₂, получим следующее распределение температуры в нашей стене:

Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:

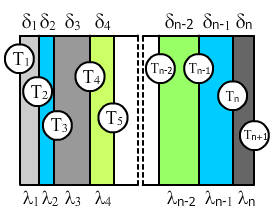
Теплопроводность через многослойную стенку

Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λ_i и разной толщиной δ_i.

Термическое сопротивление стенки считается так:

Для теплового потока формула будет иметь вид:

Температура на границе слоя вычисляется по следующей формуле:

Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:

Эквивалентная теплопроводность многослойной стенки:

Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)

Теплопередача — это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.

Коэффициент теплоотдачи α, Вт/(м 2 ·К) — это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.

Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:

q = k * (T_{возд.внутри} — T_{возд.снаружи}); Вт/м 2

Коэффициент теплопередачи для n слойной стенки:

Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:

Тогда общее термическое сопротивление теплопередаче будет равно:

Температуры на поверхности стенки можно определить по формулам:

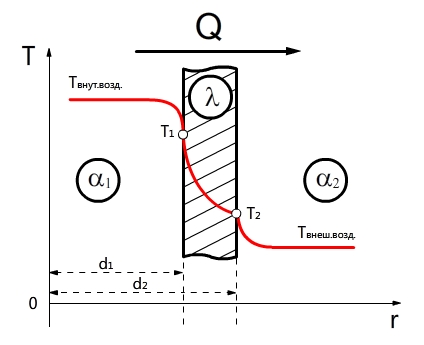
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)

Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа «труба в трубе», кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.

Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:

Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:

Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:

Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F₁ или внешней F₂ поверхности трубы. При этом расчетные формулы принимают следующий вид:

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Источник

Теплопроводность через многослойную плоскую стенку

• Теплопроводность многослойных плоских стен В тепловых устройствах стены часто состоят из нескольких плоских слоев из разных материалов. Руководство уравнение В этом случае предполагается, что все слои тесно выровнены друг с другом. Формула для расчета теплопроводности сложной стенки в стационарном состоянии может быть получена из уравнения теплопроводности.

Отдельные слои при условии, что тепловой поток через изотермическую поверхность неоднородной стенки одинаков. Чтобы решить эту проблему, рассмотрим трехслойную стенку с индивидуальной толщиной слоя 6 л, 62 т 63 и коэффициентами теплопроводности Xj, A и 3 соответственно (рис. 23-2). Межслойная

температура / с’л а Тепловой поток в каждом слое: — Q = t-0; Q =

-F (tcn — tcnY, 63 Решение этих уравнений для разности температур и сложение дает Рисунок 23-2 _ Q b; J, Q -TG t ‘sl-1sl Святой F \ 2 «Я сл F ^ г «у» В 63. Дж * В (6л j.?2 63 ‘cl-‘ cr-

—1 -: — и Откуда (23-8) F b F ч (И Я Т.е. для любого количества слоев Я = П Q = lF (t’r-rcr)) l £ f (23-9) / = 1 l * Соотношение называется термическим сопротивлением

слоя и Я = гг £ Ранг 2 ^ -Полное тепловое сопротивление многослойных плоскые и вводят эквивалентный коэффициент теплопроводности в уравнение (23-9) / я = \ т. (23-10) Сравнение уравнений (23-9) и (23-10) дает (23-11) / = п Я = н 2 £ Кк — 2 ^ j- I Эквивалентная теплопроводность многослойной стенки f равна теплопроводности однородной стенки такой же толщины, которая

их стен. ^ Иногда многослойные плоские стены рассчитываются как однородн Людмила Фирмаль

передает тот же тепловой поток при той же температуре поверхности. Значение Yaek зависит от термического сопротивления и толщины отдельных слоев. «Температура \ C между отдельными слоями сложной стены равна: (23-12) г- / ‘А- «W- ^ c \ -„. «H Hello tsl = ‘sl —- и т. д. / т лз Температура каждого слоя стенки с постоянной теплопроводностью изменяется линейно, а для многослойных плоских стенок график температуры представляет собой пунктирную

линию. Однослойная теплопроводность Цилиндрическая стена час t Наружная и внутренняя поверхности прямой цилиндрической трубки «поддерживаются при постоянной температуре / oT и / cT. Изотермическая поверхность представляет собой цилиндрическую поверхность с трубкой и осью. Поскольку температура изменяется

только в радиальном направлении, Расслоение также радиально, длина трубы бесконечна, в этом случае температурное поле одномерно. t = / (r), Где r — текущая цилиндрическая координата. Если температура неравномерно распределена по поверхности трубы, поле температуры не является одномерным, и последнее уравнение является недействительным. На фиг.23-3 показана труба с одним

• тепловым потоком, направленным радиально. Получаем отрезок трубы длины. Поверхность F на расстоянии r от оси составляет 2lg /. Температура внутренней поверхности равна / st «external- / st-. После прохождения поверхности проходит тот же постоянный тепловой поток. Рисунок 23-3 Выберите кольцевой слой в стене с радиусом r и толщиной dr. Тогда он может принять поверхность, через которую

проходит тепловой поток. Это нужно рассматривать этот базовый слой как плоскую стену. Р Фурье (А) Q = -W (ди / др), Или для кольцевого слоя Q = — \ 2nrl (дт / др). Разделение переменных dt = — (Q / 2 нМ). (Dr / r). Интегрировать уравнение (а) в диапазоне r / r> от с / м до f dt = -J ( ул tcr-tct = (Q! 2nXl) In r2 / rlt Где% Q = / (/ st-Q / (1/2 $$ Ind2 / d>. (23-13) Как видно из уравнения, распределение температуры на

азница температур между поверхностями очень мала и равна dt. По методу Людмила Фирмаль

стенке цилиндрической трубы представляет собой логарифмическую кривую. Тепловой поток через цилиндрическую стенку определяется заданными граничными условиями и зависит от отношения внешнего диаметра к внутреннему диаметру. -Тепловой поток может быть обусловлен длиной единицы qt трубы и м2 внутренней или внешней поверхности q1 и q2. • Q 2l \ (/ rm- (st) / \ nd2 / di Q 2X (/ cr

/ Jr). ндил ди ин дзфди Q 2X. (/ St-fcr) dild2 d2 (23-14) (23-15) (23-16) I1 Мне 2

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник