Центрально нагруженный фундамент пример

5.5.3. Определение основных размеров фундаментов (ч. 1)

Основные размеры фундаментов мелкого заложения (глубина и размеры подошвы) в большинстве случаев определяются исходя из расчета оснований по деформациям, который включает:

• – подсчет нагрузок на фундамент;
• – оценку инженерно-геологических и гидрогеологических условий площадки строительства; определение нормативных и расчетных значений характеристик грунтов;
• – выбор глубины заложения фундамента;
• – назначение предварительных размеров подошвы по конструктивным соображениям или исходя из условия, чтобы среднее давление на основание равнялось расчетному сопротивлению грунта, приведенному в табл. 5.13;
• – вычисление расчетного сопротивления грунта основания R по формуле (5.29), изменение в случае необходимости размеров фундамента с тем, чтобы обеспечивалось условие p ≤ R ; в случае внецентренной нагрузки на фундамент, кроме того, проверку краевых давлений;
• – при наличии слабого подстилающего слоя проверку соблюдения условия (5.35);
• – вычисление осадок основания и проверку соблюдения неравенства (5.28); при необходимости корректировку размеров фундаментов.

В случаях, оговоренных в п. 5.1, выполняется расчет основания по несущей способности. После этого производятся расчет и конструирование самого фундамента.

А. ЦЕНТРАЛЬНО НАГРУЖЕННЫЕ ФУНДАМЕНТЫ

Определение размеров подошвы фундамента по заданному значению расчетного сопротивления грунта основания. Обычно вертикальная нагрузка на фундамент N₀ задается на уровне его обреза, который чаще всего практически совпадает с отметкой планировки. Тогда суммарное давление на основание на уровне подошвы фундамента будет:

где — среднее значение удельного веса фундамента и грунта на его обрезах, принимаемое обычно равным 20 кН/м 3 ; d и А — глубина заложения и площадь подошвы фундамента.

Если принять p = R , получим следующую формулу для определения необходимой площади подошвы фундамента:

Задавшись соотношением сторон подошвы фундамента η = l/b , получим:

Зная размеры фундамента, вычисляют его объем и вес N_f , а также вес грунта на его обрезах N_g и проверяют давление по подошве:

Определение размеров подошвы фундамента при неизвестном значении расчетного сопротивления грунта основания. Как видно из формулы (5.29), расчетное сопротивление грунта основания зависит от неизвестных при проектировании размеров фундамента (глубины его заложения d и размеров в плане b×l ), поэтому обычно эти размеры определяются методом последовательных приближений. В качестве первого приближения принимают размеры фундамента по конструктивным соображениям или из условия (5.41), т.е. принимая R = R₀ .

Однако необходимые размеры подошвы фундамента можно определить за один прием. Из формулы (5.41)

ηb 2 (R – d) – N₀ = 0 ,

а с учетом формулы (5.29) при b k_z = 1)

Уравнение (5.43) приводится к виду:

для ленточного фундамента

для прямоугольного фундамента

;

;

Решение квадратного уравнения (5.44) производится обычным способом, а уравнения (5.45) — методом последовательного приближения или по стандартной программе.

После вычисления значения b с учетом модульности и унификации конструкций принимают размеры фундамента и проверяют давление по его подошве по формуле (5.42).

Пример 5.7. Определить ширину ленточного фундамента здания жесткой конструктивной схемы без подвала ( d_b = 0). Отношение L/H = 1,5. Глубина заложения фундамента d = 2 м. Нагрузка на фундамент на уровне планировки n₀ = 900 кН/м. Грунт — глина с характеристиками, полученными при непосредственных испытаниях: φ_II = 18°, c_II = 40 кПа, γ_II = γ´_II = 18 кН/м 3 , I_L = 0,45.

Решение. по табл. 5.10 имеем: γ_с1 = 1,2 и γ_с2 = 1,1; по табл. 5.11 при φ_II = 18°; М_γ = 0,43; М_q = 2,73; М_c = 5,31. Поскольку характеристики грунта приняты по испытаниям, k = 1.

Для определения ширины фундамента b предварительно вычисляем:

;

a₁ = 1,2·1,1(2,73 · 2 · 18 + 5,31 · 40) – 20 · 2 = 370,1.

Подставляя эти значения в формулу (5.44), получаем 10,22 b 2 + 370,1 b – 900 = 0, откуда

м.

Принимаем b = 2,4 м.

Пример 5.8. Определить размеры столбчатого фундамента здания гибкой конструктивной схемы ( γ_с2 = 1). Соотношение сторон фундамента η = l/b = 1,5, нагрузка на него составляет: N₀ = 4 МН = 4000 кН. Грунтовые условия и глубина заложения те же, что и в предыдущем примере.

a₀η = 1,2 · 1 · 0,43 · 18 · 1,5 = 13,93;

a₁η = [1,2 · 1(2,73 · 2 · 18 + 5,31 · 40) – 20 · 2] 1,5 = 499,22.

Затем, подставляя в уравнение (5.45) полученные величины (13,93 b 3 + 499,22 b 2 – 4000 = 0) и решая его по стандартной программе, находим b = 2,46 м, тогда l = 1,5 b = 3,7 м.

Принимаем фундамент с размерами подошвы 2,5×3,7 м.

Определение размеров подошвы фундамента при наличии слабого подстилающего слоя. При наличии в пределах сжимаемой толщи основания (на глубине z от подошвы фундамента) слоя грунта с худшими прочностными свойствами, чем у лежащего выше грунта, размеры фундамента необходимо назначать такими, чтобы обеспечивалось условие (5.35). Это условие сводится к определению суммарного вертикального напряжения от внешней нагрузки и от собственного веса лежащих выше слоев грунта ( σ_z = σ_zp + σ_zg ) и сравнению этого напряжения с расчетным сопротивлением слабого подстилающего грунта R применительно к условному фундаменту, подошва которого расположена на кровле слабого грунта.

Пример 5.9. Определить размеры столбчатого фундамента при следующих инженерно-геологических условиях (см. рис. 5.24). На площадке от поверхности до глубины 3,8 м залегают песни крупные средней плотности маловлажные, подстилаемые суглинками. Характеристики грунтов по данным испытаний: для песка φ_II = 38°, с_II = 0, γ_II = γ´_II = 18 кН/м 3 , E = 40 МПа; для суглинков φ_II = 19°, с_II = 11 кПа, γ_II = 17 кН/м 3 , E = 17 МПа. Здание — с гибкой конструктивной схемой без подвала ( d_b = 0). Вертикальная нагрузка на фундамент на уровне поверхности грунта N₀ = 4,7 MH. Глубина заложения фундамента d = 2 м. Предварительные размеры подошвы фундамента примяты исходя из R = 300 кПа (табл. 5.13) равными 3×3 м.

Решение. по формуле (5.29) с учетом табл. 5.11 и 5.12 получаем;

кПа.

Для определения дополнительного вертикального напряжения от внешней нагрузки на кровле слабого грунта предварительно находим:

среднее давление под подошвой

p = N₀/b 2 + d = 4,7 · 10 3 /3 2 + 20 · 2 = 520 + 40 = 560 кПа;

дополнительное давление на уровне подошвы

По табл. 5.4 при ζ = 2z/b = 2 · 1,8/3 = 1,2 коэффициент α = 0,606. Тогда дополнительное вертикальное напряжение па кровле слабого слоя от нагрузки на фундамент будет:

Ширина условного фундамента составит:

м.

Для условного фундамента на глубине z = 1,8 м при γ_c1 = γ_c2 = k = 1 расчетное сопротивление суглинков по формуле (5.29) будет:

R_z = 0,47 · 4 · 17 + 2,88 · 3,8 · 18 + 5,48 · 11 = 30 + 196 + 60 = 286 кПа.

Вертикальное нормальное напряжение от собственного веса грунта на глубине z = 3,8 м

Проверяем условие (5.35):

315 + 62 = 377 > R_z = 286 кПа,

т.е. условие (5.35) не удовлетворяется и требуется увеличить размеры фундамента. Расчет показал, что в данном случае необходимо принять b = 3,9 м.

Сорочан Е.А. Основания, фундаменты и подземные сооружения

Источник

Пример 9. Расчет центрально нагруженного фундамента на прочность

Определить основные размеры и рассчитать кон­струкцию ленточного сборного фундамента под наружную стену крупнопанельного жилого дома. Здание имеет подвал на отметке — 2,3 м. Вертикальная нагрузка на уровне спланированной отметки земли: нормативная N = 310 кН/м, расчетная N p = 352 кН.

Пол бетонный с цементной стяжкой, удельный вес конструкции пола γ_cf = 0,022 МН/м 3 , толщина конструкции пола 0,1 м.

Высота зда­ния H=40 м, длина L=30 м.

В основании фундамента до глуби­ны h₁ = l,7 м залегает слой песка естественной плотности p₁= 1980 кг/м 3 , а ниже этой отметки — слой глины с показателем текучести J_l=0,6, естественной плотностью р₂=1850 кг/м 3 и ко­эффициентом пористости е = 0,75. Мощность слоя 3,5 м. Уровень грунтовых вод находится на глубине 6,5 м.

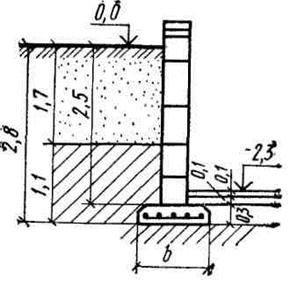Рис.24. Конструкция фундамента

Решение. Конструкция фундамента показана на рис. 24. Глу­бина заложения подошвы фундамента: d = 2,3+0,l+0,1+0,3 = 2,8 м.

Несущим слоем является глина, для которой по табл. ? нахо­дим расчетные характеристики: φ_n=14° и с_n=0,041 МПа, а по табл. ? — коэффициенты М_γ=0,29, М_q=2,17 и М_с=4,69. Соот­ношение L/H = 30/40=0,75. По табл. 1.4 находим коэффициенты γ_с1 = 1,1; γ_с2 = 1,0.Коэффициент k = 1,1, так как φ_II и с_II определены по табличным данным.

Удельный вес грунта первого и второго слоев равен соответственно:

γ₁ = 10·1980 = 0,0198 МН/м 3

γ₂ = 10·1850 = 0,0185 МН/м 3

Осредненный удельный вес грунтов, залегающих выше подошвы фундамента, определяем по формуле:

γ_II ‘ = (0,0198·1,7 + 0,0185 ·1,1) /(1,7 + 1,1) = 0,0192 МН/м 3

Приведенная глубина заложения подошвы фундамента от уров­ня пола в подвале по формуле:

d₁ = 0,4 + 0,1 (0,022/ 0,0192) = 0,515 м.

Размеры подошвы фундамента определим графически.

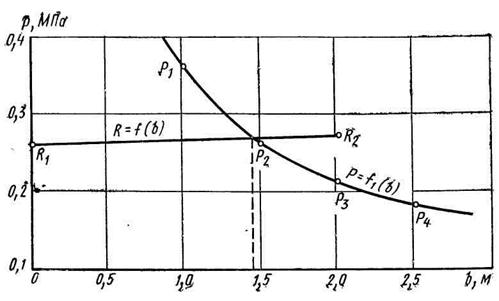
Первый график R=f(b) строим с помощью формулы (21) по двум точкам:

R₁ = 1,1·1,0/1,1 ·[2,17·0,515·0,0192 + (2,17 — 1)·2,0· 0,0192 +

+ 4,69·0,041] = 0,262 МПа;

R₂ = 1,1·1,0/1,1 · [0,29·1·2·0,0185 + 2,17·0,515·0,0192 + (2,17— 1) ·2,3·0,0192 + 4,69·0,041] = 0,276 МПа.

Затем в формулу:

подставим несколько последовательно увеличивающихся значений b и постоянное значение βγ_фd= 0,02·2,8=0,056 МПа. В результате получим точки, по которым постро­им график второй функции p=f(b):

р = 0,310/1·1+0,056 = 0,366 МПа;

р = 0,310/1,5·1 +0,056 = 0,263 МПа;

р = 0,310/2·1 + 0,056 = 0,211 МПа;

р= 0,310/2,5·1 + 0,056 = 0,18 МПа.

Полученные данные наносим на график, показанный на рис. 25. Точка пересечения двух линий дает искомое значение b = 1,45 м. Примем ближайшую ширину b =1,4 м, которая соответ­ствует ширине железобетонной плиты марки Ф14.

Рис. 25. График к примеру 9

Расчетное сопротивление грунта основания для принятой ши­рины подошвы фундамента:

R = 1,1· 1,0/1,1 [0,29·1·1,4·0,0185 + 2,17·0,515·0,0192 +

+ (2,17 — 1) ·2,0·0,0192 + 4,69·0,041] = 0,273 МПа.

Вес 1 м фундаментной плиты:

G_ф= 10·2180 /2,38 =0,0092 МН.

Вес стены подвала, состоящей из четырех блоков ФС6 и одного блока ФСН6:

G_с= 4·10·1960 /2,38 + 10·490/1,18 = 0,037 МН.

Р — вес грунта на обрезе фундамента (рис. 22.):

Р = 0,0198·1,7·0,4+ 0,0185·0,8·0,4=0,0194 МН.

Среднее давление под подошвой фундамента:

Р _ср = (0,310 + 0,0092 + 0,037 + 0,0194) /1,4· 1= 0,268 МПа.

Условие Р _ср р = 1,1 (0,0092 + 0,037) = 0,0508 МН;

G_гр р = 1,2·0,0194 = 0,0233 МН.

Давление под подошвой фундамента от действия расчетных на­грузок по формуле (29):

Р_ср р =(0,352+0,0508+0,0233)/1,4·1=0,304МПа
Поперечная сила в сечении фундамента у грани стены по фор­мулам (30,31):

Q = 0,304·1 (1,4 – 0,6) /2 = 0,12 МН.

Проверяем выполнение условий (32, 33), предварительно опреде­лив по таблице … [СНиП] R_bt = 0,75 МПа:

Условие выполняется, следовательно, установка поперечной арма­туры и ее расчет не требуются.

Проверяем выполнение условия (34):

Q = 0,304 [0,5 (1,4 — 0,6)— 0,135] 1 = 0,081 2 /0,135 = 0,585 МН.

Определяем расчетную продавливающую силу по формулам (38,39):

F = 0,304 (1,4 – 0,6 – 2 ·0,265) /2 = 0,082MH.

Из этих же формул u_m=0,5 (1 + 1) = 1 м.

Проверяем прочность фундамента на продавливание по усло­вию (35):

0,082 2 ·1 = 0,0243 МН·м.

В качестве рабочих стержней примем арматуру класса А-II с расчетным сопротивлением Rs = 280 МПа (табл. V.4).

Определим требуемую площадь сечения арматуры на 1 м дли­ны плиты по формулам (42, 43):

А_s= 0,0243/0,9.0,265·280 = 0,00036 м 2 = 3,6 см 2 .

По табл. V.5 принимаем пять стержней диаметром 10 мм из стали класса А-II (5 Ø 10 А-II) с А_s = 3,93 см 2 . Шаг стержней и = 20 см (рис.24).

Площадь распределительной арматуры A_sp = 0,1 · 3,93 = 0,393 см 2 .

В ленточном фундаменте на изгиб совместно работают две консоли, поэтому увеличим вдвое площадь распределительной арматуры|
A_Sp=0,786 см 2 , принимаем пять стержней диаметром 6 мм из
стали класса A-I (5 Ø 6 A-I) с A_sp = l,42 см 2 . Шаг распределительных стержней u = 30 см. ..

Изгибающий момент от нормативной нагрузки у грани стены по формулам (40,41):

М= 0,125·0,268(1,4 —0,6) 2 ·1=0,021 МН-м.

По табл. V.3 и V.4 находим значения модулей упругости арма­туры и бетона: Е_s=210000 МПа и Е_b = 20500 МПа и определяем соотношение n=210000/20500 =10,2.

Коэффициент армирования сечения:

μ₁ = 3,93/30·100 = 0,0013 = 0,13% > 0,05%.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник