Упругое основание для фундамента

К расчету балок на упругом основании

В малоэтажном строительстве, как впрочем и в любом другом, балки на упругом основании встречаются намного чаще, чем это можно подумать. По той причине, что любой ленточный фундамент, а иногда и плитный фундамент можно рассматривать как балку на упругом основании.

И если с расчетом балки — ленточного фундамента проблем практически не возникает по той простой причине, что нагрузка на ленточный фундамент как правило равномерно распределенная, а значит и фундамент ведет себя, как абсолютно жесткая балка, дополнительных расчетов не требующая. То при рассмотрении участка плитного фундамента как балки или ленточного фундамента с неравномерно приложенной нагрузкой могут возникнуть некоторые проблемы.

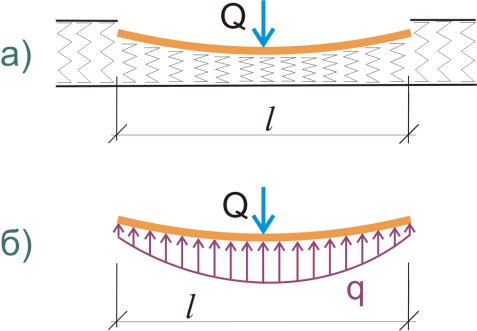
Дело в том, что на сегодняшний день не существует идеальной модели упругого основания. Одной из наиболее распространенных является модель Фусса-Винклера, согласно которой опорная реакция упругого основания, другими словами — распределенная нагрузка q, действующая на балку, является не равномерно распределенной, а пропорциональной прогибу балки f в рассматриваемой точке:

q = — kf (393.1)

k = k_оb (393.2)

k_о — коэффициент постели, постоянный для рассматриваемого основания и характеризующий его жесткость, измеряется в кгс/см 3 .

b — ширина балки.

Рисунок 393.1 а) модель балки на сплошном упругом основании, б) реакция основания q на действующую сосредоточенную нагрузку.

Из этого можно сделать как минимум два вывода, неутешительных для человека, собравшегося по-быстрому рассчитать фундамент небольшого домика, к тому же даже основы теоретической механики и теории сопротивления материалов постигшего с трудом:

1. Расчет балки на упругом основании — это статически неопределимая задача, так как уравнения статики позволяют лишь определить суммарное значение нагрузки q (реакции основания). Распределение нагрузки по длине балки будет описываться достаточно сложным уравнением:

q/EI = d 4 f/dx 4 + kf/EI (393.3)

которое мы здесь решать не будем.

2. Помимо всего прочего при расчете таких балок необходимо знать не только коэффициент постели основания, но и жесткость балки ЕI, т.е. все параметры балки — материал, ширина и высота сечения, должны быть известны заранее, между тем при расчете обычных балок определение параметров и является основной задачей.

И что в этом случае делать простому человеку, не обремененному глубокими знаниями сопромата, теорий упругости и прочих наук?

Ответ простой: заказать инженерно-геологические изыскания и проект фундамента в соответствующих организациях. Да, я понимаю, что при этом стоимость дома может увеличиться на несколько тысяч $, но все равно это оптимальное решение в таком случае.

Если же вы, не смотря ни на что, хотите сэкономить на геологоразведке и расчете, т.е. выполнить расчет самостоятельно, то будьте готовы к тому, что придется больше средств потратить на фундамент. Для такого случая я могу предложить следующие расчетные предпосылки:

1. Как правило сплошная фундаментная плита принимается в качестве фундамента в тех случаях, когда несущая способность основания очень низкая. Другими словами грунт — это песок или глина, никак не скальные породы. Для песка, глины и даже гравия коэффициент постели, определенный опытным путем в зависимости от различных факторов (влажности, крупности зерен и др.) k_o = 0.5-5 кгс/см 3 . Для скальных пород k_o = 100-1500 кг/см 3 . Для бетона и железобетона k_o = 800-1500 кгс/см 3 . Как видно из формулы 393.1, чем меньше значение коэффициента постели, тем больше будет прогиб балки при той же нагрузке и параметрах балки. Таким образом мы можем для упрощения дальнейших расчетов предположить, что слабые грунты не влияют на прогиб балки, точнее этим незначительным влиянием можно пренебречь. Другими словами изгибающие моменты, поперечные силы, углы поворотов поперечных сечений и прогибы будут такими же, как и у балки, загруженной распределенной нагрузкой. Результатом такого допущения будет повышенный запас прочности и чем больше будут прочностные характеристики грунтов, тем большим будет запас прочности.

2. Если сосредоточенные нагрузки на балку будут симметричными, то для упрощения расчетов реакцию упругого основания можно принимать равномерно распределенной. Основанием для такого допущения служат следующие факторы:

2.1. Как правило фундамент, рассматриваемый как балка на упругом основании, в малоэтажном строительстве имеет относительно небольшую длину — 10-12 м. При этом нагрузка от стен, рассматриваемая как сосредоточенная, в действительности является равномерно распределенной на участке, равном ширине стен. Кроме того балка имеет некоторую высоту, на первом этапе расчета не учитываемую, а между тем даже сосредоточенная нагрузка, приложенная к верху балки, будет распределяться в теле балки и чем больше высота балки, тем больше площадь распределения. Так например для фундаментной плиты высотой 0.3 м и длиной 12 м, рассматриваемой как балка, на которую опираются три стены — две наружных и одна внутренняя, все толщиной 0.4 м, нагрузки от стен более правильно рассматривать не как сосредоточенные, а как равномерно распределенные на 3 участках длиной 0.4 + 0.3·2 = 1 м. Т.е. нагрузка от стен будет распределена на 25% длины балки, а это не мало.

2.2. Если балка лежащая на сплошном упругом основании имеет относительно небольшую длину и к ней приложено несколько сосредоточенных нагрузок, то реакция основания будет изменяться не от 0 в начале длины балки до некоего максимального значения посредине балки и опять до 0 в конце длины балки (для варианта показанного на рис. 393.1), а от некоторого минимального значения до максимального. И чем больше сосредоточенных нагрузок будет приложено к балке относительно небольшой длины, тем меньше будет разница между минимальным и максимальным значением опорной реакции упругого основания.

Результатом принятого допущения будет опять же некоторый запас прочности. Впрочем в данном случае возможный запас прочности не превысит нескольких процентов. Например, даже для однопролетной балки, на которую действует распределенная нагрузка, равномерно изменяющая от 1.5q в начале балки до 0.5q в середине балки и снова до 1.5q в конце балки (см. статью «Приведение распределенной нагрузки к эквивалентной равномерно распределенной») суммарная нагрузка составит ql, как и для балки, на которую действует равномерно распределенная нагрузка. Между тем максимальный изгибающий момент для такой балки составит

М = ql 2 /(8·2) + ql 2 /24 = 10ql 2 /96 = ql 2 /9.6

Это на 20% меньше, чем для балки, на которую действует равномерно распределенная нагрузка. Для балки, изменение опорной реакции которой описывается достаточно сложным уравнением, особенно если сосредоточенных нагрузок будет много, разница будет еще меньше. Ну и не забываем про п.2.1.

В итоге при использовании данных допущений задача расчета балки на сплошном упругом основании максимально упрощается, особенно при симметричности приложенных нагрузок, несимметричные нагрузки приведут к крену фундамента и этого в любом случае следует избегать. Более того на расчет практически не влияет количество приложенных сосредоточенных нагрузок. Если для балки на шарнирных опорах вне зависимости от их количества должно соблюдаться условие нулевого прогиба на всех опорах, что увеличивает статическую неопределимость балки на количество промежуточных опор, то при расчете балки на упругом основании достаточно рассматривать прогиб, как нулевой, в точках приложения крайних сосредоточенных нагрузок — наружных стен. При этом прогиб под сосредоточенными нагрузками — внутренними стенами определяется согласно общих уравнений. Ну а определить осадку фундамента в точках, где прогиб принят нулевым, можно, воспользовавшись существующими нормативными документами по расчету оснований и фундаментов.

А еще можно достаточно просто подобрать длину консолей балки таким образом, чтобы прогиб и под внутренними стенами был нулевым. Пример того, как можно воспользоваться данными расчетными предпосылками, рассказывается отдельно.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Основы строймеха и сопромата . Балки

Оценка пользователей: Нет Переходов на сайт: 3356 Комментарии:

Добрый день! Пытаюсь рассчитать свой ленточный фундамент. Размеры в плане 10х10м. Ширина 0,4м Высота 1м. Равномерно распределенная нагрузка 5т/м Пытаюсь рассчитать продольную рабочею арматуру. Пользуюсь формулами из пособия по СП 52-101-2003 Там есть формула для нахождения Am. Для данной формулы необходимо найти изгибающий момент. Можно ли использовать вашу формулу для нахождения изг момента для балки на упругом оснвании М=q*lквадрат/9,6 На форумах говорят слишком уж большой момент будет.

Ваш вопрос достаточно сложный и я по этому поводу давно собираюсь написать соответствующую статью, но все руки не доходят. Поэтому попробую тезисно.
Вообще-то если нагрузка от здания равномерно распределенная, а физико-химические свойства основания постоянны, то никакого продольного армирования для ленточного фундамента не требуется (смотрите второй абзац).
Тем не менее и равномерно распределенная нагрузка и однородное основание возможны только в теории. На практике же основание состоит из различных пород, залегающих слоями, различной толщины и под различными углами, но даже в этих слоях свойства пород меняются. К тому же еще есть грунтовые воды, сезон замерзания и оттаивания, карстовые процессы и прочие неожиданности. Даже геологоразведка позволяет определить свойства основания лишь приблизительно. Да и нагрузка является равномерно распределенной достаточно условно. Поэтому армирование фундаментной стены никогда не помешает. А вот какую расчетную схему для этого выбрать — это отдельный вопрос. Принимая для расчета армирования нижней зоны поперечного сечения момент М=q*l^2/9,6, вы допускаете, что ваш ленточный фундамент будет иметь опоры только в углах (если рассматривать его как однопролетную балку), а под остальным фундаментом грунт или вымоется или просядет сильнее чем под углами. Что хотя теоретически и возможно, но все равно маловероятно, так как при этом нагрузки в углах — опорные реакции балки -возрастают значительно и значит грунт в углах тоже скорее всего просядет.
Если же вы будете использовать подобное значение момента для расчета армирования верхней зоны поперечного сечения фундамента, то это будет не совсем корректно, но для упрощения расчетов допустимо. Тем более, что чаще всего фундаменты проседают в углах зданий, что приводит к трещинам в стенах из материалов, плохо работающих на растяжение. Хотя и запас прочности при этом получится скорее всего не малый.
Кроме того подобные расчеты подразумевают, что бетонировать фундамент вы будете сразу, без технологических перерывов, чтобы обеспечить монолитность балки. Примерно так.

Спасибо за ответ! Если я правильно понимаю в расчете рабочей продольной арматуры все упирается в нахождении максимального изгибающего момента в фундаменте? Зная его можно пользоваться формулами из пособия к СП 52-101-2003. У вас расчет плиты перекрытия http://doctorlom.com/item220.html сделан по формулам из данного пособия. По ним и я хотел считать. Но для балок http://doctorlom.com/item170.html у вас другая методика расчета. Какую лучше использовать для расчета ленточного фундамента.

Оба метода построены на одних и тех же теоретических предпосылках и дают практически одинаковый результат. так что можете пользоваться тем, который вам больше нравится.

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

9.2. ОПРЕДЕЛЕНИЕ УПРУГИХ И ДЕМПФИРУЮЩИХ ХАРАКТЕРИСТИК ОСНОВАНИЯ ДЛЯ РАСЧЕТА ФУНДАМЕНТОВ

9.2.1. Коэффициенты жесткости и демпфирования для фундаментов на естественном основании

Основным параметром, характеризующим упругие свойства оснований фундаментов, является коэффициент упругого равномерного сжатия С_z . Его следует определять экспериментально. При отсутствии экспериментальных данных величину С_z , кН/м 3 , допускается определять для фундаментов с площадью подошвы А не более 200 м 2 по формуле

где b₀ — коэффициент, м –1 , принимаемый равным: для песков 1, для супесей и суглинков 1,2, для глин и крупноблочных грунтов 1,5; E — модуль деформации грунта, кПа, определяемый в соответствии с требованиями главы СНиП «Основания здании и сооружений. Нормы проектирования»; A — площадь подошвы фундамента, м 2 ; А₀ = 10 м 2 .

Модуль деформации грунта, как правило, должен определяться по результатам полевых штамповых испытаний. При отсутствии таких испытаний допускается пользоваться табличными данными.

Для фундаментов с площадью подошвы А , превышающей 200 м 2 , значение коэффициента C_z принимается как для фундаментов с площадью подошвы A = 200 м 2 .

Коэффициент С_z характеризует жесткость основания при поступательном вертикальном перемещении фундамента.

Помимо С_z в расчетах используются коэффициент упругого неравномерного сжатия С_φ , кН/м 3 (при повороте фундамента относительно горизонтальной оси, проходящей через его подошву), упругого равномерного сдвига С_x , кН/м 3 (при горизонтальном поступательном перемещении фундамента), и упругого неравномерного сдвига С_ψ , кН/м 3 (при вращении относительно вертикальной оси). Их значения принимаются [1]:

Коэффициенты жесткости для естественных оснований фундаментов определяются по формулам:

– при вертикальных поступательных колебаниях фундамента,

– при горизонтальных поступательных колебаниях фундамента

– при вращательных колебаниях относительно горизонтальной оси, проходящей через подошву фундамента,

– при вращательных колебаниях относительно вертикальной оси, проходящей через центр тяжести подошвы фундамента,

где I_φ и I_ψ — моменты инерции подошвы фундамента относительно горизонтальной и вертикальной осей.

Основной причиной, определяющей затухания колебаний фундаментов, является потеря энергии на возбуждение упругих волн в грунте, которые переносят энергию от фундамента в отдаленные от него части грунтового массива, где эта энергия постепенно поглощается за счет неупругого сопротивления грунта. Однако при описании колебаний самого фундамента учет потерь энергии за счет излучения упругих волн удобнее вести в рамках теории вязкого сопротивления, которое зависит от тех же параметров, что и жесткость естественного основания, т.е. от вида грунта, его упругих свойств и площади подошвы. Следовательно, коэффициенты демпфирования и коэффициенты жесткости для естественных оснований связаны между собой [2]. Демпфирующие свойства определяются коэффициентами относительного демпфирования ξ (доля критического затухания колебаний), определяемыми, как правило, по результатам испытаний.

Коэффициент относительного демпфирования для вертикальных колебаний ξ_z связан с коэффициентом демпфирования упруго-вязкого основания B_z в уравнении (9.4) следующим образом:

где λ_z — угловая частота свободных вертикальных колебаний установки.

При отсутствии экспериментальных данных коэффициент относительного демпфирования при вертикальных колебаниях фундамента допускается определять по формулам:

– для установившихся (гармонических) колебаний

– для неустановившихся (импульсных) колебаний

где р — среднее статическое давление, кПа, на основание под подошвой фундамента от расчетных статических нагрузок при коэффициенте перегрузки, равном 1.

Значения ξ_z , рассчитанные по формуле (9.13), примерно в 1,5 раза меньше, чем полученные по формуле (9.14). Значения ξ_z вычисляются по формуле (9.13) при определении амплитуд вынужденных установившихся колебаний и при определении темпа уменьшения амплитуд свободных колебаний фундамента в конце процесса колебаний (ориентировочно после двух-трех циклов свободных колебаний, возбужденных некоторой причиной — ударом, импульсом, начальным отклонением и т.п.). Формула (9.14) применима для оценки наибольших перемещений фундамента при свободных колебаниях под действием импульса. Меньшие значения ξ_z , вычисляемые по формуле (9.13), учитывают частичный возврат энергии колеблющемуся фундаменту упругими волнами, отразившимися от более плотных глубоких слоев грунта.

Значения коэффициентов относительного демпфирования для горизонтальных колебаний ξ_x и вращательных колебаний относительно горизонтальной ξ_φ и вертикальной ξ_ψ осей принимаются:

Если из опытов известны модули затухания Ф , с, колебаний фундаментов [7], то коэффициенты относительного демпфирования можно вычислить по формуле

где λ_z, λ_x, λ_φ, λ_ψ — соответственно угловые чистоты свободных колебаний фундамента — вертикальных, горизонтальных и вращательных относительно горизонтальной и вертикальной осей.

9.2.2. Коэффициенты жесткости и демпфирования для свайных фундаментов. Определение приведенной массы

При определении податливости свай в вертикальном направлении принята расчетная схема в виде сжимаемого стержня в упругой винклеровой среде, препятствующей вертикальным перемещениям каждого сечения стержня (вдоль его оси); торец стержня опирается на пружину.

Ниже даны формулы для определения приведенной массы m_red свайного фундамента и приведенных коэффициентов жесткости k_φ,red, k_x,red, k_ψ,red , которые используются в расчетах вертикальных, горизонтально-вращательных и крутильных колебаний фундаментов во всех формулах вместо массы m (фундамента и машины) и коэффициентов жесткости k_z, k_φ, k_x, k_ψ .

Для вертикальных колебаний фундаментов:

где m_r — общая масса ростверка с установленной на нем машиной, т; m_pi — масса i -й сваи, т; N — число свай; β * = k₂[0,2 + 0,8th(6/l)] ; th — тангенс гиперболический; С * z — коэффициент упругого равномерного сжатия грунта на уровне нижних концов свай, кН/м 3 , определяемый по формуле (9.6), в которой А принимается равной площади поперечного сечения сваи, а значение b₀ для забивных свай удваивается; E_bt — начальный модуль упругости бетона, кПа, принимаемый в соответствии с главой СНиП «Бетонные и железобетонные конструкции. Нормы проектирования»; l — длина свай, м; d — длина стороны поперечного сечения сваи, м; k₁ коэффициент, учитывающий упругое сопротивление грунта по боковой поверхности сваи; принимается равным 3 · 10 2 кПа 1/2 · м –1/2 ; k₂ — коэффициент, учитывающий влияние свойств прорезаемого сваей грунта на приведенную массу свайного фундамента, принимается равным 2.

Для горизонтально-вращательных колебаний фундаментов:

где θ_r — момент инерции массы ростверка и машины относительно горизонтальной оси, проходящей через их общий центр перпендикулярно плоскости колебаний, т·м 2 ; h₀ — расстояние от центра массы m_r до подошвы ростверка, м; r_i — расстояние от оси i -й сваи до оси поворота подошвы фундамента, м; k_z,red — приведенный коэффициент жесткости свайного фундамента, кН/м, определяемый по формуле (9.18).

Для горизонтальных колебаний фундаментов приведенная масса фундамента m_red определяется по формуле (9.17), как и для вертикальных колебаний, при k₂ = 2/3. Коэффициент жесткости при упругом равномерном сдвиге, кН/м, определяется по формуле

где E_btI — жесткость поперечного сечения сваи на изгиб, кПа·м 4 ; α´ — коэффициент упругой деформации системы «свая-грунт»: α´ = 1,6 α_d (здесь α_d — коэффициент деформации сваи, определяемый как и при расчете свай на статические горизонтальные нагрузки).

Значения коэффициента q вычисляются следующим образом:

– для свай, шарнирно сопряженных с низким ростверком, и для свай, защемленных в низкий ростверк, по формулам:

– для свай, шарнирно сопряженных с высоким ростверком, и для свай, защемленных в высокий ростверк, по уравнениям:

Источник