Великая стена
У короля Людовика двое сыновей. Они ненавидят друг друга, и король боится, что после его смерти страна будет уничтожена страшными войнами. Поэтому Людовик решил разделить свою страну на две части, в каждой из которых будет властвовать один из его сыновей. Он посадил их на трон в города A и B, и хочет построить минимально возможное количество фрагментов стены таким образом, чтобы не существовало пути из города A в город B.
Страну, в которой властвует Людовик, можно упрощенно представить в виде прямоугольника m×n. В некоторых клетках этого прямоугольника расположены горы, по остальным же можно свободно перемещаться. Кроме этого, ландшафт в некоторых клетках удобен для строительства стены, в остальных же строительство невозможно.
При поездках по стране можно перемещаться из клетки в соседнюю по стороне, только если ни одна из этих клеток не содержит горы или построенного фрагмента стены.
Входные данные
В первой строке входного файла содержатся числа m и n (1 ≤ m, n ≤ 50). Во второй строке заданы числа k и l, где 0 ≤ k, l, k + l ≤ m·n—2, k – количество клеток, на которых расположены горы, а l – количество клеток, на которых можно строить стену. Естественно, что на горах строить стену нельзя. Следующие k строк содержат координаты клеток с горами xi и yi, а за ними следуют l строк, содержащие координаты клеток, на которых можно построить стену – xj и yj. Последние две строки содержат координаты городов A (xA и yA) и B (xB и yB) соответственно. Среди клеток, описанных в этих k+l+2 строках, нет двух совпадающих. Гарантируется, что 1 ≤ xi, xj, xA, xB ≤ m и 1 ≤ yi, yj, yA, yB ≤ n.
Выходные данные
В первой строке выходного файла должно быть выведено минимальное количество фрагментов стены F, которые необходимо построить. В последующих F строках необходимо вывести один из возможных вариантов застройки.
Если невозможно произвести требуемую застройку, то необходимо вывести в выходной файл единственное число -1.
Источник
Задачка от Джеффа Безоса. На размышление даётся 30 секунд
Считается, что её могут загадать на собеседовании в «Амазон».
Перед вами очередная задачка с собеседований в крупные IT-компании. Вот сама задача:
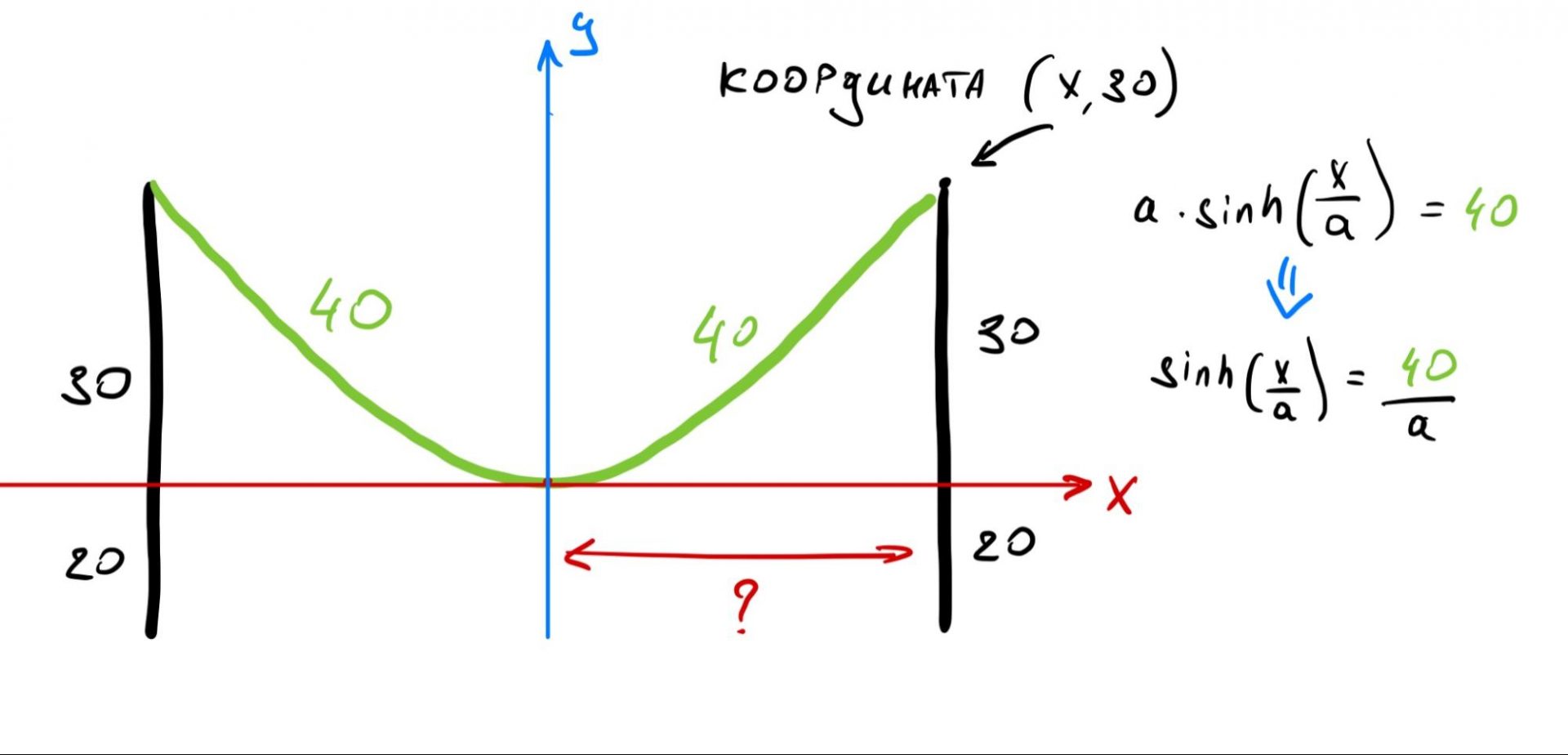
Кабель длиной 80 метров висит на двух столбах. Высота каждого столба — 50 метров. Каково расстояние между столбами, если центр провисающего кабеля находится:
а) на высоте 20 метров от земли — вариант для технарей;
б) на высоте 10 метров от земли — вариант для гуманитариев.
Для решения можно использовать инженерный калькулятор с расширенными функциями.
В задаче нет никакого подвоха, но для решения нужно хорошо знать математику, углы и угловые функции. Попробуйте сначала решить её самостоятельно, а потом загляните в решения.
Первое, что мы сделаем, — поднимем уровень земли, чтобы он касался провода. Так как до центра провиса 20 метров, то высота столбов тоже уменьшится на эти 20 метров:
Расстояние между столбами у нас при этом осталось тем же самым.
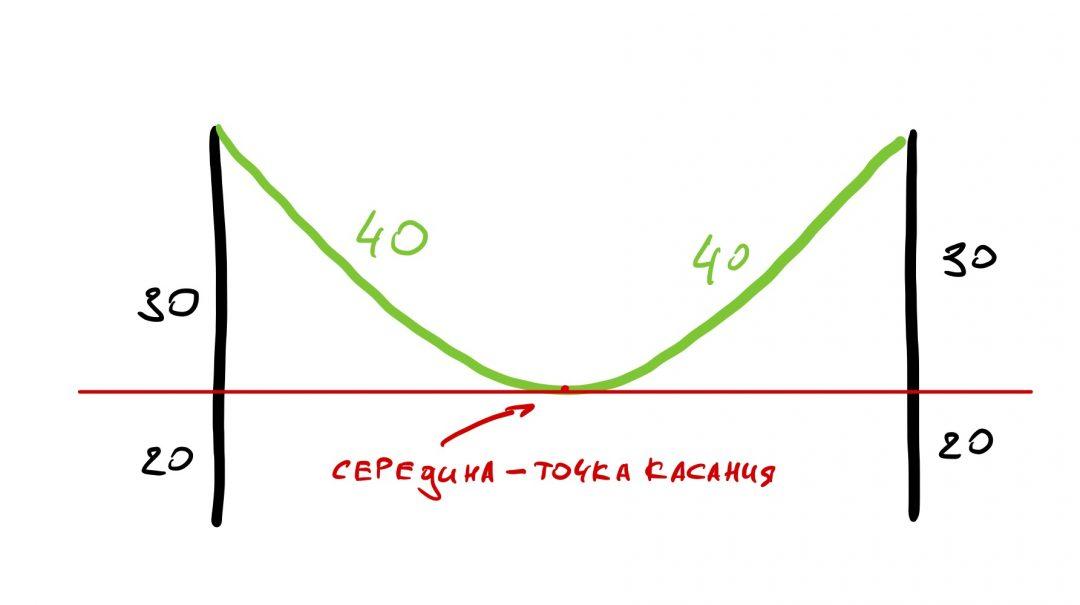
Так как кабель провисает по центру, нам достаточно найти расстояние от края до середины и умножить его на 2 — так мы найдём полное расстояние между столбами.
❗️ Самая важная часть.
Так как провисающий кабель похож на гиперболу, то мы для решения будем использовать не тригонометрические функции, которые работают с прямыми и окружностями, а гиперболические, график которых похож на гиперболу.
Если нужно точно описание этих функций — вот оно:
Сначала поработаем с высотой столба. Запишем формулу для расстояния, затем добавим на рисунок те данные, которые мы уже знаем, и раскроем формулу:
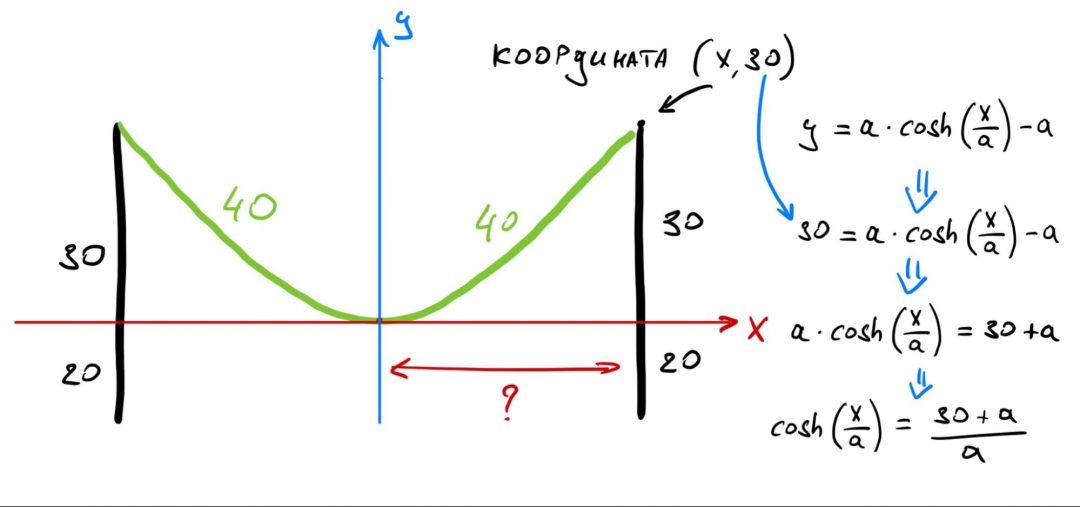
Теперь составим второе уравнение, в котором используем значение длины кабеля. Так как он провисает ровно посередине, то его длина от края до точки перегиба — 40 метров.
Добавляем свойство о том, что разность квадратов гиперболического синуса и косинуса равна единице:
Раскрываем скобки, приводим всё к классическому квадратному уравнению, и, решая его, получаем ответ: a = 35/3.
Это значение подставляем в формулу гиперболического синуса, чтобы посчитать половину длины кабеля:
Решаем это уравнение на калькуляторе и получаем ответ: x ≈ 22,7. Это половина расстояния между столбами, а полное расстояние ≈ 45,4 метра.
Ответ: если высота до центра провиса равна 20 метров, то расстояние между столбами составляет примерно 45,4 метра.
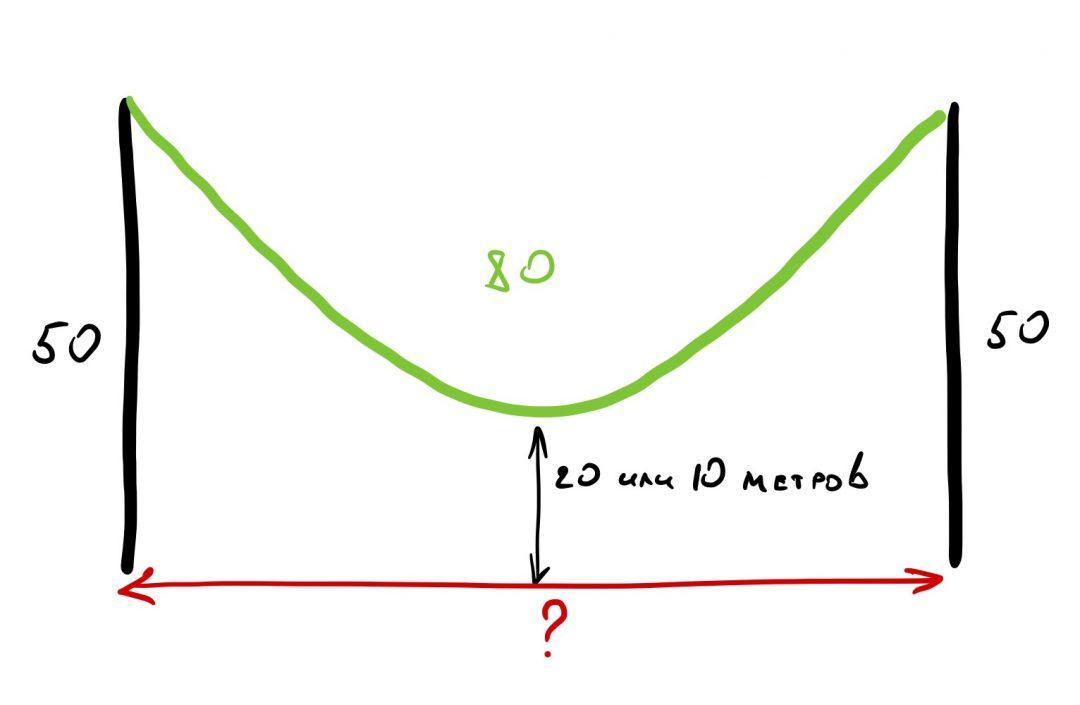
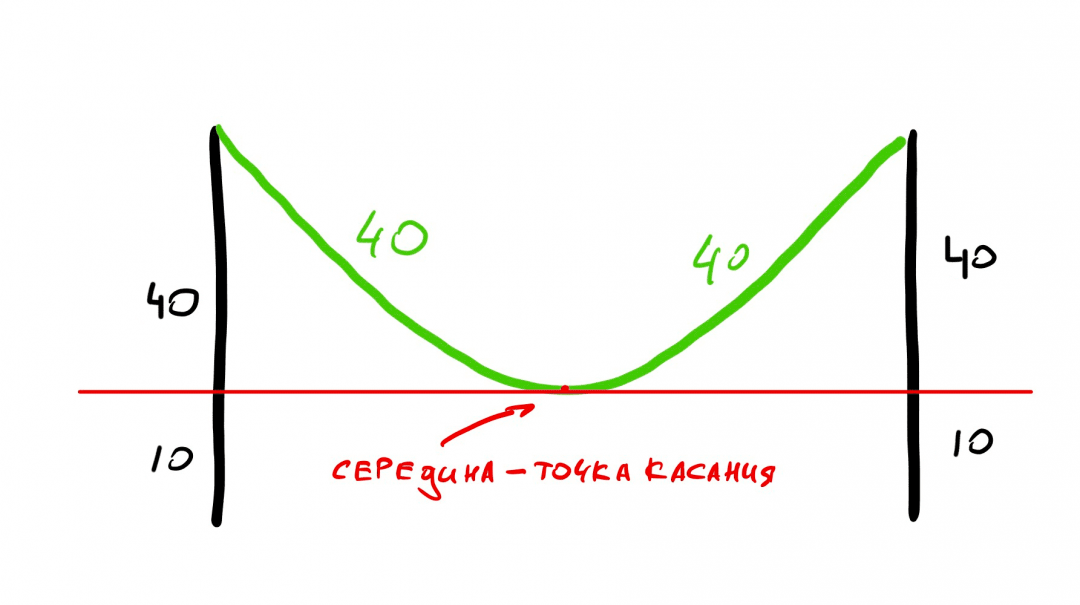
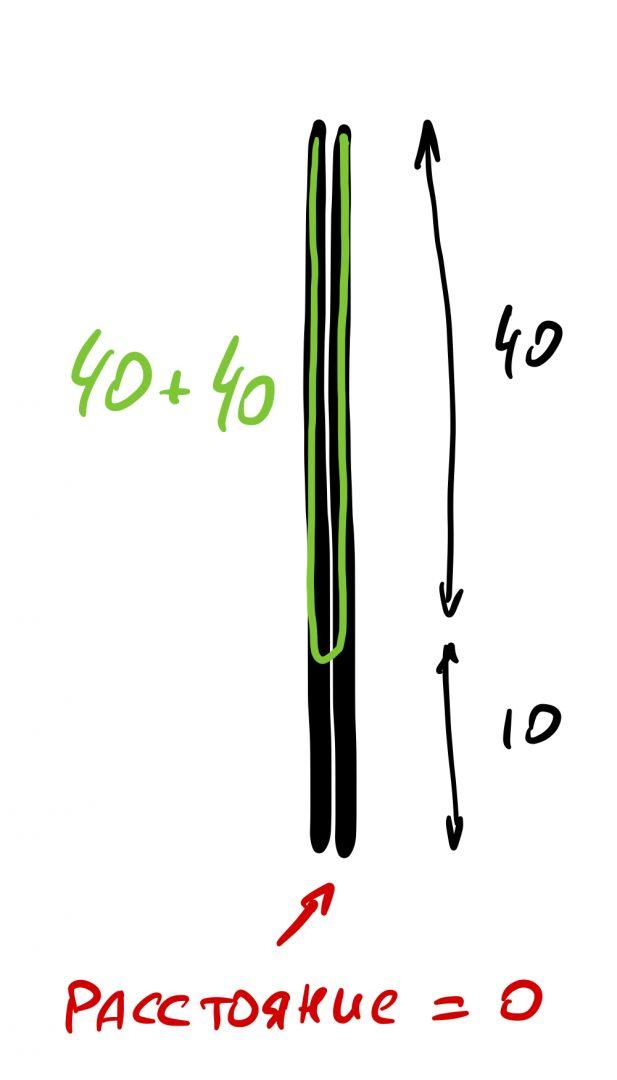
У гуманитариев кабель длиной 80 метров провисает на минимальной высоте 10 метров от земли. При этом высота столба 50 метров. Значит, если провести новый «уровень земли» (красным), верхняя часть столба будет равняться 40 метрам.
Посмотрите на рисунок. Нет ли здесь ошибки?
Если верхняя часть столба 40 метров и длина кабеля до середины — тоже 40 метров, то какой это треугольник? Может ли такой треугольник существовать?
И в чём тут мораль, Код?
В смысле мораль? Это математическая задачка с подвохом, зачем тут мораль?
Источник
Как лучшие умы 200 лет решали логическую задачку, у которой. нет решения
Издавна среди жителей старого Кенигсберга была в ходу такая головоломка: как так исхитриться и пройти по всем городским мостам через реку Преголя, чтобы не пройти ни по одному из них дважды. Не один мозг был сломан в попытках решить эту задачу как теоретически, так и во время прогулок. Более того, доказать или опровергнуть возможность существования такого маршрута никто тоже не мог. Попробуйте сами, может вам удастся найти тот самый путь?
Так и жили бедные горожане без решения, пока в 1736 году талантливый во всех смыслах член Петербургской академии наук Леонард Эйлер, внесший существенный вклад в становление российской науки, научно обосновал невозможность решения этой задачи.
Итак, для начала нарисуем упрощенную схему города в виде математического графа. Его ребра у нас будут соответствовать мостам — их всего семь, — а частям города — вершины нашего графа. В процессе решения задачи Эйлер пришел к следующим выводам:
- Не существует такого графа, который имел бы нечетное число нечетных же вершин
- Если все вершины графа четные, то можно начертить его без отрыва карандаша от бумаги, при этом начало и конец могут быть в одной вершине
- Если две вершины графа нечетные, то этот граф можно начертить без отрыва карандаша от бумаги, но в таком случае начало будет в одной нечетной вершине, а конец — в другой
- У графа кенигсбергских мостов все вершины были нечетными, из чего следовало, что невозможно пройти по всем мостам, не проходя ни по одному из них дважды
Благодаря семи кенигсбергским мостам Эйлер изобрел математические циклы имени себя. Эйлеров цикл — это замкнутый путь, проходящий через каждое ребро графа ровно по одному разу. Согласно теореме, эйлеров цикл существует тогда и только тогда, когда граф связный (между любой парой вершин графа есть как минимум один путь) или будет являться связным, если удалить из него все изолированные вершины, и в нем отсутствуют вершины нечетной степени.
Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечетной степени.
Но на этом история с семью кенигсбергскими мостами не заканчивается. Решение Эйлера было актуально на протяжении долгого времени, но в 1905 году все изменилось. Существует городская легенда, что на одном из светских приемов группа ученых решила подшутить над самим кайзером — императором Вильгельмом II. Тот пыхтел не один час в попытке решить головоломку, пока не включил императорскую смекалку. Так в Кенигсберге появился восьмой мост, который назвали, естественно, Императорским, а что стало с теми учеными-шутниками доподлинно не известно.
Увы, но восьмой мост был разрушен в ходе бомбардировки во время Второй мировой войны. На его опорах уже в 2005 году был построен Юбилейный мост, чье открытие приурочили к 750-летнему юбилею города.
Источник
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Загадка Эйнштейна — известная логическая задача, по легенде созданная Альбертом Эйнштейном в годы его детства. Также бытует мнение, что она использовалась Эйнштейном для проверки кандидатов в ассистенты на способность к логическому мышлению. Иногда автором головоломки называют Льюиса Кэрролла.
Некоторые приписывают Эйнштейну рассуждение, в котором тот утверждает, что лишь два процента населения земного шара способны оперировать в уме закономерностями, связанными сразу с пятью признаками. Как частное следствие этого, приведённая головоломка может быть решена без использования бумаги лишь теми, кто принадлежит к этим двум процентам.
В своём самом сложном варианте задача предполагает решение в уме, без использования каких-либо записей или средств сохранения информации. Без этих ограничений головоломка заметно теряет в сложности, поскольку может быть решена простым составлением таблицы с исключением заведомо противоречивых вариантов, и, следовательно, мало что говорит о способностях испытуемого.
Оригинальная задача Эйнштейна имеет два вопроса, но мы давайте попробуем ответить хотя бы на один:
5 разных человек в 5 разных домах разного цвета, курят 5 разных марок сигарет, выращивают 5 разных видов животных, пьют 5 разных видов напитков. Вопрос: кто выращивает рыбок?
1. Норвежец живет в первом доме.
2. Англичанин живет в красном доме.
3. Зеленый дом находится левее белого.
4. Датчанин пьет чай.
5. Тот, кто курит Rothmans, живет рядом с тем, кто выращивает кошек.
6. Тот, кто живет в желтом доме, курит Dunhill.
7. Немец курит Marlboro.
8. Тот, кто живет в центре, пьет молоко.
9. Сосед того, кто курит Rothmans, пьет воду.
10. Тот, кто курит Pall Mall, выращивает птиц.
11. Швед выращивает собак.
12. Норвежец живет рядом с синим домом.
13. Тот, кто выращивает лошадей, живет в синем доме.
14. Тот, кто курит Philip Morris, пьет пиво.
15. В зеленом доме пьют кофе.
Попробуйте решить эту задачку без бумажных записок.
А вот тут правильный ответ:
Итак, у нас есть 25 позиций, которые необходимо заполнить следующими данными:
- Национальность: Норвежец, Англичанин, Датчанин, Немец, Швед.
- Цвет дома: Красный, Зелёный, Белый, Жёлтый, Синий.
- Марка сигарет: Ротманс, Данхилл, Мальборо, Пелл Мелл, Филипп Моррис.
- Животное: Кошки, Птицы, Собаки, Лошади, Рыбки.
- Напиток: Чай, Молоко, Вода, Пиво, Кофе.
По сути, нам надо заполнить вот такую табличку:
Национальность
Цвет дома
Сигареты
Животное
Из подсказок сразу же заполняем ряд ячеек таблицы:
- Норвежец живет в первом доме.
- Норвежец живет рядом с синим домом.
- Тот, кто выращивает лошадей, живет в синем доме.
- Тот, кто живет в центре, пьет молоко.
Национальность
Цвет дома
Сигареты
Животное
Напиток
Раз англичанин живёт в красном доме, значит, норвежец в красном жить не может. Равно норвежец не может жить в синем. Не может он жить и в белом, так как зелёный дом находится левее белового, а дом норвежца — самый левый. В зелёном он тоже жить не может, так как справа от зелёного белый дом, а справа от норвежца — синий. Значит, он живёт в жёлтом. Отсюда же делаем и вывод, что норвежец курит Данхилл.
Национальность
Цвет дома
Сигареты
Животное
Напиток
Далее, раз зелёный дом находится левее белого, значит, у него номер либо 3, либо 4. Однако в третьем, среднем, доме пьют молоко, а в зелёном доме пьют кофе — значит номер зелёного дома = 4. Значит, белый дом у нас идёт под номером 5, а красный — под номером 3. Здесь же живёт англичанин. Кофе пьют в 4 доме.
Национальность
Цвет дома
Сигареты
Животное
Напиток
Далее, раз немец курит Мальборо, то он не курит Филипп Моррис, и потому не пьёт пиво. Не пьёт он и молоко, которое пьёт англичанин. Не пьёт и чай — это делает датчанин. Значит, немец пьёт либо воду, либо кофе. Норвежец не может пить пиво (он курит другие сигареты), молоко (не англичанин), кофе (живёт не в зелёном доме), чай (не датчанин). Значит норвежец пьёт воду, а потом немец пьёт кофе, и живёт в зелёном доме. Плюс не забываем, что немец курит Мальборо. И раз воду у нас пьёт норвежец, то его сосед (второй дом) курит Ротманс.
Национальность
Цвет дома
Сигареты
Животное
Напиток
Раз швед у нас выращивает собак, то он не может жить во втором доме (там выращивают лошадей), значит он живёт в пятом доме (белом). Значит во втором доме живёт датчанин, который пьёт чай.
Национальность
Цвет дома
Сигареты
Животное
Напиток
Раз курильщик Пелл Мелл выращивает птиц, то это не швед, а значит — англичанин. Следовательно, швед курит Филипп Моррис и пьёт пиво.
Национальность
Цвет дома
Сигареты
Животное
Напиток
И теперь у нас осталась последняя подсказка:
- Тот, кто курит Rothmans, живет рядом с тем, кто выращивает кошек.
Ротманс курит датчанин, что живёт во втором доме. Справа от него живёт англичанин, который выращивает птиц, значит, второй сосед датчанина (слева), норвежец, этих кошек и выращивает. А потом рыбок выращивает немец. Ответ найден.
Национальность
Цвет дома
Сигареты
Животное
Напиток
ОТВЕТ: НЕМЕЦ
Эйнштейн не указал как считать дома — со стороны прохожего, идущего по улице, либо человека, сидящего в одном из этих домов. В первом случае — зеленый это 4 дом, а белый 5. Во втором случае, если сидеть в окне белого дома, то зеленый тоже будет 4, но белый то будет 3 домом.. И ответом будет Англичанин.
Источник
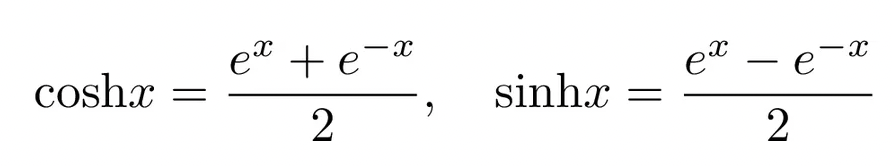
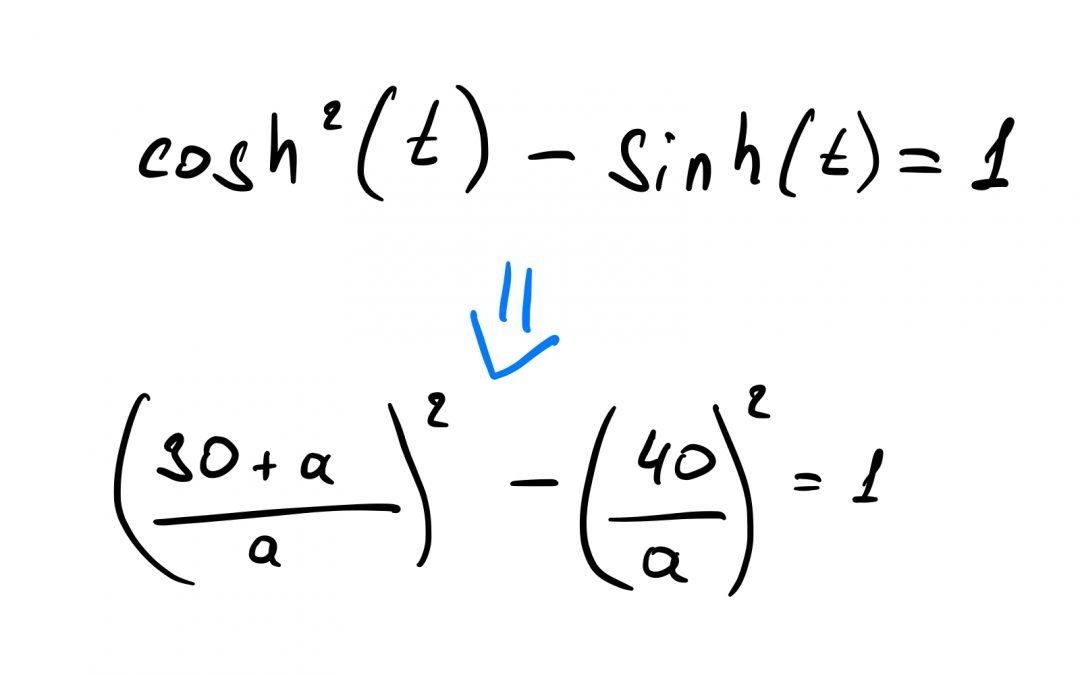
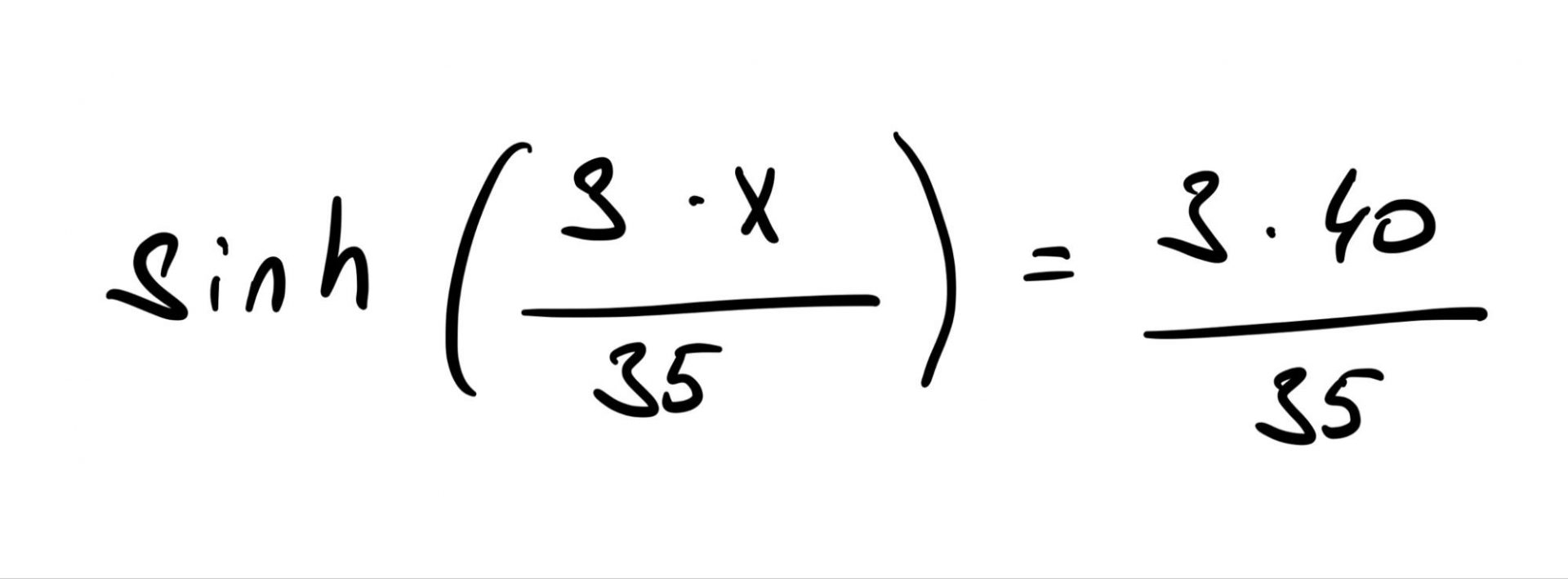





 masterok
masterok